今回の画像条件は以下のとおり。
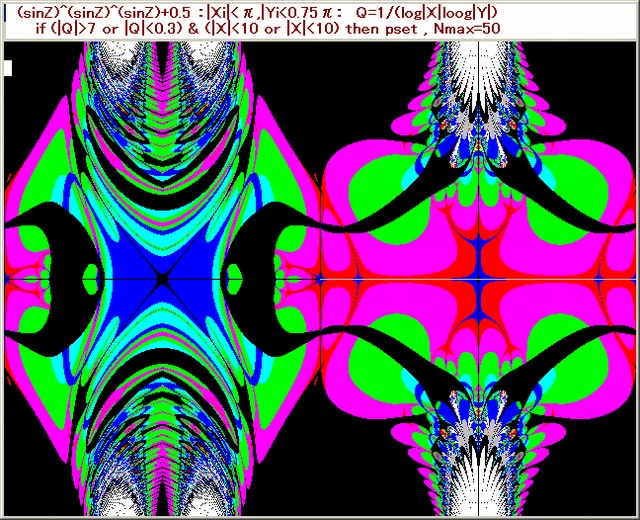
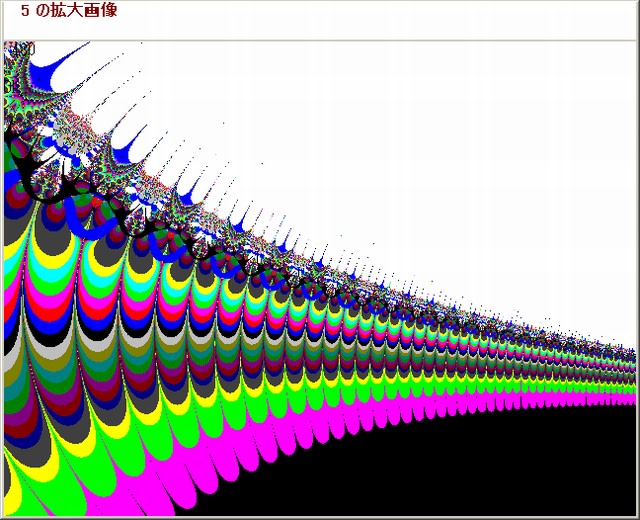
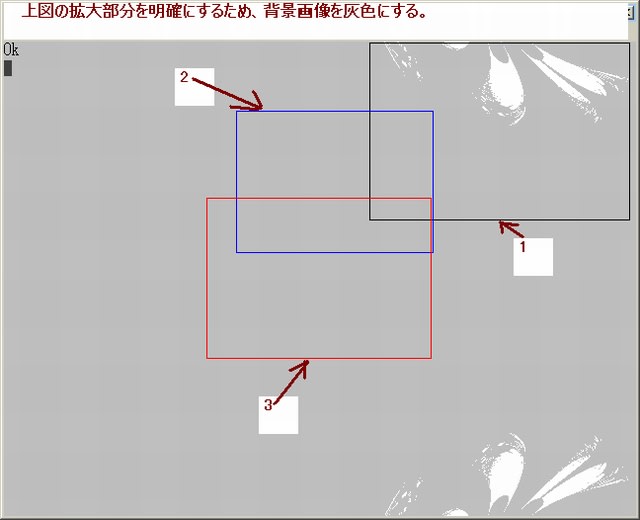
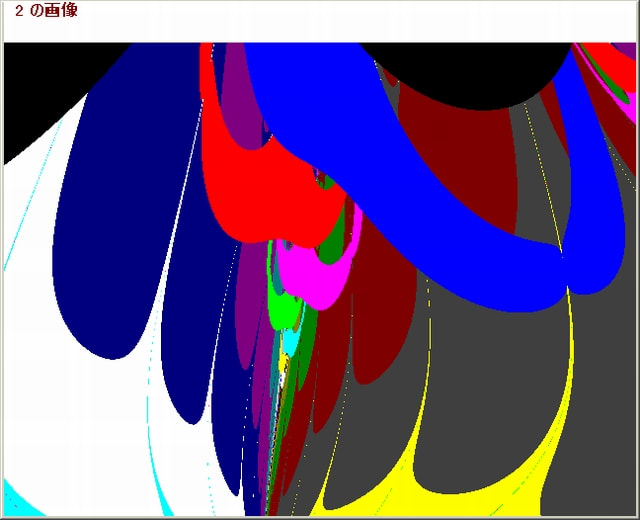
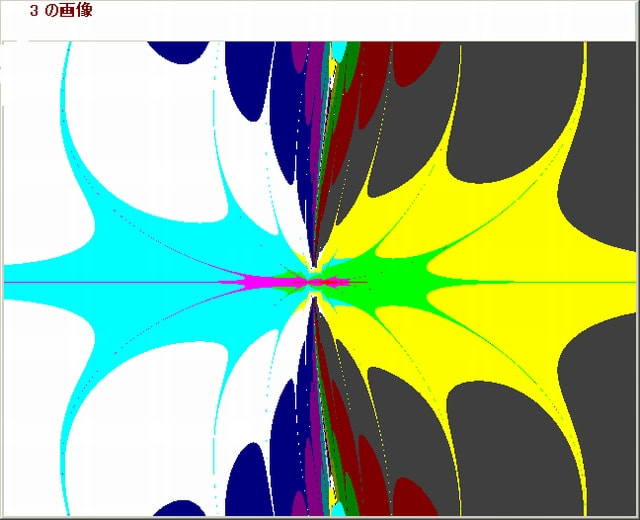
・複素関数:下図の上段左より、(e^sinZ)^sinZ^sinZ+0.5, (e^sinZ)^(e^sinZ)^sinZ+0.5, (e^sinZ)^(e^sinZ)^(e^sinZ)+0.5
下図の下段左より、(sinsinZ)^sinZ^sinZ+0.5, (sinsinZ)^(sinsinZ)^sinZ+0.5,(sinsinZ)^(sinsinZ)^(sinsinZ)+0.5
・N-loop脱出条件:Q=1/(log|X|log|Y|),(|Q|>7 or |Q|<0.3)
・pset条件:(|X|<10 or |Y|<10)
・θの与え方は方法3

・複素関数:下図の上段左より、(e^sinZ)^sinZ^sinZ+0.5, (e^sinZ)^(e^sinZ)^sinZ+0.5, (e^sinZ)^(e^sinZ)^(e^sinZ)+0.5
下図の下段左より、(sinsinZ)^sinZ^sinZ+0.5, (sinsinZ)^(sinsinZ)^sinZ+0.5,(sinsinZ)^(sinsinZ)^(sinsinZ)+0.5
・N-loop脱出条件:Q=1/(log|X|log|Y|),(|Q|>7 or |Q|<0.3)
・pset条件:(|X|<10 or |Y|<10)
・θの与え方は方法3