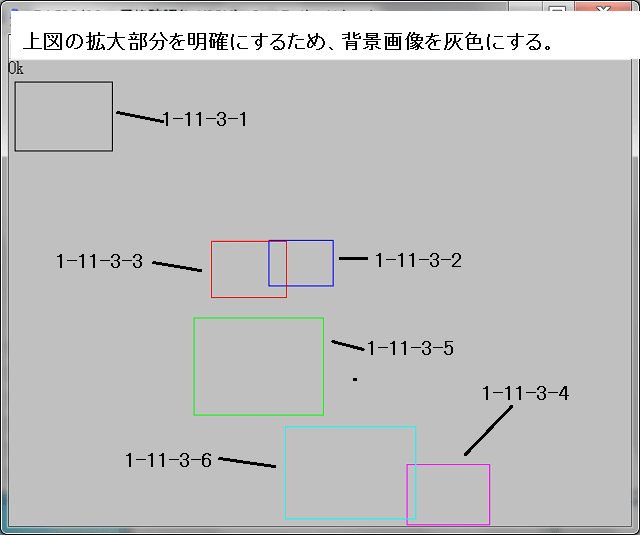
先ず、1-11-3の箇所を再確認する。



-----------------------------------------------
上図の1-11-3画像の6箇所(1-11-3-1~1-11-3-6)の部分を以下の2種類の画像処理を行い拡大する。
1.C=15-(4*log(No) MOD 16)
2.縞模様化:
縞模様は、N=Na以下→偶奇の縞模様とする。また、
Nb<N<Nc →C=4(緑)
Nc<N<Nd →C=9(暗い青)
N>=Nd →C=6(黄色)→Nmax=5000としているので、N-loop貫通部分を示す。
空白部分は、Na<N<Nb部分を示す。
-----------------------------------------------
・1-11-3-1 画像


・1-11-3-2 画像


・1-11-3-3 画像


・1-11-3-4 画像


・1-11-3-5 画像


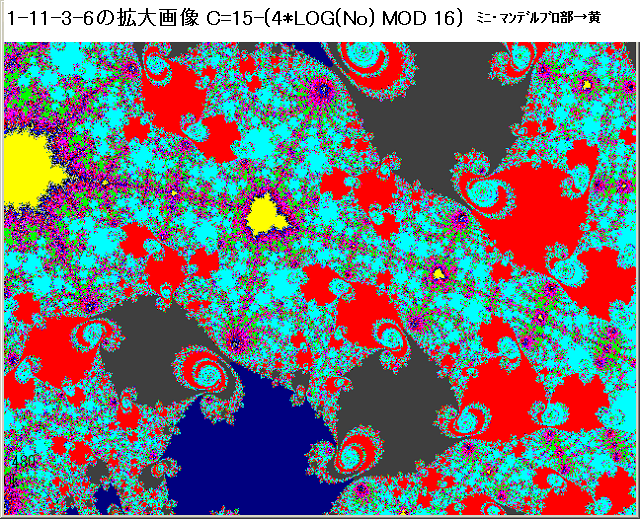
・1-11-3-6 画像





-----------------------------------------------
上図の1-11-3画像の6箇所(1-11-3-1~1-11-3-6)の部分を以下の2種類の画像処理を行い拡大する。
1.C=15-(4*log(No) MOD 16)
2.縞模様化:
縞模様は、N=Na以下→偶奇の縞模様とする。また、
Nb<N<Nc →C=4(緑)
Nc<N<Nd →C=9(暗い青)
N>=Nd →C=6(黄色)→Nmax=5000としているので、N-loop貫通部分を示す。
空白部分は、Na<N<Nb部分を示す。
-----------------------------------------------
・1-11-3-1 画像


・1-11-3-2 画像


・1-11-3-3 画像


・1-11-3-4 画像


・1-11-3-5 画像


・1-11-3-6 画像
































































































