アサルトアーマーRevenge/Part4

Part1レギュ1.30でのAA攻撃力計算に先立ち
Part216000≦PAのAA攻撃力式
Part312000≦PA≦16000のAA攻撃力式
Part49000≦PA≦12000のAA攻撃力式
Part5PA≦9000のAA攻撃力式
Part6AA攻撃力計算式まとめ
Part7PA満タン以外でも計算式を成立させる

Part4は9000≦PA≦12000のAA攻撃力についてです。流れはおそらく前回と全く一緒になるでしょう。PA12000に関する値はPart3の計算値を参照。

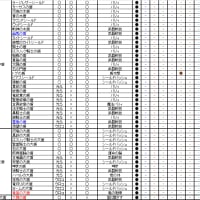
PA9000、10000、11000での総合AA攻撃力の実測値は、


総合AA攻撃力から算出したAA攻撃力は、


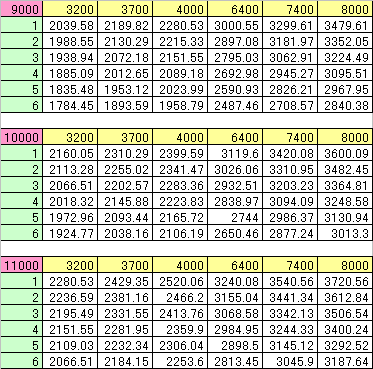
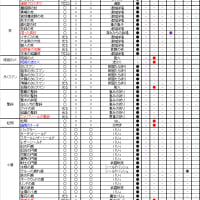
各AA攻撃力/OBについて、段数を変数とした近似直線の傾きと切片は、


傾きのグラフは、


切片のグラフは、


各近似直線から傾き-傾き、傾き-切片、切片-傾き、切片-切片を求める。PA12000の値は計算値から引用。


傾き-切片は0にする。

傾き-傾きのPAを変数とした近似式を求める。


傾き-傾き＝0.13244×10^(-5)×PA-0.027899と出たが、PA12000のときに、傾き-傾き＝-0.012という束縛条件がある。この近似式の切片を-0.012と同じ桁数の-0.028と補正してから、束縛条件に沿うようにあてはめると、近似式の傾きは以下のように求められる。
近似式の傾き×12000-0.028＝-0.012　より、
(-0.012+0.028)/12000＝2/15×10^(-5)≒0.13333×10^(-5)で近似直線の値におおむね合っている。
傾き-傾き＝2/15×10^(-5)×PA-0.028　とする。
また、(傾き-傾き)＋(切片-傾き)＝0.30である。

切片-切片について、


切片-切片＝0.12×PAと求められた。

以上から、9000≦PA≦12000において、
AA攻撃力＝[(Z-1){2/15×10^(-5)×PA-0.028}＋0.30]×AA＋0.12×PA

PA12000を除く、PA9000、10000、11000の計算値は、



計算値-実測値の平均絶対誤差は0.43887、最大絶対誤差は1.3446であり、1.34461＜1.41736であるため精度については問題ない。

よって、
AA攻撃力＝[(Z-1){2/15×10^(-5)×PA-0.028}＋0.30]×AA＋0.12×PA (9000≦PA≦12000)


Part5PA≦9000のAA攻撃力式です。