アサギマダラの渡りからヒントを得た滞空飛行２

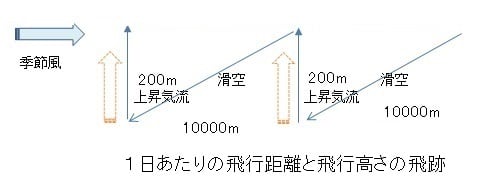
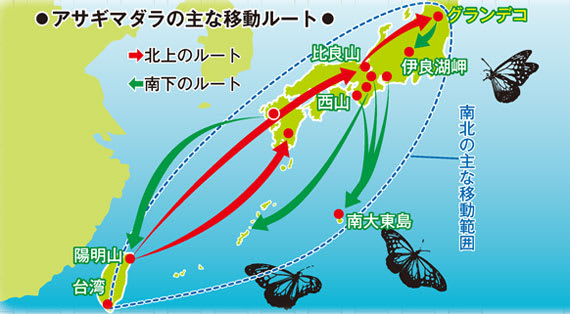
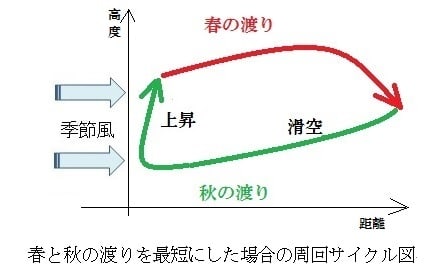
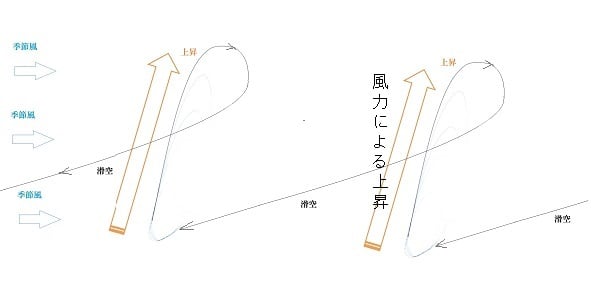
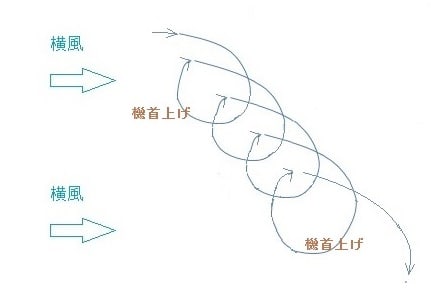
前回に続いて、サイクル滞空飛行の可能性について考える。
まず高度１５ｋｍ～２０ｋｍの成層圏において風上には滑空下降によって進み、
風下には機首上げをおこなって、揚力増加によって上昇するというサイクル飛行である。


機体重量３０ｋｇおよび５０ｋｇについてのサイクル飛行は３０ｍ/ｓ程度の風速では
落下前の元の高度まで戻ることができないため不可能であった。
　　　　　
サイクル飛行が成り立つための機体条件と空気流速を近似的に検証する。
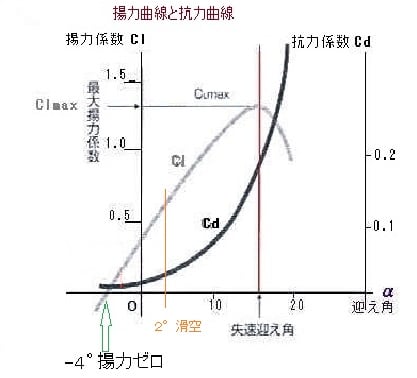
揚力係数Ｃ（Ｌ）＝１．０
抗力係数Ｃ（Ｄ）＝０．０２
成層圏内・風速２２(m/s)・翼面積２０(m2)・総重量１０ｋｇでの機体について
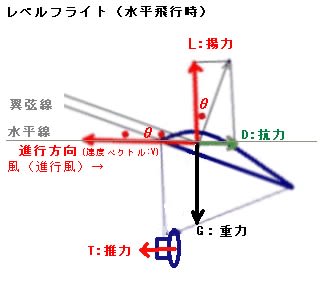
揚力Ｌは
Ｌ＝1/2{0.09(kg/m3)*22^2(m2/s2)*20(m2)*1.0}=435（Ｎ : kg.m/s2）

自由落下から滑空姿勢によって風上に進み、機首上げしたときに生ずるネットの揚力は、
抗力を無視できるくらい小さいとすれば上記揚力から重力を引いた上向きの成分で
435N－ｍ・ｇ＝435－10x9.8＝337N の揚力を受けて上昇する。
このときの運動方程式はｍ（ｄｔ２／ｄ２ｔ）＝Ｌ－ｍ・ｇ

物体に作用する力ＦはＦ＝ｍ・ａ質量に加速度をかけたものだからこの時の
加速度は　a＝337／10＝33．7（ｍ／ｓ２）

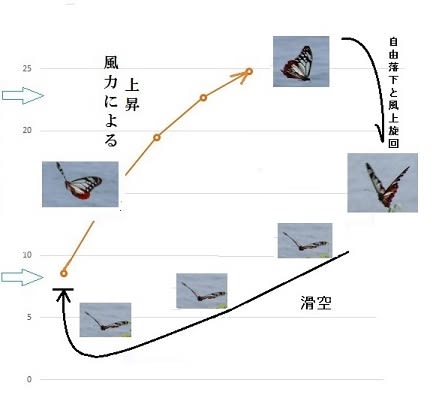
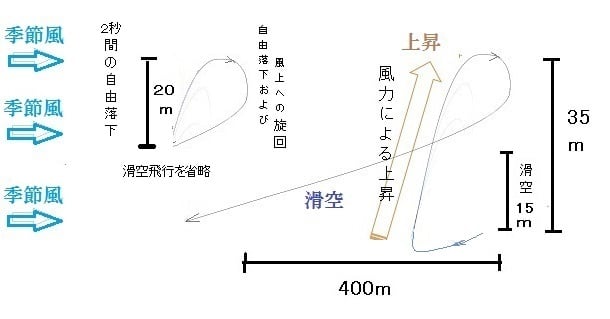
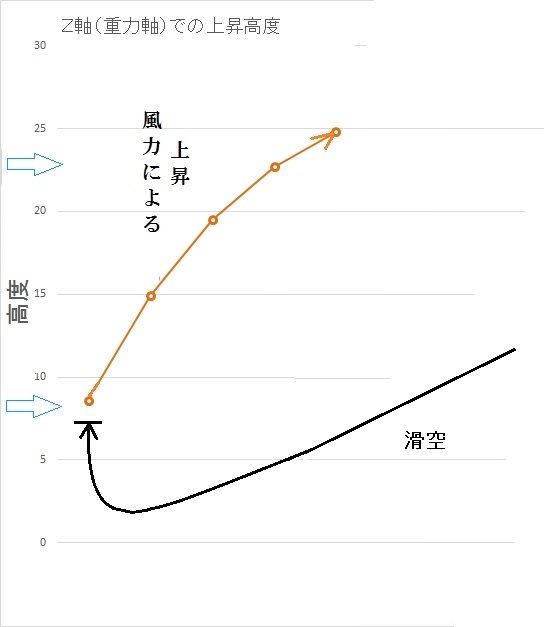
従って１秒後の上昇距離はｙ＝１／２（a・ｔ２）=16．8ｍ　となる。
次の１秒間は近似的に初速度（Ｖ0）16．8ｍ／ｓでの上昇で置き換えると、
初速度からの打ち上げで計算される上昇距離は、重力方向をマイナスとして
ｙ＝－１／２（ｇ・ｔ２）+Ｖ0・ｔ
から、－１／２（9.8ｘ１）+16．8＝11．9ｍの上昇となる。
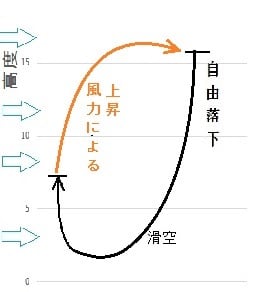
従ってトータル16．8+11．9＝28．7ｍの上昇である。
その後重力加速度の方が勝って、飛行体は落下する。
上昇した距離は28．7ｍで、近似所要時間は２秒間である。
　　　

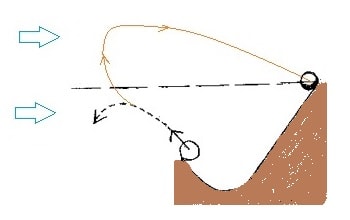
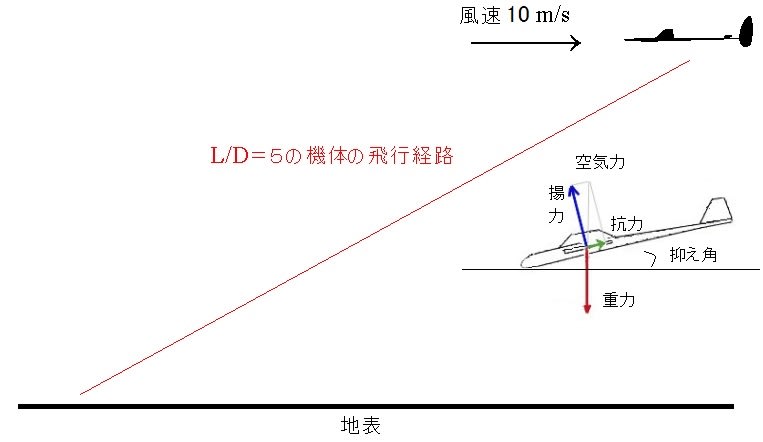
さて、上昇揚力がなくなれば落下が始まる。そのとき機体はほぼ風速２２(m/s)で
風下に流される状態となって落下している。従って横風で流される相対速度を
キャンセルするには、落下速度が最低でも２２ｍ/ｓとなることが必要である。
2.3秒間での落下速度は22．6ｍ/sなので、この速度で機首を風上に向ければ
地上から見たとき、風速２２(m/s)の横風での相対空気流揚力が得られたサイクル飛行が
可能となる。一方2.3秒間での自由落下距離は25．9ｍで上昇距離の方が大きいので、
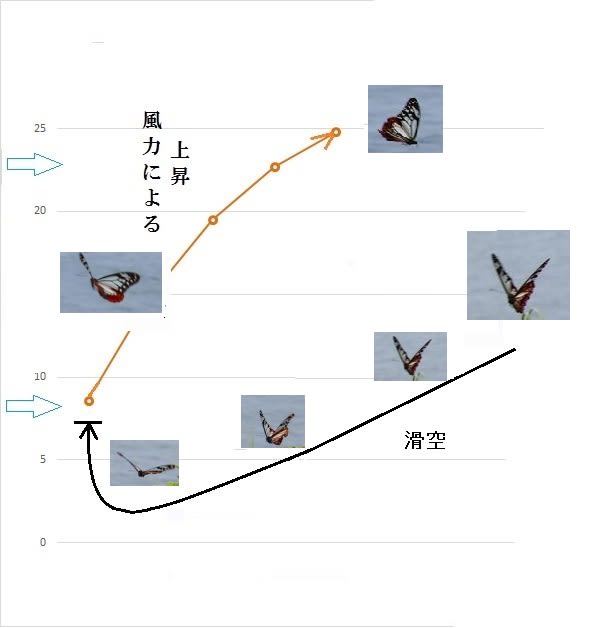
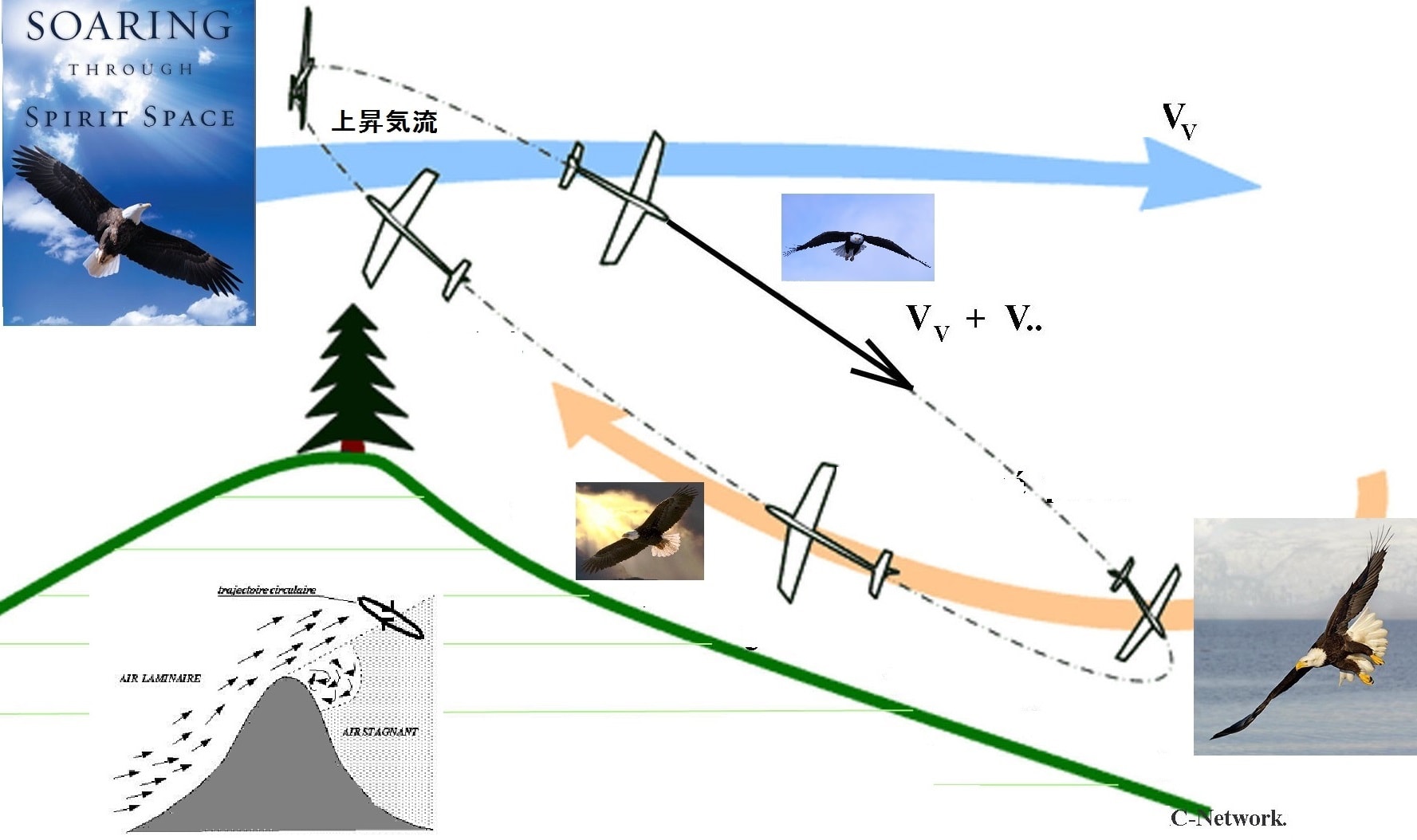
サイクル飛行を繰り返すことで、横風だけで徐々に高度を上げられる。下図
上記の状態が想定した重量ではサイクル飛行のためのミニマムであろう。
風速２２(m/s)以上の横風があれば上昇距離および自由落下時間ともに拡大した
サイクル飛行が可能となる。風速および機体の抗力が大きければそれだけ風下に
流される横方向の距離が大きくなる。
従って滞空維持には何サイクルか毎での風上への滑空飛行が必要となる。

　　　　　　　　　　　　　　サイクル飛行の概念図

ここでの問題はやはり重量である。翼面積２０(m2)・総重量１０ｋｇでの機体とするには
２ｍｘ５ｍの翼面積を５ｋｇで、２枚の複葉にして強度のある構造にしなければならない。
また、抗力係数が大きい場合には、揚力による上昇時間が短くなって、上昇距離が伸びない。
また風下への移動も大きくなって、その分頻繁に風上への滑空飛行が必要となる。
従って、サイクル飛行には軽量且つ抗力係数の小さな機体設計が不可欠となる。

成層圏のように、無尽蔵に風があり、尚且つ対流圏のような無風状態や乱気流の無い空域での
周回サイクル飛行が可能である。
上昇気流がない場合、風力エネルギーを利用した上昇飛行であって、
風力エネルギーを効率よく利用するためには、強風でも吹き飛ばされないように、
アサギマダラのように翼を立てて、自由落下に近づける。

アサギマダラの渡りからヒントを得た滞空飛行

アサギマダラの渡り
アサギマダラは渡りによって２，０００ｋｍもの距離を移動していることが知られている。
アサギマダラは昆虫であるが故、その渡りにおいては動力源が制限されている。
従って、上昇気流を使って上昇していると考えられている。
上昇の後には、滑空下降によって、下図のように風上への移動が可能となる。
その繰り返しで渡りを行う。





しかし上昇気流のない海をも渡ってくるので上昇気流だけでは説明が不十分だ。
そもそも１０ｋｍに一度の割合で上昇気流が無いと渡りができないとなれば、
秋の渡りにおいて、２、０００ｋｍもの距離を向かい風に向かって移動することは
不可能に近い。
ここで考えられるのは横風のみの風力エネルギーを利用した上昇飛行である。
滑空下降の途中で強い向かい風に遭遇したときに、翼の迎え角を大きく上げて、
揚力増大による上昇飛行を行うのである。何しろ揚力は相対気流速の二乗に比例して
増大するので、向かい風の強風は、上昇する時に大変効率的である。


従ってアサギマダラは翅面積の増大ではなく、強い風力エネルギーで高度を上げる
方法を選択し、翅を紙のように薄くし抗力を小さくすることで実現していると考えられる。
これが紙飛行機の様な蝶が動力もないのに、風力エネルギーによって２、０００ｋｍもの
距離を向かい風に向かって飛行する秘密である。

　　　　　　　　　　　　　　画面に向かって風が吹いている場合

アサギマダラの秋の渡りは上昇気流がなくても、風力エネルギーによっても上昇が
可能であることを教えている。
そうであれば成層圏のように、無尽蔵に風があり、尚且つ対流圏のような無風状態や
乱気流の無い空域での周回サイクル飛行が可能である。
一方滑空においては抗力を極力小さくすれば強風においても風上に進むことが可能で
加えて僅かな上昇移動であっても、風上への移動距離が長くなる。


そこでアサギマダラの渡りサイクルを短縮させれば、成層圏での滞空飛行が実現する。



上昇気流が無い場合の風上への移動飛行（秋の渡り）


下降によって風上の上昇位置に戻り、翼面積を広げて再上昇すれば滞空飛行となる。



尚、自由落下および風上に向かう旋回飛行の後、滑空は行わずに直ちに上昇すれば、
さらに短時間、狭い範囲での滞空サイクルの可能性さえある。（下図）
　　　　　　
推力と重力の合成力（Ｔ+Ｇ）より、揚力と抗力（Ｌ+Ｄ）の合成の方が大きい場合に
上昇する。風上に向かう推力は自由落下の運動エネルギーによって得られる。
　　　
モデル機体での滞空飛行の可能性について
翼の軽量化をはかり、２枚の複葉として翼面積２０ｍ２、総重量１０ｋｇ　
抗力係数：Ｃｄ＝0.04 および揚力係数：Ｃｌ＝1.0　とした場合、
高度２０ｋｍの成層圏において風速３０ｍ/s　気体密度０．０９(kg/m3)では、
揚力はＬ＝1/2[0.09x30^2x２０x1.0]=８１０ Ｎ( kg.m/s2）から、概略抗力と推力は
互いにキャンセルするので、自重分を差し引くと８１０N-(１０kgx9.8m/s2)=７１２N
となる。
これは１０kgの機体が７０ (m/s2）の加速度(a)で風下に上昇する力である。
一秒後の移動距離は1/2（a・ｔ＾２）=　３５mとなる。


滑空角はｔａｎθ＝Ｃｄ／Ｃｌ　　Ｃｄ＝0.04 Ｃｌ＝1.0の機体ではｔａｎθ＝0.04　なので　
tan-1(0.04／1.0）=0.04 から θ＝2.29と計算される。
滑空比Ｃｌ／Ｃｄ＝２５では、滑空しながら１０ｍ下降すれば横方向の移動距離は２５０ｍとなる。
また、滑空飛行においては、滑空速度Ｖは翼面積Ｓと翼面加重Ｗ／Ｓ（kg/m2）において
Ｖ＝４√（Ｗ／Ｓ）ｘ（１／√Ｃｌ）（m/s）である。
成層圏での相対風速３０m/sにおいて、上記機体は約１秒で風下へ約３５ｍ上昇し、
自由落下２秒、２０ｍの落下の後、相対速度を得て旋回飛行し、風上へ向かいながら
滑空下降で１５ｍの下降、このとき風上への移動移動はおよそ４００ｍの移動となる。
滞空時間サイクルは上昇が１秒、自由落下２秒、滑空が２．４分での滞空である。



翼面積２０ｍ２、総重量１０ｋｇ　では翼駆動機構や通信機搭載の実用機体では
相当にハードルが高い。サイクル滞空飛行については後日
また、総重量を増やすにはスケールメリットを活かすしかなく、飛行船と同様に
巨大化につながり、耐久構造部分においても重量との闘いとなる。
最近電動飛行機の開発が盛んに行われているため、当機体の駆動機構の
軽量化にも応用が可能であって、特に炭素繊維強化プラスチックは
高い強度と軽さを併せ持つ材料のため、航空機などの産業用に用途が
拡大しており安価・軽量・高耐久性に期待が持てる。

アサギマダラの秋の渡り

季節風に向かって、２０００ｋｍも移動する紙飛行機の様なチョウ・・・謎の解明のために


従来の秋の渡りについて、上図の様な説明がされていた。
ここのブログでは上昇気流がなくても、向かい風さえあれば上昇できるポイントについて紹介する。
一旦上昇できれば、後は滑空しながら、風上に下降して移動する（位置エネルギーの放出）





滑空から、迎え角を上げて、風力により上昇する
風に吹き飛ばされないように、薄い翅を精確に風上に向ける

燃料なしでの地球一周空の旅

太陽エネルギーだけで飛ぶプロペラソーラープレーン、地球一周の旅へ出発


ジャンボッジェットと同じ大きさなのに搭乗者はパイロットただ一人だ。
無着陸飛行は最大５日間、操縦席の隣にベットとトイレがあって、酸素吸入器によって
呼吸を維持する。まるで寝たきり人間扱いだ。操縦席にエアコンはなく気温は
＋４０°C～－４０°Cと過酷な環境にある。しかし地上にいるヘルパーさんは６０人もいて、
とびっきりゴージャスだ。
「乗ってもいいよ」と勧められても、とても自信はなく私ならばごめんこうむる。
将来ソーラーバッテリーは改良されるだろうが、有人飛行としての展望は困難であろう。



　　　　　　　
speed of 49 knots (56.4 mph) at sea level.
This picks up to 77 knots (88.5 mph) at 27,000 feet, the craft’s maximum altitude
ジャンボジェット機と翼長は同じであって、離着陸も含め風には弱いため、
飛行可能な気象条件を選んで飛行しなければならず、世界一周には５か月程かかる。
最大飛行高度は２７、０００フィート（９ｋｍ）とあって、旅客機と同じかやや低い高度を飛ぶ。
飛行推進動力は夜間飛行の為に充電を優先して使う。従って風に逆らっての飛行は考えられない。
そうであればやはり風任せの飛行で、その点での現行機は気球と大して変わりない。






一方、気球による世界一周の飛行期間は２２日だが、基本的には風任せの飛行であって、
しかも季節風は季節によって大きく移動変動するから、着陸地は予定より外れる場合がある。
風任せの点では同じだが、実用的には高高度での飛行、コスト、搭載重量の点で将来展望は
ソーラープレーンより優位にあるように思う。
　　　　グーグル気球

JAXAでの実験は機器の回収を行うため、気球が放球後、風に乗って戻ってくるのは夏期だけで、
それ以外は実験できないのだそうだ。従って今の季節は、南半球に出かけて実験するのだそうだ。
それはそれで楽しそうだ。

アサギマダラが教える飛行思想

アサギマダラの渡りが教える飛行思想
　滑空による風上移動距離は、揚抗比の改善のみならず、高度を上げることでも伸ばすことができる。アサギマダラは昆虫であるが故、その渡りにおいては動力源が制限されているので、上昇気流を使って上昇していると考えられている。しかし上昇気流のない海をも渡ってくるので上昇気流だけでは不十分で、強い風を利用した上昇飛行も考えられる。従ってアサギマダラは翼面積の増大ではなく、強い風力エネルギーで高度を上げる方法を選択し、翼を紙のように薄くし抗力を小さくすることで実現していると考えられる。それが紙飛行機の様なチョウが、推進動力もないのに季節風に向かって２０００ｋｍもの距離を渡るエコ飛行の秘密である。

アサギマダラの渡りが教える機体構造思想
　揚力や抗力は相対気体流速度の二乗と翼面積に比例した力になる。従って強風下でも飛行できるコンパクトな機体にすれば、特段に翼面積を大きくしなくても同じ揚力が得られるし、抗力も小さくできる。推進動力を効率化するために翼面積を大きくしたり、グライダーのように高アスペクト比の長い翼としたりする機体設計もあるが、機体重量と機体強度との戦いと、風に弱くなるという欠点がある。アサギマダラの思想は強い風力エネルギーを利用するので、吹き飛ばされないように紙のように薄くて、コンパクトな設計である。しかし揚力の増大ではなく、抗力の最小化の方を選んだことで、こちらは無風状態では落下してしまうというリスクを負う。
　今の航空機は大気圏での飛行のために翼面積を大きくする設計である。その分抗力も大きくなって強風が吹くと欠航となる。しかしアサギマダラは強い風が吹くほど逆に有利である。
地上に近い対流圏では無風状態が存在するが、上空１５０００m付近の成層圏では、逆に上昇気流は期待できないけれど、無風状態の無い年中強風領域となっている。従ってアサギマダラにとって成層圏での飛行は不可能だが、そこの領域に限定した飛行機は、揚力が小さくても落下し続けることはなく、長期間の安定した滞空が実現できると考える。



　　　　　　
　　　強風を利用する思想　　　翼面積を利用する思想

　繁殖のためとはいえ強風に吹き飛ばされず、逆に強い季節風に突き進むための構造で、しかもそのための動力を使っている気配さえない。
つまり羽ばたきによって強風に立ち向かうのではなく、強風で得られる揚力により上昇し、その位置エネルギー使って風上に移動しているのである。
何億年もの自然環境のもとで淘汰され続け、そこで生き残った生き物には全くといって無駄なところがないとつくづく感じ入ってしまう。
戦闘機の設計も無駄なところは徹底して切り取る設計であろうから、期せずして最新戦闘機の正面から見た構造はアサギマダラとそっくりであった。

　　　　　

アサギマダラの滑空

ＮＨＫ-TV番組「ダーウインが来た」（２０１５年１月１１日）より。
日本列島２０００ｋｍを春と秋に縦断するチョウ（アサギマダラ）の生態
　　

番組では「NHKのマーキング作業によって春には一日で風下に向けて８０ｋｍ移動すること、
秋には７３日かけて風上に１４２０ｋｍ移動したことが確認された。」とあった。




そこでアサギマダラの生態から定点滞空飛行の可能性について検討してみた。

風上に向かって下降し、風下に向かって上昇しているので「ソアリング」と呼ばれる飛行とは
逆の飛行である。アサギマダラの場合は上昇気流に乗って上昇しているとのことである。
季節による風の強さ、方向、高度などの条件と、上昇気流の存在が必須であるからそれらの
条件によって滞空の範囲は異なるであろう。



ところでチョウの飛行姿を見ると（下図）翼の断面は紙のように薄い。

これは抗力が非常に小さいことを示している。滑空比は揚力と抗力の比によって決まるから
グライダーの５０よりは大きな値であることはこの写真から容易に想像される。
仮に滑空比８０とすれば、１００ｍの下降で風上には８０００ｍ進むことができる。
上昇気流によって１００ｍ上昇するのはチョウにとっても十分に現実味のある数字である。
チョウは十分に軽量なので、一旦上昇気流に乗れば、上昇のためのエネルギー消費はほとんど
ない状態でこの飛行が可能である。
一方、風上への飛行は滑空を使う。無動力のグライダーが飛行するように、位置エネルギーの
放出で飛行するため、エネルギー消費はない。
２０００ｋｍ程の飛行をすると聞くと、相当量のエネルギーが必要と思われるのだが、実際には
上昇気流さえ見つけられれば、チョウにとってほとんどエネルギーの消費はないことが分かる。

　　　　　　　滑空飛行のアサギマダラ　

さて番組によれば、風上には７３日かけて１４２０ｋｍの距離を滑空しながら進んだとある。
よって、一日あたりの移動距離はおよそ２０ｋｍである。
また風下には２４時間で８０ｋｍであるから、６時間で２０ｋｍの移動である。
従って風下に６時間の上昇飛行と空気流一体での飛行をし、風上には２４時間飛行で、
滑空下降のサイクルとすれば、それを反復することで、およそ２０ｋｍの範囲でエネルギー
消費無しに、定点滞空の可能性がある。

一方、上昇と下降の反復サイクルは、上昇気流による上昇高度と、滑空比による下降移動に
よって変化する。今仮に滑空比８０と仮定し、一回当たりの上昇高度が１２０ｍで、尚且つ、
水平移動距離の範囲を２０ｋｍ以内とした場合では、２回の滑空が必要であるから、その間で
２回の上昇が必要となる。１回あたりの上昇高度が高いほど、上昇サイクルは少なくなる。
従って上昇高度によって、上昇下降のサイクル回数が決まる。

アサギマダラの渡り条件下での上昇と下降の反復滞空サイクル
風下移動は６時間、風上滑空移動の方では２４時間のインタバルサイクル


チョウのような軽量動物だけが、こうした飛行が可能なのかもしれない。
しかしアサギマダラの渡りが教えてくれるのは、紙飛行機のような昆虫が、僅かなエネルギーで
季節風に向かって１０００ｋｍ以上も移動することが可能であるという事だ。
鳥類でも渡り鳥のように長距離を移動する動物が知られている。アサギマダラと同様に、
上昇気流と滑空を使っての飛行をすればエネルギーの消費は少なくて済みそうであるが、
チョウとは違い重量があるため、上昇気流に乗るまでには相当量のエネルギーは必要と
思われる。

　　

渡り鳥の場合はエネルギーを蓄える特殊な生化学反応を使っていると聞く。
エネルギー消費が少なくて、且つ上昇気流のない成層圏での滞空飛行を実現する
ためには、チョウのように抗力が少なく、且つ揚力は十分大きい薄断面翼を
持った構造が必須であろう。
写真右から分かるようにチョウは全翼機構造で、且つ複葉（４枚翼）となっていて、
長距離飛行にとって全く無駄のない構造だ。正しく自然の姿は理想的で美しい。

高度１５ｋｍ、偏西風による飛行機体揚力の計算例

高度１５ｋｍ、毎秒２０ｍの偏西風（ジェット気流）がある環境で
風上と風下を往復するときの仕事量。　　

［１］滑空下降時の計算



高度１５ｋｍ流体の密度：０.０９ kg/m3
翼面積：１５ｍ＊２ｍ＝３０ｍ２
翼と流体の相対的迎え角：２°
翼と流体の相対速度：２０ｍ／ｓ
揚力係数と抗力係数は下に示す例示グラフより
Ｃ（Ｌ）＝０．７
Ｃ（Ｄ）＝０．０２

であるから揚力は
Ｌ＝1/2{0.09(kg/m3)*20^2(m2/s2)*30(m2)*0.7}=３７８（Ｎ : kg.m/s2）
抗力は
Ｄ＝１０．８（Ｎ : kg.m/s2）

滑空比は揚抗比（３７８／１１）に等しい。
滑空飛行可能重量は３８ kg／COS（θ）≒３８ kg

１０N＝１ｋｇｘ１ｍの仕事量であるから
上記の揚力は３７．８ｋｇの重量物が１ｍ上昇移動する仕事量である。
このときの揚力が働く方向は風上で、重力と揚力の合成方向に進行する。

重力と揚力の合成方向は抗力と同等なので、このエネルギーが風上に向かう
エネルギーである。
抗力Ｄ＝１０．８（Ｎ : kg.m/s2）は３７．８ｋｇの重量物が移動する量
として換算してみると、０．０２８ｍとなる。従って毎秒２．８ｃｍ下降
しながら風上に向かって滑空する。




［２］翼の迎え角を増加した後の機体上昇の計算



翼面積：３０ｍ２
迎え角：１５°（最大値：失速の直前）
翼と流体の相対速度：２０ｍ／ｓ
揚力係数
Ｃ（Ｌ）＝１．３
Ｃ（Ｄ）＝０．１７


Ｌ＝７０２（Ｎ）となるから、重力分を差し引いた残りが上昇分となる。
７０２－３７８＝３２４（Ｎ）
差引３２４（Ｎ）／COS（１５°）≒３３７は、
３７．８ｋｇの重量物が一秒間に０．８９ｍ風下に上昇する仕事量である。
従って０．８９／０．０２８＝３１．８秒の滑空時間内であれば、
風速２０ｍ／ｓの偏西風が吹いている限り、推進動力を持たなくても
飛行機体の一定範囲内での長期間の滞空が可能である。

飛行機体の揚力計算例

毎秒１０ｍの横風がある環境で、風上と風下を往復するときの仕事量。　　

［１］滑空下降時の計算



流体の密度：海面高度の大気中なら 1.2 kg/m3
翼面積：６ｍ＊２ｍ＝1２ｍ２
翼と流体の相対的迎え角：２°
翼と流体の相対速度：１０ｍ／ｓ
揚力係数と抗力係数は下に示す例示グラフより
Ｃ（Ｌ）＝０．７
Ｃ（Ｄ）＝０．０２

であるから揚力は
Ｌ＝1/2{1.2(kg/m3)*10^2(m2/s2)*12(m2)*0.7}=５０４（Ｎ : kg.m/s2）
抗力は
Ｄ＝１４（Ｎ : kg.m/s2）

滑空比は揚抗比（５０４／１４）に等しい。
飛行可能重量は５０ kg／COS（θ）≒５０ kg
このときの揚力が働く方向は風上である。

一方必要動力は抗力分で１４ｘ１０＝１４０W
風力よる揚力が、風上に向かう分のエネルギーを供給する。
ポテンシャルエネルギー（ｍｇｈ）換算では、５０ｋｇの機体の場合
毎秒０．２８ｍの高度変化するエネルギーである。
１０秒間の滑空では、５０ｋｇの機体は２．８ｍの高度差となる。

ここでの滑空は、動力がなくてもグライダーのように自重によって毎秒
０．２８ｍ分のポテンシャルエネルギーを放出しながら風上へ下降する。



［２］翼の迎え角を増加した後の機体上昇の計算



翼面積：１２ｍ２
迎え角：１５°（最大値：失速の直前）
翼と流体の相対速度：１０ｍ／ｓ
揚力係数
Ｃ（Ｌ）＝１．３
Ｃ（Ｄ）＝０．１７


このとき揚力と抗力の合成力が働く方向は風下である。
揚力は風向きに対して垂直に働き、その量は
Ｌ＝９３６（Ｎ）となるから、重力バランス分を差し引いた残りが上昇分となる。
９３６－５０４＝４３２（Ｎ）
差引４３２（Ｎ）／COS（１５°）≒４５０は、５０ｋｇの機体が1秒間に0．9ｍ
風下に上昇するエネルギーに相当する。
およそ３秒間の滑空で下降したポテンシャルエネルギーに換算される。


飛行機体の一定範囲内での長時間滞空方法が可能である。

動力を持たない飛行機体の一定範囲内での長時間滞空方法（１）

パラグライダーのように動力を持たない飛行機体が、横風だけである一定の範囲を
維持しながら滞空時間を長くしようとすると、風下だけでなく風上にも進まなければ
ならない。そこで風上に進む場合には、翼形状を持つ機体として滑空を利用する。

揚力と機体重量とのバランスのほかに、風上に向かう場合は抗力が生じるから、
それを打ち消して、尚且つ風上に進むようにするには、揚力ベクトルを前傾にして
前に進める。即ち揚力は風向きに対して垂直に作用するので下降しながら前進する
ことになる。
このときの揚力と抗力の合成力は空気力と呼ばれていて、重量とバランスして
いれば風上に向かっての滞空時間は長くなる。
十分な滞空時間が得られれば、僅かに空気力を前傾させること、即ち滑空比を
大きくすることで、風上に前進させながら、ゆっくりと滑空させる。
風下に戻る場合は、翼を回転させて、一気に揚力を上げて、機体を上昇させ
ながら、機体を相対空気流がなくなるまで風下に戻す。
そこから再度滑空を繰り返すことで、動力を持たない飛行機体の一定範囲内での
長時間滞空方法が可能である。






写真のような動力のないパラグライダーでは、風によって風下に移動して
しまうために、決まった位置での長時間滞空ができない。しかしコストをかければ
太陽光による動力で、一機２億円程度で長時間滞空法が実現されている。

ソアリング航法とは

Soaring（ソアリング）航法とは

グライダーが上昇気流によって高度または速度を増加する航法。
上昇気流のある風上に向かい上昇し、そこから下降することでの
位置エネルギーを運動エネルギーに変換し、そのスピードで再上昇する。

抗力で失った運動エネルギーを上昇気流で補完し、反復継続させ
滞空時間を長くする。









上昇気流がなくても、風力のみで滞空時間を長くする航法
滑空時
　　



上昇気流ではなく横風の向かい風に向かって滑空下降し、スイングバイにより上昇する。
揚力重力比が１になるまで上昇し、相対空気流がゼロになるまで風下に流されながら移動する。
そこからは、元の相対空気流を回復するまで自由落下によって加速し、元の揚力が得られたら、
基準高度で風上に向きを変え、重心移動により再滑空を始める。この動作を繰り返す。
滑空比が大きいほど、ゆったりとした飛行が可能である。



上昇時