高度１５ｋｍ、偏西風による飛行機体揚力の計算例

高度１５ｋｍ、毎秒２０ｍの偏西風（ジェット気流）がある環境で
風上と風下を往復するときの仕事量。　　

［１］滑空下降時の計算



高度１５ｋｍ流体の密度：０.０９ kg/m3
翼面積：１５ｍ＊２ｍ＝３０ｍ２
翼と流体の相対的迎え角：２°
翼と流体の相対速度：２０ｍ／ｓ
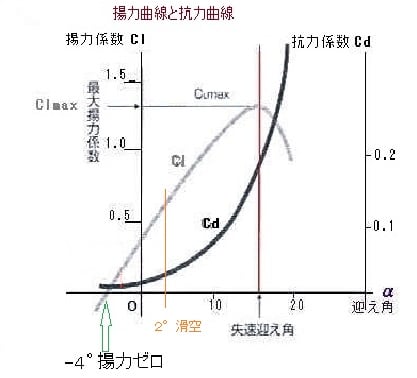
揚力係数と抗力係数は下に示す例示グラフより
Ｃ（Ｌ）＝０．７
Ｃ（Ｄ）＝０．０２

であるから揚力は
Ｌ＝1/2{0.09(kg/m3)*20^2(m2/s2)*30(m2)*0.7}=３７８（Ｎ : kg.m/s2）
抗力は
Ｄ＝１０．８（Ｎ : kg.m/s2）

滑空比は揚抗比（３７８／１１）に等しい。
滑空飛行可能重量は３８ kg／COS（θ）≒３８ kg

１０N＝１ｋｇｘ１ｍの仕事量であるから
上記の揚力は３７．８ｋｇの重量物が１ｍ上昇移動する仕事量である。
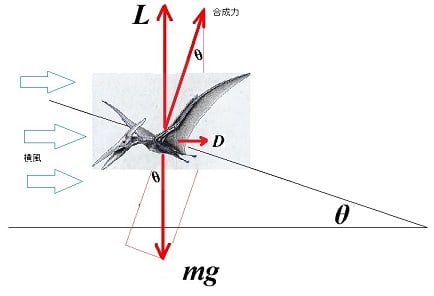
このときの揚力が働く方向は風上で、重力と揚力の合成方向に進行する。

重力と揚力の合成方向は抗力と同等なので、このエネルギーが風上に向かう
エネルギーである。
抗力Ｄ＝１０．８（Ｎ : kg.m/s2）は３７．８ｋｇの重量物が移動する量
として換算してみると、０．０２８ｍとなる。従って毎秒２．８ｃｍ下降
しながら風上に向かって滑空する。




［２］翼の迎え角を増加した後の機体上昇の計算



翼面積：３０ｍ２
迎え角：１５°（最大値：失速の直前）
翼と流体の相対速度：２０ｍ／ｓ
揚力係数
Ｃ（Ｌ）＝１．３
Ｃ（Ｄ）＝０．１７


Ｌ＝７０２（Ｎ）となるから、重力分を差し引いた残りが上昇分となる。
７０２－３７８＝３２４（Ｎ）
差引３２４（Ｎ）／COS（１５°）≒３３７は、
３７．８ｋｇの重量物が一秒間に０．８９ｍ風下に上昇する仕事量である。
従って０．８９／０．０２８＝３１．８秒の滑空時間内であれば、
風速２０ｍ／ｓの偏西風が吹いている限り、推進動力を持たなくても
飛行機体の一定範囲内での長期間の滞空が可能である。

飛行機体の揚力計算例

毎秒１０ｍの横風がある環境で、風上と風下を往復するときの仕事量。　　

［１］滑空下降時の計算



流体の密度：海面高度の大気中なら 1.2 kg/m3
翼面積：６ｍ＊２ｍ＝1２ｍ２
翼と流体の相対的迎え角：２°
翼と流体の相対速度：１０ｍ／ｓ
揚力係数と抗力係数は下に示す例示グラフより
Ｃ（Ｌ）＝０．７
Ｃ（Ｄ）＝０．０２

であるから揚力は
Ｌ＝1/2{1.2(kg/m3)*10^2(m2/s2)*12(m2)*0.7}=５０４（Ｎ : kg.m/s2）
抗力は
Ｄ＝１４（Ｎ : kg.m/s2）

滑空比は揚抗比（５０４／１４）に等しい。
飛行可能重量は５０ kg／COS（θ）≒５０ kg
このときの揚力が働く方向は風上である。

一方必要動力は抗力分で１４ｘ１０＝１４０W
風力よる揚力が、風上に向かう分のエネルギーを供給する。
ポテンシャルエネルギー（ｍｇｈ）換算では、５０ｋｇの機体の場合
毎秒０．２８ｍの高度変化するエネルギーである。
１０秒間の滑空では、５０ｋｇの機体は２．８ｍの高度差となる。

ここでの滑空は、動力がなくてもグライダーのように自重によって毎秒
０．２８ｍ分のポテンシャルエネルギーを放出しながら風上へ下降する。



［２］翼の迎え角を増加した後の機体上昇の計算



翼面積：１２ｍ２
迎え角：１５°（最大値：失速の直前）
翼と流体の相対速度：１０ｍ／ｓ
揚力係数
Ｃ（Ｌ）＝１．３
Ｃ（Ｄ）＝０．１７


このとき揚力と抗力の合成力が働く方向は風下である。
揚力は風向きに対して垂直に働き、その量は
Ｌ＝９３６（Ｎ）となるから、重力バランス分を差し引いた残りが上昇分となる。
９３６－５０４＝４３２（Ｎ）
差引４３２（Ｎ）／COS（１５°）≒４５０は、５０ｋｇの機体が1秒間に0．9ｍ
風下に上昇するエネルギーに相当する。
およそ３秒間の滑空で下降したポテンシャルエネルギーに換算される。


飛行機体の一定範囲内での長時間滞空方法が可能である。