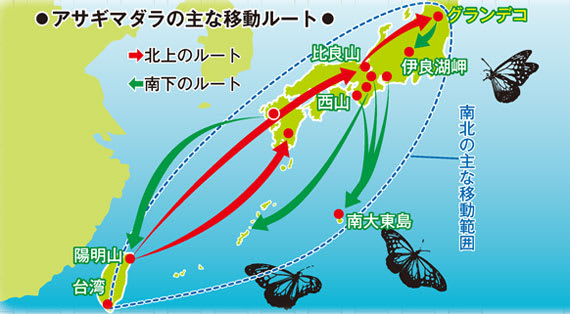
アサギマダラの渡り
アサギマダラは渡りによって2,000kmもの距離を移動していることが知られている。
アサギマダラは昆虫であるが故、その渡りにおいては動力源が制限されている。
従って、上昇気流を使って上昇していると考えられている。
上昇の後には、滑空下降によって、下図のように風上への移動が可能となる。
その繰り返しで渡りを行う。
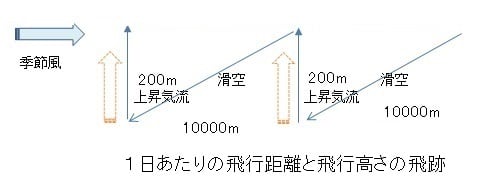
しかし上昇気流のない海をも渡ってくるので上昇気流だけでは説明が不十分だ。
そもそも10kmに一度の割合で上昇気流が無いと渡りができないとなれば、
秋の渡りにおいて、2、000kmもの距離を向かい風に向かって移動することは
不可能に近い。
ここで考えられるのは横風のみの風力エネルギーを利用した上昇飛行である。
滑空下降の途中で強い向かい風に遭遇したときに、翼の迎え角を大きく上げて、
揚力増大による上昇飛行を行うのである。何しろ揚力は相対気流速の二乗に比例して
増大するので、向かい風の強風は、上昇する時に大変効率的である。
従ってアサギマダラは翅面積の増大ではなく、強い風力エネルギーで高度を上げる
方法を選択し、翅を紙のように薄くし抗力を小さくすることで実現していると考えられる。
これが紙飛行機の様な蝶が動力もないのに、風力エネルギーによって2、000kmもの
距離を向かい風に向かって飛行する秘密である。

画面に向かって風が吹いている場合
アサギマダラの秋の渡りは上昇気流がなくても、風力エネルギーによっても上昇が
可能であることを教えている。
そうであれば成層圏のように、無尽蔵に風があり、尚且つ対流圏のような無風状態や
乱気流の無い空域での周回サイクル飛行が可能である。
一方滑空においては抗力を極力小さくすれば強風においても風上に進むことが可能で
加えて僅かな上昇移動であっても、風上への移動距離が長くなる。
そこでアサギマダラの渡りサイクルを短縮させれば、成層圏での滞空飛行が実現する。
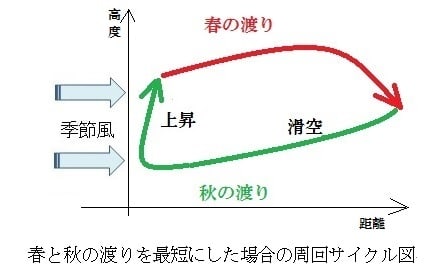
上昇気流が無い場合の風上への移動飛行(秋の渡り)
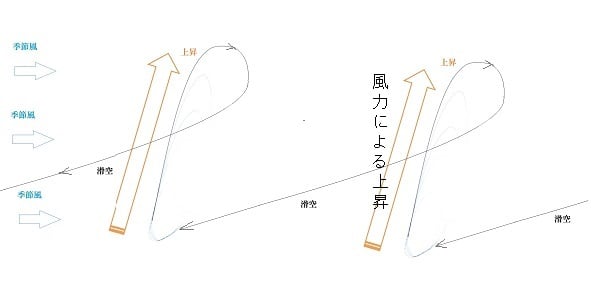
下降によって風上の上昇位置に戻り、翼面積を広げて再上昇すれば滞空飛行となる。
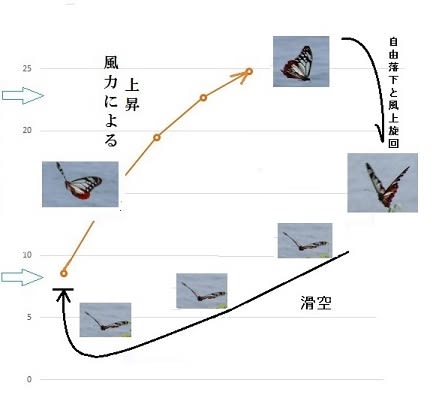
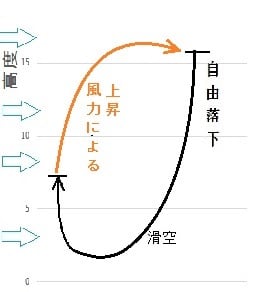
尚、自由落下および風上に向かう旋回飛行の後、滑空は行わずに直ちに上昇すれば、
さらに短時間、狭い範囲での滞空サイクルの可能性さえある。(下図)
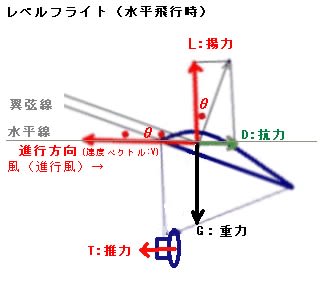
推力と重力の合成力(T+G)より、揚力と抗力(L+D)の合成の方が大きい場合に
上昇する。風上に向かう推力は自由落下の運動エネルギーによって得られる。
モデル機体での滞空飛行の可能性について
翼の軽量化をはかり、2枚の複葉として翼面積20m2、総重量10kg
抗力係数:Cd=0.04 および揚力係数:Cl=1.0 とした場合、
高度20kmの成層圏において風速30m/s 気体密度0.09(kg/m3)では、
揚力はL=1/2[0.09x30^2x20x1.0]=810 N( kg.m/s2)から、概略抗力と推力は
互いにキャンセルするので、自重分を差し引くと810N-(10kgx9.8m/s2)=712N
となる。
これは10kgの機体が70 (m/s2)の加速度(a)で風下に上昇する力である。
一秒後の移動距離は1/2(a・t^2)= 35mとなる。

滑空角はtanθ=Cd/Cl Cd=0.04 Cl=1.0の機体ではtanθ=0.04 なので
tan-1(0.04/1.0)=0.04 から θ=2.29と計算される。
滑空比Cl/Cd=25では、滑空しながら10m下降すれば横方向の移動距離は250mとなる。
また、滑空飛行においては、滑空速度Vは翼面積Sと翼面加重W/S(kg/m2)において
V=4√(W/S)x(1/√Cl)(m/s)である。
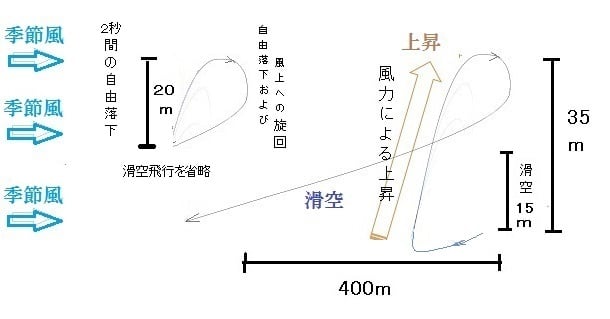
成層圏での相対風速30m/sにおいて、上記機体は約1秒で風下へ約35m上昇し、
自由落下2秒、20mの落下の後、相対速度を得て旋回飛行し、風上へ向かいながら
滑空下降で15mの下降、このとき風上への移動移動はおよそ400mの移動となる。
滞空時間サイクルは上昇が1秒、自由落下2秒、滑空が2.4分での滞空である。
翼面積20m2、総重量10kg では翼駆動機構や通信機搭載の実用機体では
相当にハードルが高い。サイクル滞空飛行については後日
また、総重量を増やすにはスケールメリットを活かすしかなく、飛行船と同様に
巨大化につながり、耐久構造部分においても重量との闘いとなる。
最近電動飛行機の開発が盛んに行われているため、当機体の駆動機構の
軽量化にも応用が可能であって、特に炭素繊維強化プラスチックは
高い強度と軽さを併せ持つ材料のため、航空機などの産業用に用途が
拡大しており安価・軽量・高耐久性に期待が持てる。
アサギマダラは渡りによって2,000kmもの距離を移動していることが知られている。
アサギマダラは昆虫であるが故、その渡りにおいては動力源が制限されている。
従って、上昇気流を使って上昇していると考えられている。
上昇の後には、滑空下降によって、下図のように風上への移動が可能となる。
その繰り返しで渡りを行う。


しかし上昇気流のない海をも渡ってくるので上昇気流だけでは説明が不十分だ。
そもそも10kmに一度の割合で上昇気流が無いと渡りができないとなれば、
秋の渡りにおいて、2、000kmもの距離を向かい風に向かって移動することは
不可能に近い。
ここで考えられるのは横風のみの風力エネルギーを利用した上昇飛行である。
滑空下降の途中で強い向かい風に遭遇したときに、翼の迎え角を大きく上げて、
揚力増大による上昇飛行を行うのである。何しろ揚力は相対気流速の二乗に比例して
増大するので、向かい風の強風は、上昇する時に大変効率的である。
従ってアサギマダラは翅面積の増大ではなく、強い風力エネルギーで高度を上げる
方法を選択し、翅を紙のように薄くし抗力を小さくすることで実現していると考えられる。
これが紙飛行機の様な蝶が動力もないのに、風力エネルギーによって2、000kmもの
距離を向かい風に向かって飛行する秘密である。

画面に向かって風が吹いている場合
アサギマダラの秋の渡りは上昇気流がなくても、風力エネルギーによっても上昇が
可能であることを教えている。
そうであれば成層圏のように、無尽蔵に風があり、尚且つ対流圏のような無風状態や
乱気流の無い空域での周回サイクル飛行が可能である。
一方滑空においては抗力を極力小さくすれば強風においても風上に進むことが可能で
加えて僅かな上昇移動であっても、風上への移動距離が長くなる。
そこでアサギマダラの渡りサイクルを短縮させれば、成層圏での滞空飛行が実現する。

上昇気流が無い場合の風上への移動飛行(秋の渡り)

下降によって風上の上昇位置に戻り、翼面積を広げて再上昇すれば滞空飛行となる。

尚、自由落下および風上に向かう旋回飛行の後、滑空は行わずに直ちに上昇すれば、
さらに短時間、狭い範囲での滞空サイクルの可能性さえある。(下図)


推力と重力の合成力(T+G)より、揚力と抗力(L+D)の合成の方が大きい場合に
上昇する。風上に向かう推力は自由落下の運動エネルギーによって得られる。
モデル機体での滞空飛行の可能性について
翼の軽量化をはかり、2枚の複葉として翼面積20m2、総重量10kg
抗力係数:Cd=0.04 および揚力係数:Cl=1.0 とした場合、
高度20kmの成層圏において風速30m/s 気体密度0.09(kg/m3)では、
揚力はL=1/2[0.09x30^2x20x1.0]=810 N( kg.m/s2)から、概略抗力と推力は
互いにキャンセルするので、自重分を差し引くと810N-(10kgx9.8m/s2)=712N
となる。
これは10kgの機体が70 (m/s2)の加速度(a)で風下に上昇する力である。
一秒後の移動距離は1/2(a・t^2)= 35mとなる。

滑空角はtanθ=Cd/Cl Cd=0.04 Cl=1.0の機体ではtanθ=0.04 なので
tan-1(0.04/1.0)=0.04 から θ=2.29と計算される。
滑空比Cl/Cd=25では、滑空しながら10m下降すれば横方向の移動距離は250mとなる。
また、滑空飛行においては、滑空速度Vは翼面積Sと翼面加重W/S(kg/m2)において
V=4√(W/S)x(1/√Cl)(m/s)である。
成層圏での相対風速30m/sにおいて、上記機体は約1秒で風下へ約35m上昇し、
自由落下2秒、20mの落下の後、相対速度を得て旋回飛行し、風上へ向かいながら
滑空下降で15mの下降、このとき風上への移動移動はおよそ400mの移動となる。
滞空時間サイクルは上昇が1秒、自由落下2秒、滑空が2.4分での滞空である。

翼面積20m2、総重量10kg では翼駆動機構や通信機搭載の実用機体では
相当にハードルが高い。サイクル滞空飛行については後日
また、総重量を増やすにはスケールメリットを活かすしかなく、飛行船と同様に
巨大化につながり、耐久構造部分においても重量との闘いとなる。
最近電動飛行機の開発が盛んに行われているため、当機体の駆動機構の
軽量化にも応用が可能であって、特に炭素繊維強化プラスチックは
高い強度と軽さを併せ持つ材料のため、航空機などの産業用に用途が
拡大しており安価・軽量・高耐久性に期待が持てる。















