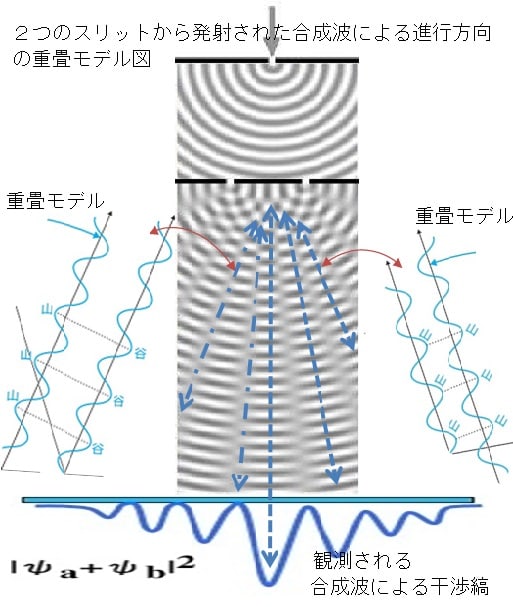
電子波は振幅と位相によって特徴付けられて表現される。且つ2つの波の合成によってはじめて観測される。
つまり干渉縞が現われることで、はじめて波であることが認識できる。従いその合成の表現法を知ることは
重要である。
複素空間(ガウス空間)において、2つの波の合成は次式であらわされる。
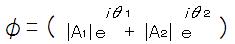
この時、波の観測強度/確率は共役複素数を掛けて以下の様に示される。
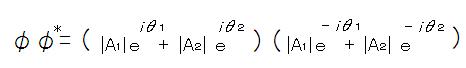
ここで波動の掛け算は指数のたし算で表示され、以下の例に示す通り

の計算を適応して、次式を得る

ここでオイラーの公式から

により
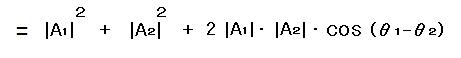
以上が合成された波の存在確率分布であり、この強度分布が観測される。
しかしいくら強い分布があってもその分布が均一であれば観測できない。
複素空間での波の合成計算後に、現実の実体強度に戻された合成波にも、
周波数と時間の要素が含まれ、時間軸で見れば位相項での周波数によって振動する。
電子顕微鏡では試料の構造に依存したCOS(θ1-θ2)の位相変調により、
その振動数による干渉縞が試料構造を反映した強度として観測される。
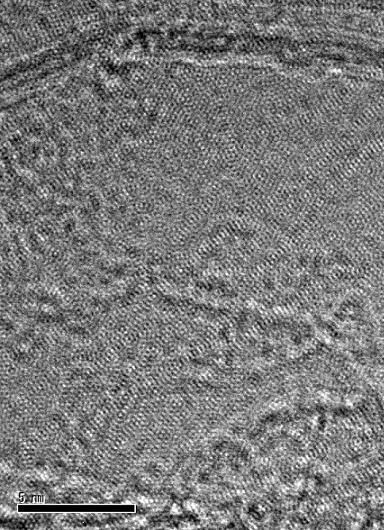
300kVの電子波とスリットとしてカーボングラファイトの面間隔(0.34nm)を
使用し、試料面より少しだけ遠い位置で合成波強度を見ると、COS(θ1-θ2)
の項に示す位相差による干渉によって小さな波紋が無数にでき、まるで湖面の
さざ波の様であった。これで確かに電子は波であることが見える化され実証された。
この時、波の振動を示す時間軸(右図)は写真の面に垂直の関係にある。