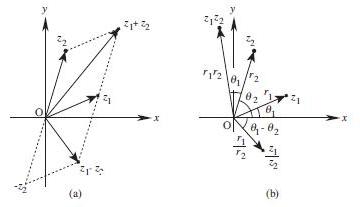
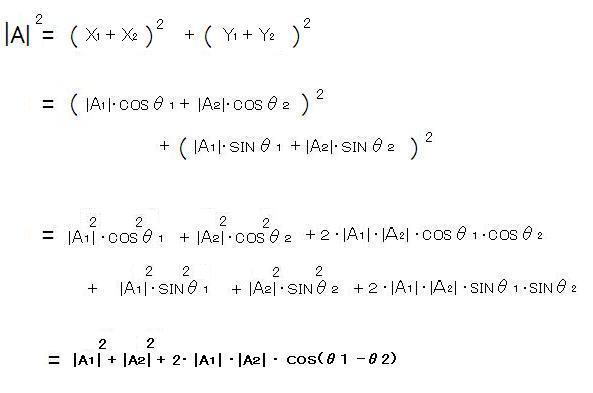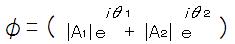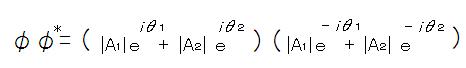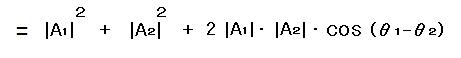極座標にて示されるベクトルZには、長さと方向に情報が含まれる。
波を表示する場合には、長さ|Z|が波の振幅(強さ)として、角度が
位相や周波数として表示さる。
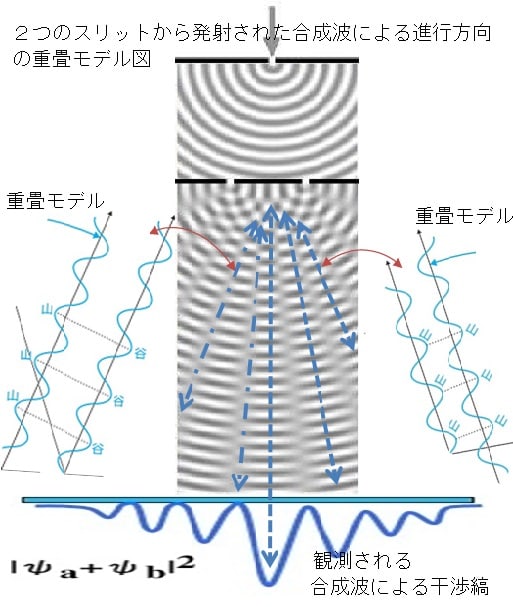
従ってベクトルの加減算|Z1±Z2|は合成(重畳)された波の振幅
として表現される。(a)
一方、ベクトルの掛け算では|Z1
・Z2|が長さで、角度(位相)は
反時計方向に加算されて回る。(b)
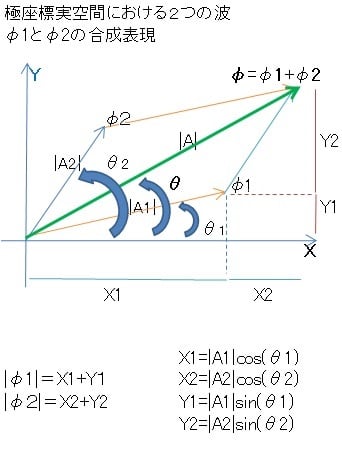
ベクトルによって表示される波φ1と波φ2によって合成された波φの
振幅強度が、
長さ|φ1+φ2|=|A|で示される。
その波が
観測強度/確率として観察される値は、合成波の二乗|φxφ|で示される。
それは二次元実空間で示す極座標ベクトルの長さ|A|の二乗であり、
即ち|φ1+φ2|の二乗である。この場合はX軸とY軸座標成分が混在してしまうので、
合成された波φの観測強度は
三平方定理によって、上図のX軸とY軸座標成分により求める。
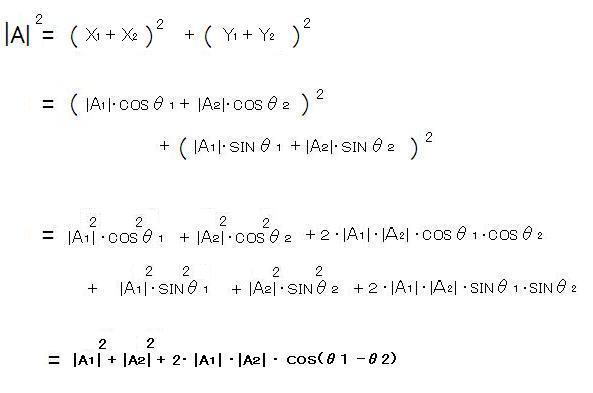
上記計算では次の定理を使う

一方、
複素平面(ガウス平面)を使えば同様に極座標表示において、合成された波は

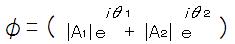
合成された波の
観測強度/確率は共役複素数を掛ければ求められるから、
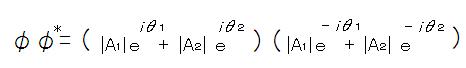
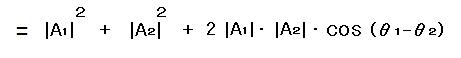
となって、合成波の
観測強度は、直行実平面と複素平面で共に一致する。
オイラーの公式によって複素平面では計算自体も非常にシンプルである。
オイラーの公式が指数関数と三角関数を虚数が媒介して成り立つ等式として「人類の至宝」や
「人類史に残る不朽の名作」と言われる所以である。
ここに改めてピタゴラスやオイラーの偉業を讃えるとともに、波の事例のみならずここで使われる
複素数の概念には、他の多くの複雑化した事象もシンプルに捉えられそうである。
シュレーディンガー70年の夢-波動関数の観測-2002-03-01永山 国昭著の最終章には、
「実数、実体、実在、虚数、虚構という日常的ことばが、認識に与えるバイアスに注意すべきで、
明確に言えることは複素数物理に慣れ、その実在感を獲得すると世界は極めて単純に表象かつ
理解できる。」とメッセージしている。
科学技術は万能ではなく、まして不確実なことを説明しようとすると大変な困難が伴う。
つまり誤解や不安を煽ったり風評被害が出たりすることがある。
従って科学技術には現実の姿をありのまま、解りやすく、正確にすることが必要不可欠であり、
リスク等が複雑なままでは必ず誤解が生ずる。だから正しいだけではだめで、具体的プロセスと、
それを正しく伝える手段がなければ使えないのと同じである。
それには複素数の概念が大いに役立ちそうだと私も常々感じている。
波の場合でも、SINとCOS、虚数と実数のように異質なものを成分ごとに分類して一体化させる
手法であったが、同じことが
料理をするときには、
食材とうま味成分を組み合わせるように、
家計簿では利益収入と、借入金を分別して記載するように、無意識でも既に実用化されている。
オイラーの公式COSθ+iSINθ=EXP(iθ)は
色+空=新たに目指す姿(新次元)という三位一体
としての関係が双方から見えてくる。
物事を「色」と「空」とに分けて混在させずに識別し、それが三位一体となった時、料理や家計簿の
例でいえば、料理を口に運び、あるいは収支決算での「実在感」が「色不異空」として獲得された時、
これが正に「シンプルにして見える化」であって、「世界は極めて単純に表象かつ理解できる」が
「色即是空」の部分だと思うのである。
付録:波の複素数表示
SINとCOSの2変数を使った複素数を用いる。波の特徴は進む速さ(位相)と強さであるが、
極座標表示における偏角の位相(Θ)部分で、波の波長と振動周期が使われる。