特殊相対性理論が示すような移動慣性系における物体の空間圧縮、つまりローレンツ収縮のイメージは真逆である。実際には、移動慣性系における物体は空間伸張するはずである。したがって高速移動物体の空間表現を、ローレンツ収縮とするのは誤りであり、ローレンツ伸張とするのが正しい。
特殊相対性理論では、移動慣性系において物体の時間遅延・空間圧縮・質量増大が発生するとしている。いわゆるローレンツ収縮は、このうちの進行方向に対する空間圧縮を指している。これについての数理的な説明は、ローレンツ収縮のカテゴリーに記載する。ここでは時刻の非同時性の矛盾収束に対して、ローレンツ収縮イメージが果した役割とその欠陥を呈示するに留める。
特殊相対性理論で説明される時刻の非同時性は、以下のイメージ図の形で示せる。
いずれの図も、次の要領で表現されている。
・ 系の中央位置に光源があり、そこから等距離に離れた両端に向かって光を発信する。
・ 発信された光の現在位置を矢印(←・→)で表し、図を時系列に並べて光の軌跡を示す。
・ 光源の位置を丸(○)で表す。ただし最初の光源の位置は両方向矢印(⇔)で表す。
・ 時刻単位の小数表記を避けるため、記載の速度の時刻単位を9とする。したがって9時刻で距離1を進むなら、その速度を1とする。
① 静止した慣性系における、中央発信した光の両端への同時到着
下記のイメージ図は、次の要領で作成し、移動慣性系の外から移動慣性系と光の軌跡を追跡したものである。これは②以後の説明の基本となるイメージ図になる。
・慣性系は静止している
・光は慣性系中心0の光源から速度3で、両端の6に向かって発信
※速度単位については、冒頭の表記要領を参照
上記の図は、静止系において中央発信した光の両端への同時到着を示す。
② 移動する慣性系における、中央発信した光の両端への非同時到着
上記の両端への同時到着のイメージ図に対し、移動慣性系での両端への非同時到着を示すために、下記に次の要領でイメージ図を作成し、移動慣性系の外から移動慣性系と光の軌跡を追跡する。
・慣性系は右方向に速度1で移動 上記の図は、移動慣性系において中央発信した光の両端への非同時到着を示す。しかしこの非同時到着は、静止系を含むいかなる慣性系においても、中央発信した光が両端に同時到着すべきという、光速に対する一般的要請に反する。この要請は、異なる慣性系において光速が同じだという観測事実から引き出されている。 移動慣性系における光の左端到着時刻は、静止系の左端到着時刻より早い。逆に右端到着時刻は、静止系の右端到着時刻より遅い。これは、慣性系の外から見た左右両方向の光速が同じであるにも関わらず、移動慣性系の中では、進行方向に向かう光と、進行と逆方向に向かう光の速度が実質的に同じではないのを示す。 ③ 移動する慣性系における、中央発信した光の両端への同時到着(ガリレオ変換版) 上記②のような非同時性と光速の偏差の困難を解消するためにローレンツ変換が考え出されるのだが、ローレンツ変換による同時性回復の説明に進む前に、ガリレオ変換した光速による同時性回復の説明を例示する。ガリレオ変換とは、物体速度に慣性系の移動速度を加算する形で、物体の相対速度を絶対速度に変換する方法である。もちろん慣性系の移動方向が物体の移動方向と逆向きなら、速度変換は加算ではなく、減算により行われる。もし光速がそのような形で慣性系の移動速度に影響を受けるなら、上記の非同時性の困難を解消できる。 上記の図は、ガリレオ変換により、移動慣性系において中央発信した光が、両端に同時到着するのを示す。なるほどガリレオ変換は、非同時性の困難を解消し、かつ慣性系の中における光速の偏差の困難も解消する。とはいえガリレオ変換には、次の問題点が残っている。
問題点)慣性系の外から見た光速の偏差 慣性系の中において光速が同じであるにも関わらず、移動慣性系の外から見て、進行方向に向かう光速と、進行と逆方向に向かう光速が同じではない。上記②と違い、そもそも光速を慣性系の影響下に置くガリレオ変換は、想定の段階で既に、異なる慣性系で光速が同じだという事実に反している。 ④ 空間圧縮した移動慣性系における、中央発信した光の両端への同時到着(空間圧縮版) ローレンツ変換による同時性回復の説明に進む前に、空間圧縮による同時性回復の説明を例示する。空間圧縮は、進行方向に向かう物体速度を実質的に増大させ、進行と逆方向に向かう物体速度を実質的に減少させ、ガリレオ変換と同等の効果を見込むものである。もし空間がこのような形で慣性系の移動速度に影響を受けるなら、前出の非同時性の困難を解消できる。 上記の図は、空間圧縮により、移動慣性系において中央発信した光が、両端に同時到着するのを示す。注目すべきは、慣性系は時刻0の段階ですでに、移動速度に対応した慣性系全体の空間組成が変換し、移動慣性系の全地点が元いた地点から左端4に向かってずれている点である。これは、光を慣性系の中央から発信するという前提が、最初から崩れているのを意味する。 静止系から見た移動慣性系における光の両端到着時刻は、静止系の両端到着時刻より早い。それは空間圧縮がもたらす当然の結末である。距離を2/3に縮めれば、到着までの時間も2/3になる。結果的に静止系の光速よりも、移動慣性系の光速の方が実質的に3/2倍速い。これは、異なる慣性系で光速が同一だという事実に反する。 問題2)慣性系移動開始時点の慣性系中心から進行方向側の各地点の進行方向からの後退 上記の図で見ると、上記イメージ図では、空間圧縮の結果、時刻0における移動慣性系の左側4を除く全地点が、元々自分のいた空間位置から左側4に向かって位置がずれている。このために慣性系の左側4から進行方向側の各地点は、時刻0時点で進行予定と逆方向に移動し、慣性系の右端6に至っては、最終的に進行方向に対する遅れを取り戻すのに、上記イメージ図の6段目の時刻30までかかる。また慣性系の左側4から進行と逆方向の各地点は、時刻0の段階ですでに進行方向に向かって移動している。 問題3)慣性系移動開始時点の慣性系内の光源の進行方向への前進 上記の図で見ると、時刻0における移動慣性系の圧縮が発生した際に、移動慣性系内で光源が進行方向に移動している。つまり光を慣性系の中央から発信するという前提が、最初から崩れている。このために2段目の時刻3までの間、光源から左端に向けて発信された光は、再度自らの発信地点0を乗り越えるべき位置にいる。 ⑤ 上記④の補正その1(空間圧縮+時間急進版) 上記④で示した空間圧縮の問題1、つまり慣性系の内外における光速の非同一は、移動慣性系内の空間圧縮にもとづく時間急進の発生により解消できる。もちろんローレンツ変換では、時間急進ではなく時間遅延により、移動慣性系内の光速と静止系の光速の同一化を狙うのだが、それは明らかな勘違いである。早くなった光の動きに対して、移動慣性系内の時間進行を遅くしても、移動慣性系内の物体運動は、ますます光に取り残されるだけである。 上記の図は、時間急進により、上記④で生み出された第一の困難を解消し、慣性系の内外における光速を同じにするのを示す。しかしここでも上記④で生み出された第二の困難と第三の困難、つまり慣性系移動開始時点の慣性系中心から進行方向側の各地点の進行方向からの後退と慣性系移動開始時点の慣性系内の光源の進行方向への前進という問題を解消できない。そしてさらに致命的な新しい困難に遭遇する。慣性系の内外における光速を同じにするために導入したはずの時間急進は、次のような問題点を生み出すためである。
問題点)光の高速化に対し、慣性系への時間急進の導入による対抗は不可 移動慣性系の時間急進は、高速移動する慣性系において時間遅延が発生する観測事実に反する。既に広く知られたこの観測事実は、なぜか相対性理論を実証する証拠とみなされている。 ⑥ 上記④の補正その2(空間圧縮+時間急進+分散型空間版) ここで一旦、慣性系の内外における光速の非同一、つまり上記④で示した空間圧縮の問題の一つ目をひとまず無視する。ここでは先に、慣性系移動開始時点の慣性系中心から進行方向側の各地点の進行方向からの後退、つまり空間圧縮の二つ目の問題の解消方法を説明する。この二つ目の問題は、移動慣性系内の空間圧縮を分散型空間圧縮に変えることにより解消できる。この分散型空間圧縮は、空間をライプニッツ型単子に扱うのを前提にしており、そのように空間を扱うことで上記の空間圧縮イメージを次のように変える。 分散型圧縮空間では、空間と空間の間に何も無い間隙が発生する。一方で光は空間の中だけを進行できる。このために、結合型圧縮空間よりも大きい分散型圧縮空間を進行する光速と、結合型圧縮空間を進行する光速を同じにするのが可能となる。つまり見た目の空間圧縮を必要とせずに、実質的な空間圧縮が可能となる。 上記の図は、分散型空間の導入により、空間圧縮後の移動慣性系内の各地点の同一性を保持している。つまり分散型空間は、上記④で生み出された第ニの困難を解消し、慣性系移動開始時点の慣性系内のほぼ全地点が進行予定位置に移動するのを可能にした。ただしここでは、上記④で生み出された第一の困難と第三の困難、つまり慣性系の内外における光速の非同一と慣性系移動開始時点の慣性系内の光源の進行方向への前進という問題を放置したままである。 ⑦ 記④の間違った補正その3(空間圧縮+時間遅延版、つまりローレンツ収縮版) 上記④⑤⑥の記述は、空間圧縮と時間遅延の導入、つまりローレンツ収縮が、上記④で示した空間圧縮の問題1、つまり慣性系の内外における光速の非同一を解消できずに、さらに困難を増幅することを示した。ここではそのローレンツ収縮の誤謬を明示するために、上記④の空間圧縮版のイメージ図に時間遅延を導入し、静止系と移動慣性系の時間進行を明示した下記の図を掲載する。 遅くなった時間進行は、移動慣性系の中での左右両端への到着を系内時刻8で達成させる。それは、静止系での左右両端への到着が時刻18だったのと比べると異常に早い。これは上記④での時間進行調整をしない場合の左右両端への到着時刻12よりも早い。圧縮空間での時間遅延は、移動慣性系の中の光速を加速させてしまうが、求められているのは光速の増大ではなく、減少である。 ⑧ 上記④の補正その4(空間伸張+時間遅延版) 上記までの記述で明らかなように、空間圧縮は時間遅延ではなく時間急進を要請するが、それは移動慣性系における時間遅延の発生という観測事実に反する。したがって要請されるべきなのは空間伸張となる。 上記のイメージ図では、先の④で登場した問題1、つまり慣性系の内外における光速の非同一は、移動慣性系内の空間伸張にもとづく時間遅延の発生により解消している。また同じく④の問題2、つまり慣性系移動開始時点の慣性系中心から進行方向側の各地点の進行方向からの後退も、空間伸張により解消している。しかし同じく④の問題3、つまり慣性系移動開始時点の慣性系内の光源の進行方向への前進は、まだ解消していない。
この問題3は、空間の圧縮伸張と無関係に発生しており、期待される実現結果から逆算する形で、時刻0時点の空間組成を変換したガリレオ変換の逆転を方法的に選択した時点で、すでに宿命づけられた困難である。 ⇒「時刻の非同時性(その2)」に続く
・光は慣性系中心0の光源から速度3で、両端の6に向かって発信
※速度単位については、冒頭の表記要領を参照
この図の抱える問題点は、以下のように纏まる。
問題点)慣性系の中における光速の偏差
このガリレオ変換による両端への同時到着を示すために、下記に次の要領でイメージ図を作成し、移動慣性系の外から移動慣性系と光の軌跡を追跡する。
・慣性系は右方向に速度1で移動
・光は慣性系中心0の光源から、両端の6に向かって発信
・もともと静止系で3だった光速は、進行方向に向かう光速では、慣性系の移動速度1が加算されて、光速4に加速。
・もともと静止系で3だった光速は、進行の逆方向に向かう光速では、慣性系の移動速度1が減算されて、2に減速。
※速度単位については、冒頭の表記要領を参照
結果的に下記のイメージ図は、慣性系の中から見た左右両方向の光速の同一性を保持した図となる。
この空間圧縮による両端への同時到着を示すために、下記に次の要領でイメージ図を作成し、移動慣性系の外から移動慣性系と光の軌跡を追跡する。なおここでは、空間圧縮率の数値的整合性に意味は無い。とにかく値が縮小さえすれば良く、それだけでここでの結論の正当性を示すことができるはずである。
・慣性系は右方向に速度1で移動
・光は慣性系中心0の光源から速度3で、両端の6に向かって発信
・移動慣性系に空間圧縮を導入
・慣性系は時刻0以前に既に移動継続中であり、空間圧縮の発生タイミングをそれ以前の過去と想定
・時刻0における移動慣性系の空間圧縮イメージを記載
・空間圧縮率は2/3
※速度単位については、冒頭の表記要領を参照
結果的に下記のイメージ図は、移動慣性系の外から見た左右両方向の光速の同一性を保持した図となる。
このことのほかに、ガリレオ変換と空間圧縮の各方法について、注目すべき差異を以下に纏めた。
・光の左右両端への最終的な同時到着の実現方法
ガリレオ変換:左右各方向の光の速度比の変更
空間圧縮 :左右各方向の距離比の変更
・実質的な光源位置
ガリレオ変換:最初の光源の位置
空間圧縮 :最終的な光の両端同時到着時の光源の位置
・左右両端の光源からの距離比変更の実現時刻と距離比
ガリレオ変換:最終的な光の両端同時到着時に1:2
空間圧縮 :最初の空間圧縮状態でに2:1
上記の注目点が示すのは、空間圧縮とは、その期待される実現結果から逆算する形で、時刻0時点の空間組成を変換しただけの、単なる逆転したガリレオ変換だということである。しかしこのようにガリレオ変換を逆転した空間圧縮は、非同時性の困難を解消し、かつ慣性系の内外における光速の偏差の困難も解消する。とはいえ空間圧縮は、新しく次のような問題点を生み出す。
問題1)慣性系の内外における光速の非同一
この時間急進による慣性系間の両端への同時到着時刻の整合を示すために、下記に次の要領でイメージ図を作成し、移動慣性系の外から移動慣性系と光の軌跡を追跡する。
・慣性系は右方向に速度1で移動
・光は慣性系中心0の光源から速度3で、両端の6に向かって発信
・移動慣性系に空間圧縮と時間急進を導入
・慣性系は時刻0以前に既に移動継続中であり、空間圧縮の発生タイミングをそれ以前の過去と想定
・時刻0における移動慣性系の空間圧縮イメージを記載
・空間圧縮率は2/3、時間急進率は3/2
・移動慣性系の外から見た左右両方向の光速の同一性を保持
・静止系と移動慣性系の時間進行を明示
※速度単位については、冒頭の表記要領を参照
結果的に下記のイメージ図は、時刻を明示した以外は基本的に④と同じになるが、慣性系間の両端への同時到着時刻が、静止系の時刻18と整合した図となる。
もし分散型圧縮空間を、分散した圧縮空間の外から見れるなら、分散した圧縮空間を通過する光の速度は、結合した圧縮空間を通過する光の速度よりも3/2倍速く見えるはずである。一方で空間の中にいる存在者にとって、そのような光速の増大を認知するのは不可能である。したがってこの分散型圧縮空間は、空間の中にいる存在者にとって、実質的に結合型圧縮空間と差異は無い。しかし先の、慣性系移動開始時点の慣性系中心から進行方向側の各地点の進行方向からの後退、という問題の解消には、この分散型圧縮空間は有意である。
この分散型空間による空間圧縮後の移動慣性系内の各地点の同一化を示すために、下記に次の要領でイメージ図を作成し、移動慣性系の外から移動慣性系と光の軌跡を追跡する。
・慣性系は右方向に速度1で移動
・光は慣性系中心0の光源から速度3で、両端の6に向かって発信
・分散型空間を導入
・移動慣性系に空間圧縮と時間急進を導入
・慣性系は時刻0以前に既に移動継続中であり、空間圧縮の発生タイミングをそれ以前の過去と想定
・時刻0における移動慣性系の空間圧縮イメージを記載
・空間圧縮率は2/3、時間急進率は3/2
・移動慣性系の外から見た左右両方向の光速の同一性を保持
・静止系と移動慣性系の時間進行を明示
※速度単位については、冒頭の表記要領を参照
ローレンツ収縮による慣性系間の両端への同時到着時刻の不整合を示すために、下記に次の要領でイメージ図を作成し、移動慣性系の外から移動慣性系と光の軌跡を追跡する。なおここでは、空間圧縮率と時間遅延率を同一に想定し、下記の移動慣性系の時刻表示を空間圧縮率2/3に合わせている。時間遅延率も、空間圧縮率と同様に数値的整合性に意味は無い。とにかく値が縮小さえすれば良く、それだけでここでの結論の正当性を示すことができるはずである。
・慣性系は右方向に速度1で移動
・光は慣性系中心0の光源から速度3で、両端の6に向かって発信
・移動慣性系に空間圧縮と時間遅延を導入
・慣性系は時刻0以前に既に移動継続中であり、空間圧縮の発生タイミングをそれ以前の過去と想定
・時刻0における移動慣性系の空間圧縮イメージを記載
・空間圧縮率は2/3、時間遅延率は2/3
・移動慣性系の外から見た左右両方向の光速の同一性を保持
・静止系と移動慣性系の時間進行を明示
※速度単位については、冒頭の表記要領を参照
結果的に下記のイメージ図は、時刻を明示した以外は基本的に④と同じになるが、慣性系間の両端への同時到着時刻が、静止系の時刻18と整合しない図となる。
④でも記述したが、そもそも空間圧縮は、期待される実現結果から逆算する形で、時刻0時点の空間組成を変換しただけの、単なる逆転したガリレオ変換である。したがって実現結果から逆算する形で、時刻0時点の空間組成を変換すれば良いのなら、別に空間圧縮である必要など元々無い。つまり空間伸張でも一向に構わなかったのである。
下記のイメージ図は、次の要領で作成し、移動慣性系の外から移動慣性系と光の軌跡を追跡したものである。
・移動慣性系は右方向に速度1で移動
・光は慣性系中心0の光源から速度3で、両端の6に向かって発信
・移動慣性系に空間伸張と時間遅延を導入
・慣性系は時刻0以前に既に移動継続中であり、空間伸張の発生タイミングをそれ以前の過去と想定
・時刻0における移動慣性系の空間伸張イメージを記載
・空間伸張率は3/2、時間遅延率は2/3
・移動慣性系の外から見た左右両方向の光速の同一性を保持
・静止系と移動慣性系の時間進行を明示
※速度単位については、冒頭の表記要領を参照
(2011/08/25)
※ 上記の空間伸張についての数理的説明は、ローレンツ収縮カテゴリーに記載している。
同カテゴリーの2011/02/27版を、図と数式を追加する形で、2011/08/28に改訂した。












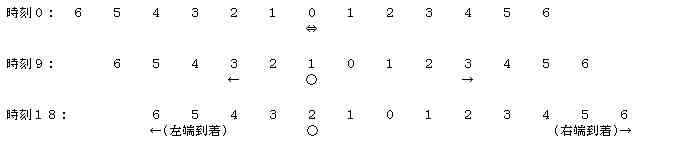











※コメント投稿者のブログIDはブログ作成者のみに通知されます