9)ヘーゲル弁証法における個の排除
労働力の大きさは、世代をまたがって存続すべき労働力を維持するための必要生活物資の総量として大きさを持つ。具体的にはなんらかの食材や衣料の各種総量であり、生活空間や家財の大きさであり、家族の養育に必要な各種資材の総量などの全体が、労働力の大きさを規定する。もちろんその大きさは、地域の歴史や文化、経済的成熟度を背景にして、ある程度の大きさの変化を許容する。要するにそれが表すのは、人に必要な生活資材の総量である。それに対して効用の大きさは、個々人の自由な恣意として現れる。例えばそれは、食事の満腹感や衣服への関心、居住空間に対する安心感や家族に対する愛情などの意識の漠然とした全体である。しかしその大きさは個々人において漠然としていながら、特定の瞬間において個々人の総体が得た効用の具体的な全体として実存する。それは社会全体が創出した富の全体である。すなわち、個々の商品が果たしてどれほどの効用の大きさを表すのか判らないとしても、その効用の全体は確固として意識の恣意から離れて現実に在る。それゆえにこの効用の全体を基準にして、個々の商品の効用を規定することは不可能ではない。ヘーゲルが量論の後段で論じるのは、質と量の相互転化の悪無限が、比例式の冪比例への進展において度量を生じる精神の運動である。直接的な質としての個物は、他者を媒介にし、その自己主張を表現する。しかしその他者もまた、別の他者を媒介にし、自らの直接的な質を表現せざるを得ない。その数理的表現は自己と他者の比であり、比例式である。ところがこのような質の規定に確固たる根拠は登場せず、比率はYをXで表現し、XをYで表現するだけの堂々巡りである。この悪無限の究極には、一方に不可知な物自体が現れ、他方に分解不能な原子が現れる。ヘーゲルがデモクリトス式原子論を馬鹿にするのも、原子に対し根拠としての非現実性を見出すからである。ヘーゲルにとって原子は、カント式物自体と同様に、根拠の要請に従い捏造された偶像にすぎない。この意味で労働価値論は、ヘーゲルからすればデモクリトス式原子論の経済学版であり、単なる価格原子論である。ヘーゲルにおいて精神の運動は、自己の全体を自己自身として超出し、脱自した自己は自己の外に自己自身を俯瞰する。すなわち自己は、自己否定を通じて自己自身を反省する理性となる。その自己に対して現れるのは、自己にとって過不足の無い全体である。その根拠としての確実性は、デカルト式コギトの確実性と同じである。ヘーゲルは単位としての原子から比例式を捉えるのを放棄し、総量としての全体から比例式を見直す。ここでヘーゲルが着目するのは、比例式Y=AXを構成する指数Aである。Aは原子Xが何かを問わずにYを規定し、翻ってXを規定する。Aが表現するのは、変動するXに対して固定したYの特性である。しかも同時にAはXの特性としてXに謬着する。すなわちAは、Yの本質を成すと同時にXの存在を構成する。それゆえにヘーゲルは比例式を逆比例式に転じ、指数AにおいてYを捉えることに専心する。これによりヘーゲルの関心はXから離れ、むしろ指数Aこそが根拠Xだと考えるようになる。
10)商品総量から現れる商品価値
商品総量から個別の商品価値を俯瞰する場合、実体は商品総量であり、個の商品はその単なる部分として現れる。商品総量に対する個の商品の比較は、両者の共通の要素を通じて行われるべきである。この共通要素の希求は、ヘーゲルの意に反し、商品の最小単位に原子を構成する。それゆえにここに労働価値論が登場する。商品総量は、商品生産にあたり投下された労働力の総体であり、個の商品はその単なる部分としての投下労働力の結晶だからである。一方で商品総量は、それが商品の塊である以上、使用価値の総体でもある。この場合に個の商品は、その単なる部分としての使用価値である。それゆえにここでもヘーゲルの意に反し、商品の最小単位が現れる。ただし限界効用理論が商品の最小単位として擁立するのは、この使用価値の質的差異を抽象化した効用である。ただし労働力に比べると効用は、商品総量の実体性を基準にするように見える分だけ、ヘーゲルの意に沿う。労働価値論の場合、商品の価値総量は商品一単位の生産に要する労働力に商品総量を乗じた値である。効用理論の場合でも商品一単位あたりの効用をもって、労働価値論と同様の仕方で価値総量を言い表わせる。しかし効用理論は、希少な商品に対する価格高騰と余剰な商品に対する価格微増を想定する。明らかにその価格想定は、固定と見られる価格総量を商品量で除した商品単価を元にしている。ただしその固定と見られる価格総量は需要商品総量であり、除数の商品量は供給商品総量である。したがってその想定単価は、供給商品一単位あたりの需要商品量で表わせる。もちろんその需要商品量が表すのは、供給商品一単位あたりの効用の大きさである。さしあたりこの材料で商品量に対応した効用曲線を描くことは可能となる。とは言え、需要商品量が表す効用の大きさはやはり不明瞭である。その不明瞭さは、需要商品量の代わりに効用の大きさに言い換えても変わらない。この点では労働価値論における労働力の方が明確である。それは人間生活に必要な生活資材の塊だからである。むしろ限界効用理論は、効用の大きさを明示的なものにしようとするなら、需要商品量を労働価値論式に需要者の生活と言い表した方が良い。あるいはもっと効用らしく言い換えるなら、効用を需要者の人生や生活と言い表した方が良い。そうすれば供給商品一単位当たりの効用は、人間の人生の4人分とか、人間の血肉の50人分と言い表わすことができる。例えば需要商品総量が100人分の生活に等しく、供給商品総量が20単位なら、その一単位当たりの効用は5人分の生活に該当する。このように現れた商品価値は、もちろん投下労働力量と一致しない。効用を労働力量で表現するのは、効用理論にとって不本意かもしれない。しかしこの説明では効用量の持つ不明瞭は払拭され、効用は俄然はっきりした姿で現れる。それゆえに限界効用理論における効用量の不明瞭に悩む効用論者は、この説明に喜ぶべきである。そして効用論者は、この説明に対して疑問を持つべきである。なぜならこの俄然はっきりした姿で見えてくる効用の姿は、支配労働価値説が説く代行労働力にすぎないからである。支配労働価値説にまつわる各種問題は先に示した通りである。効用論者はその全てを背負う必要がある。
11)供給商品総量と需要商品総量のずれ
効用の大きさは、供給商品総量を基準にして擁立されたものではなく、需要商品総量を基準にして擁立される。しかしその需要商品総量は、供給商品総量に根拠を持つ。このことは上記に示した効用量の明示例を使って示すことができる。上記例では供給商品一単位当たりの効用を5人分の生活として示した。しかしこの5人分の生活は、商品代価として購入者が供給者に支払う物資の大きさである。すなわちそれは商品購入者の欲望の上の現れる需要商品量ではなく、商品購入者が商品供給者に現実に供給する商品量、すなわち供給商品量である。商品購入者は商品効用を需要商品量に見立てる場合、自らが拠出する供給商品量において需要商品量が持つ効用の大きさを思い描く。また商品購入者はこの自らが拠出する供給商品量を元ネタにしなければ、欲望の上の現れる需要商品量がいかなる大きさを持つかを想像することもできない。そして次に商品購入者が思い描かねばならないのは、その供給商品量が持つ効用の大きさである。上記例の商品では、その効用の大きさは5人分の生活であった。具体的に言えばそれは、1人の人間が労働して生活資材を取得し、築き上げる人間生活の5倍である。ここまで分析を進めると不明瞭であった効用の大きさも、その大きさの基礎単位にいかなるものを据えているかも想定可能となる。要するに効用理論における効用の基礎単位は、やはり労働力なのである。もちろん上記想定は労働価値論式に立てた想定なので、それが労働価値論と類似するのは当然である。とは言え、いずれにせよ効用の基礎単位には何らかの人間生活の重みづけが必要であるのは、確かである。一方でこのことで露わになるのは、労働力が需要商品総量ではなく、供給商品総量を基準にしていることである。ここには一つの矛盾がある。総量に含まれるどの商品も、交換を考えない限りで単なる使用価値である。しかしそれが商品であり得るのは、使用価値に対する総需要の範囲内である。生産商品総量が、需要商品総量を超えるなら、その余剰部分は使用価値を失い、商品たり得ない。そのように供給商品総量における余剰部分の使用価値が失われるなら、供給商品総量と需要商品総量は使用価値において等価である。ところが供給商品総量における必要部分と余剰部分に現れる商品に差異が無いなら、商品がどちらの部分に属していても使用価値において等価である。したがって供給商品総量と需要商品総量は使用価値において等価ではない。この一方での等価が他方で不等価となる矛盾は、一見すると価値総量の確定と商品の単位あたり価値量の確定の間で起きる至極一般的な矛盾である。さしあたり判るのは、供給商品総量の減量、または需要商品総量の増量によりこの矛盾の解消が可能なことである。ただし供給商品総量の減量では需要商品総量が規定的に現れ、需要商品総量の増量では供給商品総量が規定的に現れる点に差異を持つ。そこで問題は規定的優位を供給と需要のどちらにたてるかに移る。需要に規定的優位をたてる場合、矛盾の解消は供給商品総量の減量を要求する。それは供給商品総量における余剰部分を商品総量の全体から締め出す要求である。しかしそこに含まれた個が全体から排除されると、排除された個に対応する需要も減量する。この悪無限は、供給商品総量の消滅まで連続しなければならない。ただしそもそも実存する個の排除は、矛盾の解消方向として現実的ではない。この現実性は、余剰商品部分を代表する個の商品供給者の生きる現実に根拠を持つ。それゆえに規定的優位はおのずと供給の側に移らざるを得ないように見える。しかしこの場合でも、規定的優位を需要の側にたてた場合の問題が逆方向で再現する。もともと余剰な供給商品部分に対応する需要は存在しない。それゆえに需要商品総量の増量が目指すのは、存在しない需要を創出し、それにより余剰な供給商品部分を商品総量の全体に復帰させる試みである。これが意味するのは、もちろんケインズ的施策を含めた社会主義的施策の試みである。そしてこの試みはことごとく失敗してきた。したがって矛盾の解消は、いずれにおいても困難に遭遇する。さてここには注目すべき一つの謎がある。それは供給商品総量と需要商品総量がもともと不一致であることの謎である。言い換えればそれは、総計一致命題の不成立の謎である。この話題は少し論旨とずれるので、以下に別枠としてまとめる。
11a)総計一致命題の不成立をめぐる共産主義の迷走
総計一致命題が求めるのは、総価値=総価格、かつ総剰余価値=総利潤である。この等式が成立するためには、商品における労働者の生活必要部分と労働者の生活不要部分を含めて全商品が市場で売れて、生活不要部分が利潤として不労資産家の元に還流しなければいけない。これについて剰余価値理論の急所としてバヴェルク以来指摘されてきたのは、商品価値の剰余部分、すなわち労働者の生活に不要な商品の存在が商品全体の需給バランスを最初から壊しているように見えることである。もともとこのことに対する共産主義の回答は、商品価値の剰余部分を不労資産家の需要として説明するものであった。しかしこの説明は、商品全体において成立するだけのガサツなものに見える。すなわちこの説明が成立するのは、或る商品が要求する余剰部分が、他方の商品の必要部分を食いつぶす場合だけに見える。実際には必要以上に特定商品を供給しても、不必要な特定商品はやはり売れない。例えば必要以上にハンマーを供給しても、不必要なハンマーはやはり売れない。不労資産家が剰余部分の大量のハンマーを自らの食事や衣服として使えるなら話は違うが、そのようなことはおよそ資産家が人間である限り不可能である。言い方を変えればそれは、剰余価値が利潤に転形出来ないのを表わす。もちろん市場において生活に必要な商品だけが売れるのであれば、今度は不労資産家のための利潤も生まれることができない。レーニンの帝国主義論はこの問題解決の一つの方向として成立するかもしれない。しかしそれは、一時しのぎの問題解決である。植民地経済が本国経済と一体化すると、植民地において不必要とみなされた個の商品が本国に参入し、需給バランスの不均衡がより激化して再燃する。そもそもマルクスは、資本論第一巻で産業予備軍なる無内容な概念を開陳している。そしてこの無内容な概念が示すのは、マルクス自身における総計一致命題の不成立についての自覚である。需要に対する供給の余剰部分は、そのまま給料未払いのまま放逐された失業者として現れる。この集積が産業予備軍だからである。しかしこの産業予備軍は生身の人間であり、恒常的に失業を続けるわけにいかない。もしその失業が持続するなら、この不必要とみなされた個の商品は、時間をおいてもれなく餓死する。なるほどこれらの個の商品の死滅を通じて需給バランスは回復し、総計一致を果たすかもしれない。しかしこのような矛盾の解消方向は、上記に筆者が述べたように現実的ではない。さらにこの総計一致は剰余価値理論に別の困難を持ち込む。すぐ判るようにこの総計一致は、商品価値の剰余部分の死滅に等しい。なぜなら産業予備軍の死滅は、そのまま剰余価値の捻出元の消滅だからである。それでも資本主義が剰余価値の取得を目指そうとすれば、資本主義は次々に産業予備軍を生み出し、その経済規模を縮小しながら貧民革命の勃発を自ら準備することになる。しかしこのようなことは資本主義の持続の上で合理的ではない。また実際にそのようなことは起きなかった。このような理論的問題を前にして露呈してくるのは、マルクスが投下労働力量と別に生産価格を擁立したのが、資本主義の持続を説明するための単なる理論的回避策にしか見えない現実である。ただしこのような理論的不利な状況であっても、剰余価値理論はたじろぐ必要はない。利潤発生の説明は、剰余価値理論においてのみ可能だからである。ここで注意すべきなのは、必要と需要、剰余と不要の言葉の混同である。
11b)総計一致命題不成立の眩惑
個々の商品生産で見たときにその供給商品の内訳は、労賃を含む原価相当の必要商品部分、資本家的利潤相当の剰余商品部分に分かれる。資本家的商品生産の目論見として言えば、供給商品量の目標量は、必要商品部分に加えて平均利潤相当の剰余商品部分の全体である。そしてそれらを完売すれば、この商品部門の企業家の資本家的満足と労働者の生活は充足する。この完売の条件は、供給商品量が需要商品量以下であり、需要商品量を超えないことである。もちろんこの条件の成立は、総計一致命題の成立に等しい。一見するとこの状態が、個々の商品に限らず全商品で展開されるなら、総計一致命題の不成立は起きない。しかし同じことを商品全体でみると、その必要商品部分はそのまま需要商品量として現れ、剰余商品部分はそのまま不要商品量として現れる。不要商品量は需要者に購入されず、購入されなければそれは利潤に転化できない。そのように剰余価値が利潤として現れないなら、やはり総計一致命題が成立しない。このチグハグは、個別に見た必要商品量の総体をそのまま商品全体で見た需要商品量に当て込み、剰余商品量の総体を不要商品量に当て込んだことから生じる。個別に見た需要商品量の総体は、必要商品量の総体ではないし、もともと供給商品量の総体である。したがって商品全体で見た供給商品量は、そのまま商品全体で見た需要商品量である。当然ながらその剰余商品部分は不要商品量ではない。そもそも個別で見ても不要商品量は登場しない。当然ながら剰余商品量は利潤に転化し、剰余価値は利潤と等しくなるし、総計一致命題も成立する。ここで浮かぶであろう疑問は、商品全体で見た剰余商品量が、なぜ需要から外れた不要商品量として現れるかである。もちろんこのことが言い表すのは、上記に示した総計一致命題の不成立の謎である。単純に言えばその不要性は、資本家的利潤の不要性に従う。逆に言えばそれは、資本家的利潤の必要性に応じて、やはり必要なのである。結果的に話は巡り巡って、バヴェルクへの回答は、共産主義の最初のガサツな回答に舞い戻る。すなわち商品価値の剰余部分を補填するのは、不労資産家の需要なのである。この場合にガサツな回答に対して要求すべきなのは、個別の商品部門における実現利潤の不均衡が、一方で剰余価値を食いつぶし、他方で過剰な剰余価値を生み出しながら、全体として均衡したときに平均利潤をもたらす経済運動の詳細な説明である。これは具体的に言えば、上記に例示した不要なハンマーの大量生産が需要量の範囲内に収束し、かつ平均利潤を実現する経済運動の詳細な説明を指す。ただしこの説明は表面的な解析技術を超えない話題である。もともとバヴェルクが問題にしたのは、このような表面的話題ではなく、総計不一致の原理的部分である。しかし総計不一致が資本家的利潤の不要性に従うのであれば、問題は最初から起きていない。そして平均利潤を実現する経済運動の説明が、さらにこの説明を補完する。すなわちバヴェルクへの回答は、上記の説明で十分に果たされている。商品価値論における転形問題の混乱は、マルクスとエンゲルスが二人三脚で引き起こした生産価格論と言う理論的不備に、バヴェルクが突っ込みを入れたことで引き起こされた。さしあたりバヴェルクに対して評価されて良いのはそこまでである。そこから彼が剰余価値理論と労働価値論の否定を結論付けたのは、非難に値すべき独断である。また生産価格論は、その価格と投下労働力量が一致しない点を否定的に捉えなければ、それなりに評価すべき点も多い。なぜならそれは、全体としての剰余価値の均衡と平均利潤の実現を説明するのにきわめて有効な議論だからである。この点で言えば、エンゲルスが述べたように、バヴェルクへの回答はやはり生産価格論だったことになる。見方によれば、産業予備軍の誤概念を提示したマルクス以上に、エンゲルスの方が正しく問題内容を把握し、その答え方を心得ていたのかもしれない。この点で見ても、バヴェルクに対する評価はさらに目減りする。ちなみに上記のチグハグと同じ形式で利潤の源泉を剰余価値以外から導出することができる。もちろんその言い表わすことは、永久機関が可能だとの歴史的発見である。このような発見に喜ぶ脳天気な輩には、おめでとうと言ってあげよう。
12)限界効用理論の一般的講評
総計一致命題の不一致は、供給商品総量と需要商品総量のずれによって引き起こされる。そしてこの供給商品総量と需要商品総量のずれは、資本家的利潤が需要を補わないことで発生する。簡単に言えばそれは、資本家的利潤の死蔵から発生する。これが無ければ、供給商品総量と需要商品総量は一致する。そしてこの一致は、商品の最小単位が固定の労働力であるのか、需給除算結果としての効用であるのかの価値定義の対立を終焉させる。むしろそれは、質料を持たず比率にすぎない効用概念の無内容を露呈させる。この場合に希少商品の価格高騰は、希少性にもとづく取得必要費用の増大を動機にして発生するだけであり、余剰商品の価格下落も、不要商品の在庫管理費用の減量を動機にして発生するだけである。いずれの費用もそのまま労働力に置き換えれば、ただの労働価値論である。このときに需給曲線を効用曲線に置き換えようとする限界効用理論の意義は、需給均衡図で説明されなかった需給均衡量以外の商品量の価格説明に収斂する。しかしこの試みは、需給曲線の消失において次の問題を生む。それは、効用曲線における価格高騰が価格下落に反転する動機の不在であり、価格下落が価格高騰に反転する動機の不在である。需給均衡図の場合、それぞれの反転の説明は、対抗する需給曲線の存在が説明してきた。しかし効用曲線はそれらを統合したために、その反転理由も同時に消失するからである。ただし効用理論にひいき目に見るなら、それらの動機も効用曲線の中に織り込み済みだと考えるべきであろう。効用曲線では商品量増加に伴って価格高騰が鈍化するが、供給曲線と同様に価格下落することは無い。このために高騰した価格の下落への道は商品量減少に託され、下落した価格の高騰への道も商品量増大に託される。しかし商品量減少が価格下落をもたらし、商品量増大が価格高騰をもたらすと期待する場合、その商品量は相対的な需給量でないと辻褄は合わない。すなわち需要減に対する供給増、または供給増に対する需要減が価格下落をもたらし、需要増に対する供給減、または供給減に対する需要増が価格高騰をもたらすべきである。この点では需給曲線以上に効用曲線は、商品量に対する価格の現れ方が硬直的である。もともと効用曲線は、需要曲線と同様の右肩下がりの価格曲線を描くわけではなく、供給曲線と同様の右肩上がりの価格曲線である。それゆえに効用曲線は、需要曲線における希少商品量での価格の極大値をいきなり発現できず、その代わりにロケットスタートで価格高騰のカーブを描く。同様に効用曲線は、需要曲線における余剰商品量での価格の暴落を描くことができず、その代わりに価格が下落しない水準で微増するようになる。希少商品量におけるロケットスタート、および上限価格の漸近線に並ぶ効用曲線の動きは、それぞれ希少時に極大値で始まり、商品余剰で暴落する需要曲線を供給曲線に取り込む無理から描かれる。しかし希少時に需要量が少なければ価格のロケットスタートは起きない。また商品余剰でも価格の原価割れを避けようとするなら、価格は上限価格の漸近線に並ぶことは無く、供給曲線に同化するはずである。これらの不自然は、効用曲線が座標の縦軸に商品総量に対する商品価格をとらず、縦軸に商品総量に対する商品単価をとっていることを予想させる。いずれにせよこのような需給曲線の統合の仕方は、単なる価格記録のグラフ化と同じであり、過去の価格運動の追認を超えない。すなわちそれは、わざわざ需要と供給に分離した需給均衡図の目論見を後退させたものである。したがってこのような価格曲線の硬直化は、やはり需給曲線からの後退である。そしてこのような退歩を進歩と勘違いする経済学的直観主義こそが、限界効用理論の本性になっている。
13)効用曲線
効用は、商品交換に関与することなく生まれる商品価値の度量であり、かつその度量で表わされる商品価値の大きさである。ただしその内実は、抽象化されることで一元的な大きさを得ただけの使用価値である。限界効用理論が想定する商品量に対応する効用曲線は、下記のように横軸に商品量,縦軸に効用量の座標に、或る最大効用量を漸近線にした反比例曲線の如く示される。ちなみに右の図は、比較のために例示した需給均衡図での需要曲線と供給曲線である。

効用曲線は、或る最大効用量を漸近線にした反比例曲線の如く現れる。ただしこの曲線は反比例曲線だとしてもその曲線に現れる効用量は、単純に最大効用量を商品量で割った値ではない。その反比例曲線は座標の漸近線の上側に現れるのでなく、下側に現れる上下逆さの反比例式だからである。その曲線での効用量は、商品量が少ないときに最大効用量より小さく、商品量が多いときに最大効用量の間近に達する。ちなみにこの縦軸の効用量は、商品一単位当たりの効用量なのか、横軸の商品量全部の効用量を指すのかは曖昧である。とりあえずここではまず縦軸の効用量を、横軸の商品量全部の総効用量と理解しておく。効用曲線の座標の縦軸目盛りを総効用量で捉えた場合、効用曲線は需給均衡図と同じ土俵で現れる。この場合だと効用曲線は、需要曲線と供給曲線を一体化した需給統一曲線として理解される。しかし効用曲線は、商品量が少ないときに効用量が小さく供給曲線寄りなので、希少な商品において高価格な需要曲線と対立する。一方で効用曲線は、商品量が多いときに効用量がほぼ一定に近い微増である。このことはまた余剰な商品において高価格な供給曲線に対立する。労働価値論式理解から見ても、座標の縦軸目盛りに総効用量を据えたときに、商品量の増加に対して価格が微増に留まるような効用曲線は異常である。このように反比例曲線として理解されるような効用曲線は、ある程度の商品量を超えると、どれほど商品量が多くてもその効用量は最大効用量を超えない。このような逆さの反比例曲線として理解される効用曲線の式は、次のように表現される。
逆さ反比例モデル効用曲線式:Y=A- A-B ![]()
X ※A:最大効用量、B:商品量1における効用量、X:商品量、Y:効用量
この効用曲線の動きを効用街道を走るバイクライダーの走りで例えると次のようになる。バイクライダーは、商品効用が商品量の少ないときに半スロットルで走り、商品量の増加に伴いそのスロットルをほぼ全開に持ってゆき、それ以後は商品量の増加に関わらずスロットル全開で走る。この一見するともっともらしい効用量の増加の仕方は、一方で希少な商品量の効用量について奇異である。それと言うのも、商品一単位あたりの効用量は、商品量の最初の一単位のときではなく、商品量が或る程度増大したときに、その最大値を示すからである。この奇異に対してどうしても出てくるのは、座標の取り方がやはり縦軸に商品一単位当たりの効用量なのかとの疑問である。そこでこの確認のために今度は、先の曲線式を単位当たり効用量版だとみなし、それを総効用量版に変換し、その効用曲線の現れ方を確認してみる。先の曲線式を単位当たり効用量と理解した場合、先の曲線式の右辺は商品量Xに対応する単位当たり効用量の式である。したがってこの式の右辺にさらに商品量Xを乗じると、今度は次のような商品量Xに対応する総効用量の式が得られる。
変換版逆さ反比例モデル効用曲線式:Ya=(A- A-B ![]()
X )X ※A:最大効用量、B:商品量1における効用量、X:商品量、Y:効用量
=AX-(A-B)
この変換版の効用曲線を表示する座標は、横軸に商品量、縦軸目盛りに総効用量をとったものとなる。総効用量をその商品量の商品価格と理解するなら、この座標は需給均衡図と同じ土俵で現れる。この変換した効用曲線の式と座標は、次のように表現される。

上記の変換効用曲線は、すぐ判るように需給均衡図の供給曲線と同じである。しかしそもそも効用理論が期待するのは、希少な商品における効用の逓増と余剰な商品における効用の逓減である。その目論むところは、或る一定の商品量における限界効用の出現である。もちろんその最大効用量が表すのは市場価格であり、それに対応する商品量は需給均衡量だと想定される。ところが先の効用曲線の座標の縦軸を商品一単位当たりの効用量で扱うと、そのような一定の商品量における効用の逓減を見込めない。したがって先の効用曲線の座標は、やはり縦軸に総効用量を据えるべきだと考えられそうである。ところがその一方で希少な商品における大きな効用と余剰な商品における小さな効用を縦軸目盛りが総効用量の座標で表わすと、単なる需要曲線が仕上がるだけである。それゆえに限界効用理論が期待する効用曲線は、やはり上記の図柄ではなく、下記の左図のような縦軸目盛りに単位当たり効用量を据えたものと考えられる。ちなみに右図は、上記の逆さ反比例モデルの効用曲線を市場単価版に変換したものである。この市場単価版の逆さ反比例モデルの効用曲線は、確かに希少な商品における効用の逓増と余剰な商品における効用の逓減を現す。しかしこの効用曲線での効用の逓増と逓減は、商品量が2個の時点で最大効用量が常に現れる。商品量が2個で最大効用量が現れる効用曲線は、商品量が1個の座標点を無視して言えば、単なる逓減曲線でしかない。そのような効用曲線は、やはり効用理論の期待に応えるものだと考えらえない。それゆえに以下ではこの市場単価版の逆さ反比例モデルの効用曲線を無視し、左図の効用曲線モデルを想定して効用曲線の現実性を確認する。
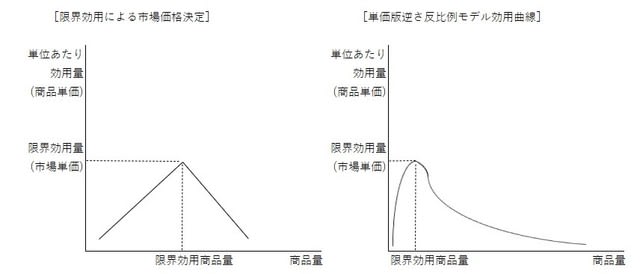
なお上記左の曲線図と需給均衡図は、座標縦軸の目盛りが相互に異なるので単純比較できない。しかし効用曲線図の縦軸目盛が単価の曲線式でも、上述容量と同様にその曲線式に商品量を乗じるなら、需給曲線図の座標と同じ縦軸単位で効用曲線を描ける。そこで次にそのような効用曲線図を作成して、それと需給曲線図と比較する。ただし限界効用理論が限界効用を、逓増する限界効用の逓減に向かう直前の効用上限として描く理由は、もともと不明瞭である。それゆえに縦軸単位を一致させた両図の比較の前に、縦軸に単位あたりの効用をとった効用曲線の効用量の逓増部分と逓減部分が、それぞれいかなる意味付けを与えられているかを確認する。
(2020/02/24) 続く⇒((4)需給曲線と限界効用曲線 前の記事⇒((2)使用価値の大きさとしての効用)
ヘーゲル大論理学 存在論 解題
1.抜け殻となった存在
2.弁証法と商品価値論
(1)直観主義の商品価値論
(2)使用価値の大きさとしての効用
(3)効用理論の一般的講評
(4)需給曲線と限界効用曲線
(5)価格主導の市場価格決定
(6)需給量主導の市場価格決定
(7)限界効用逓減法則
(8)限界効用の眩惑
ヘーゲル大論理学 存在論 要約 ・・・ 存在論の論理展開全体
緒論 ・・・ 始元存在
1編 質 1章 ・・・ 存在
2章 ・・・ 限定存在
3章 ・・・ 無限定存在
2編 量 1章・2章A/B・・・ 限定量・数・単位・外延量・内包量・目盛り
2章C ・・・ 量的無限定性
2章Ca ・・・ 注釈:微分法の成立1
2章Cb(1) ・・・ 注釈:微分法の成立2a
2章Cb(2) ・・・ 注釈:微分法の成立2b
2章Cc ・・・ 注釈:微分法の成立3
3章 ・・・ 量的比例
3編 度量 1章 ・・・ 比率的量
2章 ・・・ 現実的度量
3章 ・・・ 本質の生成















※コメント投稿者のブログIDはブログ作成者のみに通知されます