関数は何故難しいと思うの？どこが難しいの？ （シリーズ２）

　関数では、比例・反比例　　a＝決まった数   　ｘ軸　ｙ軸　交点　原点　絶対値　偶数・奇数　　曲線直線　式・表・グラフ　　ax   a/x    約数（因数）　方向　　領域　　図形　座標　　双曲線など色々な言葉が出てきますので理解できない生徒は、ほとほと困ります。

　関連付けが出来ないでいるのです。とりわけ重要なのは「座標」なのです。ｘ軸ｙ軸によって座標の位置という事を知るのですが、この座標を指導する際に４つのパターンを徹底して教える必要があります。

　（＋２・＋４）（＋３・－６）（－５・＋８）（－１２・－２）この４つなのですが、多くの生徒さんは、このような座標表示は得意としていますが、この先どのように使いこなすかが分かっていません。座標はご存じのように（xの値・ｙの値）というように一般通念上周知されています。これをもっと広く他の面に繋げるように指導する必要があります。

　例えば、上記の（＋２・＋４）は、絶対値に絡めて絶対値の大小の指導で終わらずに＋・＋の方向と２と４の絶対値の乗算によって、８と言うaが見つかりそれがｙ＝８/xという関係式が作られて８と言う約数によって反比例の曲線が作られる。

　そして次に領域設定で、その領域が＋になるものか？－になるものか？の判断ができるところまで教える事が必要です。この部分が中学校の大部分で今尚指導が抜け落ちているという大失態をやらかしているのです。いち早くどんな先生（担当科目が違ってもという意味）でもいいから気付いて欲しいのです。

 

　（＋・＋）の箇所を（＋）の領域と設定すれば、おのずと（－・＋）（＋・－）の箇所は（－）と設定できて、（－・－）の箇所は（＋）になるんだということを、そう難しくなく指導できるのです。

 

　座標のxyを掛けると、反比例の計算結果を示します。なぜならｙ＝a/xだからです。するとその領域が、＋領域であればｙ＝a/x  －領域であればｙ＝－a/xと一目瞭然関係式が分かるというものです。

　生徒さんたちにとって随分と役立つと思います。

　　　指導者の皆様、このあたりの研究を是非とも進めて頂きたいと思います。

　　　下手な文章はお許し下さい。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

関数学習の基本は、小学６年反比例・比例と中１符号問題です シリーズ（１）

　今までの投稿と重複する所、多々あるかも知れませんがご了承ください。

　出来るだけ簡単明瞭に、短編にてシリーズの形で投稿をして参りますので

理解が進んで他人に説明が出来るようであれば、お友達などにどしどしお伝え

下さい。およそ１２００文字までを１回分とします。

　　小学校では、比例式としてY=決まった数×　Ｘ　反比例式としてY=決まった数÷X

　　　　　　　　　と習いました。

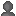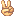　　中学校では、比例式がY=ａXとなり　反比例式がY=ａ／X（／は分数です）と

　　　　　　　　　習います。決まった数の事を（ａ）にしているに過ぎません。

そこで、ａ＝（決まった数）の求め方を一度確認しておきましょう。

　比例では、ａ＝Ｙ／X　　　反比例では、ａ＝ｘｙとなりますね　　　そこでこのｘｙは

すなわち、（－４・＋６）表記の座標であると考えるとつながりませんか？　さらにこの

座標（－４・＋６）を符号計算問題の　（－４）×（＋６）とつながりませんか？というのが

今回の投稿の考えていただく目的です。じっくりとお考え下さい。（中学生頑張って）