ネクサス(江南市の勉強のやり方専門塾)の塾長の伊藤です。
小学5年生で割合を習う季節になりました。
割合は速さと並んで算数でもっともつまずきやすい単元の一つとされています。
しかし、正しく文章を読む練習をすれば、それほど難しい単元ではないことがわかります。
「はじき」と並んで小学校でゾンビのように生き残っている公式に「くもわ」があります。
「くもわ」とは、
く=くらべる量
も=もとにする量
わ=割合
といった具合に、「はじき」をまねた公式です。

「はじき」ほどではないですが、割合で「くもわ」の公式を使っている子をときどき見かけます。
「はじき」は弊害も多いですが、その使い勝手の良さから学校では好んで使われているようです。
ところが、「くもわ」は弊害しかない最凶の公式といっても過言ではないでしょう。
全国学力テストから、次の問題を例に考えてみましょう。
■2008年「全国学力・学習状況調査」(文科省)
4.テープが3本あります。テープの長さは次のようになっています。
・赤色のテープの長さは3m
・青色のテープの長さは6m
・黄色のテープの長さは12m
(1)黄色のテープの長さは、赤色のテープの長さの何倍ですか。 正答率【83.1%】
(2)青色のテープの長さは、黄色のテープの長さの何倍ですか。 正答率【55.7%】
(1)の問題は「黄色は赤色の何倍か」を求めるので、黄色÷赤色、つまり12÷3=4倍と計算すれば求められます。
(2)の問題は「青色は黄色の何倍か」を求めるので、青色÷黄色、つまり6÷12=0.5倍と計算すれば求められるのですが、12÷6を計算している子が24.0%もいました。
また、クロス集計の結果、(1)と(2)の両方とも正答した子は52.5%しかおらず、多くの子がよく考えずに「大きい数÷小さい数」をやっているだけという実態がわかりました。
さて、この問題「くもわ」の公式を使って解ける子がいったいどれだけいるでしょうか。
そう、どれが「く=くらべる量」で、どれが「も=もとにする量」かわからないのです(笑)。
学校の先生によっては、「~は」と書いてあるのがくらべる量で、「~の」と書いてあるのがもとにする量と教えているようです。
確かに。
だったら、無理に「くもわ」の公式に落とし込まなくても解けますよね(笑)。
そもそも、「はじき」の公式のところでも取り上げましたが、割合や速さの問題が解けない原因は、数字だけを「つまみ読み」しているからです。
先ほどの(2)の問題では、多くの子が青色(=6m)と黄色(=12m)から6と12を計算に使えばよいということまでは読み取っていても、どちらがどちらの何倍かまでは読み取っていません。
かけ算では交換法則が成り立つため6×12も12×6もどちらで計算しても答えは一緒になります。しかし、わり算では交換法則は成り立ちません。
算数が苦手な子は、交換法則が使えないのにも関わらず、わる数とわられる数を勝手に入れ換えてしまうという思考の弱さがあります。
つまり、負荷のかかる6÷12より、簡単に答えが出せてしまう12÷6を好んで計算してしまう子が多いのです。
このような一種のギミックに子どもはまんまとひっかかってしまうわけですが、もっとも考えなければいけないのは問題文を読まずに数字をつまみ読みすることです。
次のような問題でその点を考えてみます。
■割合(百分率)の問題
ジュースを0.6L飲みました。飲んだ量ははじめにあったジュースの20%です。はじめにあったジュースは何Lですか。
この問題では、
はじめにあったジュースの20%が飲んだ量(飲んだ量ははじめにあったジュースの20%)
という関係性が読みとれることが何よりも重要です。
■わからないものを□と考えて関係性を読み取る
・はじめにあったジュースの量→□
・の20%→×0.2
・飲んだジュースの量→0.6L
はじめにあったジュースの20%が飲んだ量
↓
□×0.2=0.6
こうして、まず言葉の式で考えたものを、次はわからないものを□と考えて□を使った式で考えるようにします。
そうすることで□×0.2=0.6という式を立てることができ、3年生で習った□を使った式を応用することで、□=0.6÷0.2を計算すればよいということがわかります。
数字をつまみ読みするだけの子は、0.6と20という数字だけを使って「くもわ」の公式にあてはめて解くかもしれません。
もちろん、20%という数字が0.2(倍)ということがわかっても、どれが「く」でどれが「わ」かわかってないと解けないというおかしな現象が起こります。
確かにこの問題では百分率が一種のひっかけとなっていますが、「何が何の何倍か」という関係性を読み取ることさえできれば、0.6の20倍でないことはわかるはずです。
結局、「はじき」にしろ「くもわ」にしろ、問題文から数字をつまみ読みするだけで「何が何の何倍か」を読み取らない子にとっては、ますます問題文を読まずにつまみ読みを助長するという点では同じなのです。
子どもがつまずかない教師の教え方65のアイデア(東洋館出版社)

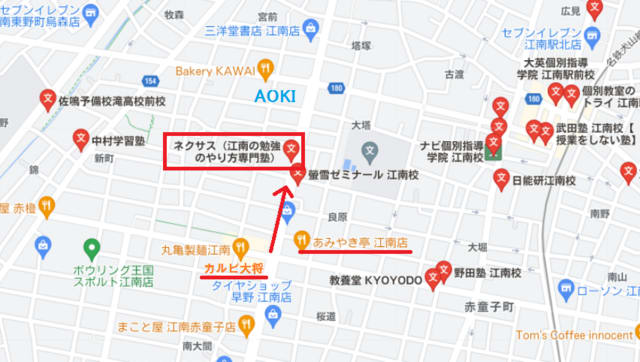
■教室はココ!(483-8226江南市赤童子町大間97-1柴垣事務所2F)
【入塾までの流れ】
1.お電話・LINEにてお申込み
↓
2.個別の説明会 ※通知表やテスト等をお持ち下さい
↓
3.体験授業(1~4回まで無料)
↓
4.正式入塾!
■LINE

■メールフォーム
生徒氏名(ふりがな)、学校名、学年、連絡先、お問い合わせ内容(個別の説明会/ご相談など)を明記して下さい
▼問い合わせをする(ここをクリック)▼
(※スマホから送信する場合は「転送~」をクリック、送信確認画面まで進んで下さい)
■TEL
090-4268-4939(12時~22時、伊藤まで)
ネクサスは、主に一宮高校、江南高校、一宮南高校、名古屋西高校、尾北高校、丹羽高校、岩倉総合高校の高校生と、そこを目指す小中学生が通っています。江南市では、古知野中学校、布袋中学校、江南西部中学校、宮田中学校、一宮市では千秋中学校、西成中学校、西成東部中学校、岩倉市では岩倉中学校、大口町では大口中学校の中学生が通っています。
■空席状況をチェック
・学年ごとの曜日・空席状況がチェックできます
小学5年生で割合を習う季節になりました。
割合は速さと並んで算数でもっともつまずきやすい単元の一つとされています。
しかし、正しく文章を読む練習をすれば、それほど難しい単元ではないことがわかります。
「はじき」と並んで小学校でゾンビのように生き残っている公式に「くもわ」があります。
「くもわ」とは、
く=くらべる量
も=もとにする量
わ=割合
といった具合に、「はじき」をまねた公式です。

「はじき」ほどではないですが、割合で「くもわ」の公式を使っている子をときどき見かけます。
「はじき」は弊害も多いですが、その使い勝手の良さから学校では好んで使われているようです。
ところが、「くもわ」は弊害しかない最凶の公式といっても過言ではないでしょう。
全国学力テストから、次の問題を例に考えてみましょう。
■2008年「全国学力・学習状況調査」(文科省)
4.テープが3本あります。テープの長さは次のようになっています。
・赤色のテープの長さは3m
・青色のテープの長さは6m
・黄色のテープの長さは12m
(1)黄色のテープの長さは、赤色のテープの長さの何倍ですか。 正答率【83.1%】
(2)青色のテープの長さは、黄色のテープの長さの何倍ですか。 正答率【55.7%】
(1)の問題は「黄色は赤色の何倍か」を求めるので、黄色÷赤色、つまり12÷3=4倍と計算すれば求められます。
(2)の問題は「青色は黄色の何倍か」を求めるので、青色÷黄色、つまり6÷12=0.5倍と計算すれば求められるのですが、12÷6を計算している子が24.0%もいました。
また、クロス集計の結果、(1)と(2)の両方とも正答した子は52.5%しかおらず、多くの子がよく考えずに「大きい数÷小さい数」をやっているだけという実態がわかりました。
さて、この問題「くもわ」の公式を使って解ける子がいったいどれだけいるでしょうか。
そう、どれが「く=くらべる量」で、どれが「も=もとにする量」かわからないのです(笑)。
学校の先生によっては、「~は」と書いてあるのがくらべる量で、「~の」と書いてあるのがもとにする量と教えているようです。
確かに。
だったら、無理に「くもわ」の公式に落とし込まなくても解けますよね(笑)。
そもそも、「はじき」の公式のところでも取り上げましたが、割合や速さの問題が解けない原因は、数字だけを「つまみ読み」しているからです。
先ほどの(2)の問題では、多くの子が青色(=6m)と黄色(=12m)から6と12を計算に使えばよいということまでは読み取っていても、どちらがどちらの何倍かまでは読み取っていません。
かけ算では交換法則が成り立つため6×12も12×6もどちらで計算しても答えは一緒になります。しかし、わり算では交換法則は成り立ちません。
算数が苦手な子は、交換法則が使えないのにも関わらず、わる数とわられる数を勝手に入れ換えてしまうという思考の弱さがあります。
つまり、負荷のかかる6÷12より、簡単に答えが出せてしまう12÷6を好んで計算してしまう子が多いのです。
このような一種のギミックに子どもはまんまとひっかかってしまうわけですが、もっとも考えなければいけないのは問題文を読まずに数字をつまみ読みすることです。
次のような問題でその点を考えてみます。
■割合(百分率)の問題
ジュースを0.6L飲みました。飲んだ量ははじめにあったジュースの20%です。はじめにあったジュースは何Lですか。
この問題では、
はじめにあったジュースの20%が飲んだ量(飲んだ量ははじめにあったジュースの20%)
という関係性が読みとれることが何よりも重要です。
■わからないものを□と考えて関係性を読み取る
・はじめにあったジュースの量→□
・の20%→×0.2
・飲んだジュースの量→0.6L
はじめにあったジュースの20%が飲んだ量
↓
□×0.2=0.6
こうして、まず言葉の式で考えたものを、次はわからないものを□と考えて□を使った式で考えるようにします。
そうすることで□×0.2=0.6という式を立てることができ、3年生で習った□を使った式を応用することで、□=0.6÷0.2を計算すればよいということがわかります。
数字をつまみ読みするだけの子は、0.6と20という数字だけを使って「くもわ」の公式にあてはめて解くかもしれません。
もちろん、20%という数字が0.2(倍)ということがわかっても、どれが「く」でどれが「わ」かわかってないと解けないというおかしな現象が起こります。
確かにこの問題では百分率が一種のひっかけとなっていますが、「何が何の何倍か」という関係性を読み取ることさえできれば、0.6の20倍でないことはわかるはずです。
結局、「はじき」にしろ「くもわ」にしろ、問題文から数字をつまみ読みするだけで「何が何の何倍か」を読み取らない子にとっては、ますます問題文を読まずにつまみ読みを助長するという点では同じなのです。
子どもがつまずかない教師の教え方65のアイデア(東洋館出版社)

■教室はココ!(483-8226江南市赤童子町大間97-1柴垣事務所2F)

【入塾までの流れ】
1.お電話・LINEにてお申込み
↓
2.個別の説明会 ※通知表やテスト等をお持ち下さい
↓
3.体験授業(1~4回まで無料)
↓
4.正式入塾!
■LINE

■メールフォーム
生徒氏名(ふりがな)、学校名、学年、連絡先、お問い合わせ内容(個別の説明会/ご相談など)を明記して下さい
▼問い合わせをする(ここをクリック)▼
(※スマホから送信する場合は「転送~」をクリック、送信確認画面まで進んで下さい)
■TEL
090-4268-4939(12時~22時、伊藤まで)
ネクサスは、主に一宮高校、江南高校、一宮南高校、名古屋西高校、尾北高校、丹羽高校、岩倉総合高校の高校生と、そこを目指す小中学生が通っています。江南市では、古知野中学校、布袋中学校、江南西部中学校、宮田中学校、一宮市では千秋中学校、西成中学校、西成東部中学校、岩倉市では岩倉中学校、大口町では大口中学校の中学生が通っています。
■空席状況をチェック
・学年ごとの曜日・空席状況がチェックできます