いまどこ ―冒頭表示2
キーボードの2段めと3段目はなぜ互い違いになっていないの - 教えて!goo:
に答えてってな形で部分統合しようかナとも思う。
http://blog.goo.ne.jp/raycy/e/c11db5b33d4a1d67900e568ab0dc6273ではちょっとスレ違うと思う。
http://www6.atpages.jp/~raycy/Q/ を http://www6.atpages.jp/raycy/blog2btron/door やらの作業経過を取り入れつつ、ふくらませるようなかんじで、、
http://www6.atpages.jp/~raycy/Q/ を http://www6.atpages.jp/raycy/blog2btron/door やらの作業経過を取り入れつつ、ふくらませるようなかんじで、、
1882年版QWERTY配列でのアルファベット26文字部を並べ替えて隣接タイプバーの連続打字機会頻度を推定する。
1882年版QWERTY配列でのアルファベット26文字部のランダムな並べ替え案を 隣接タイプバーの連続打字機会頻度で評価する。
1882年版QWERTY配列での英字26文字部の擬似乱数による代替配列案を 隣接タイプバーの連続打字機会頻度で評価する。
1882年版QWERTY配列の英字26文字部へ擬似乱数で代替配列案、隣接タイプバーの連続打字機会頻度で採点する
現シミュレーションの問題点、
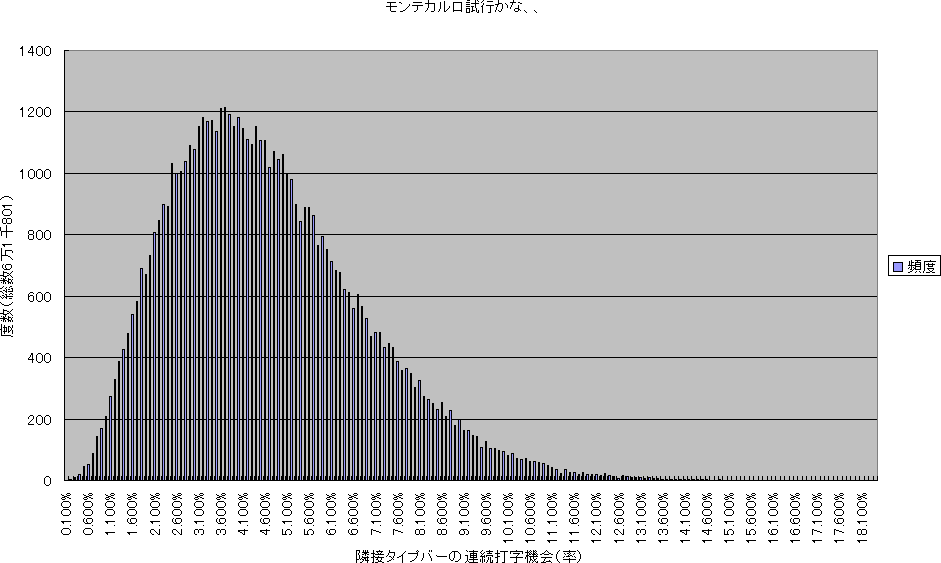
サンプル数――並べ替え代替オルタナティヴ提案数――が増えるほど、分布度数の荒さが減っていくようである。1万と6万では、6万提案のほうが、分布の乱れが減り、連続曲線状になっているようである。
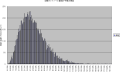

Y軸:順列度数-X軸:頻度区間,

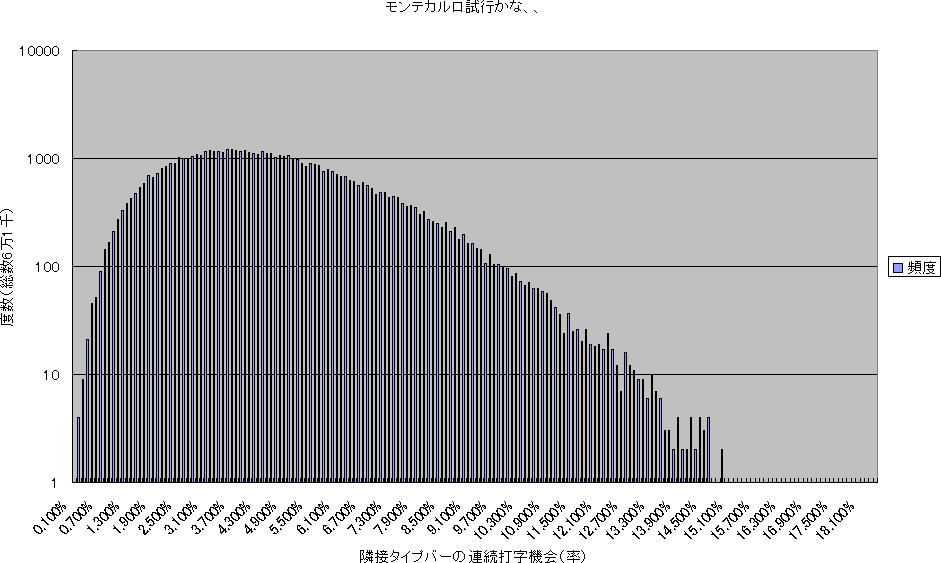
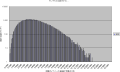 Y軸:対数順列度数-X軸:頻度区間,
Y軸:対数順列度数-X軸:頻度区間,
Y軸:順列度数-X軸:対数頻度区間,

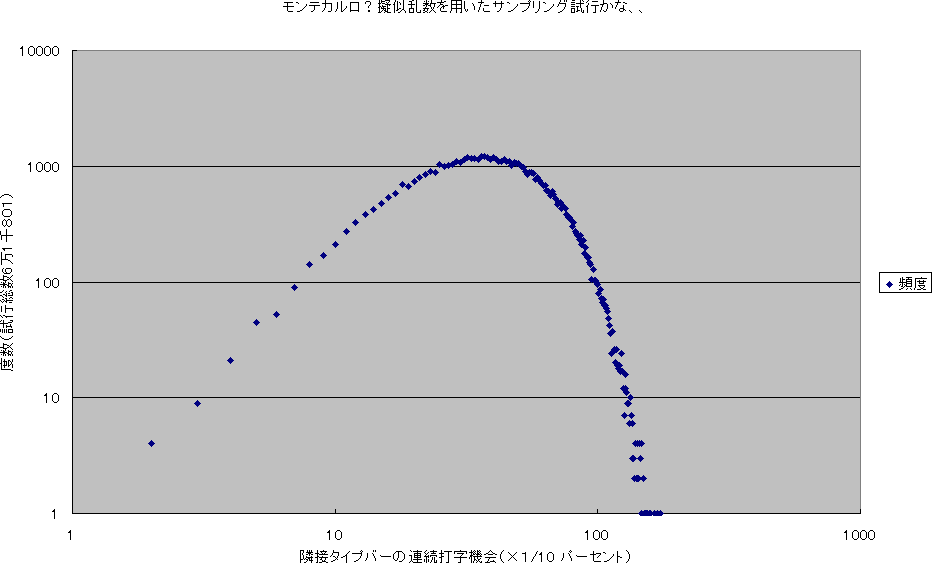
 Y軸:対数順列度数-X軸:対数頻度区間,
Y軸:対数順列度数-X軸:対数頻度区間,
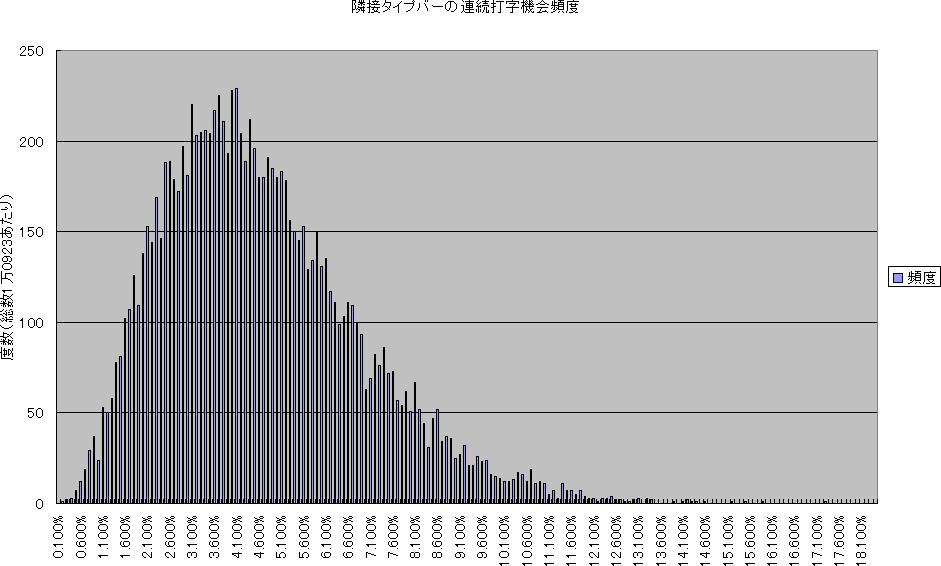


1882年版QWERTY配列でのアルファベット26文字部のランダムな並べ替え案を 隣接タイプバーの連続打字機会頻度で評価する。
1882年版QWERTY配列での英字26文字部の擬似乱数による代替配列案を 隣接タイプバーの連続打字機会頻度で評価する。
1882年版QWERTY配列の英字26文字部へ擬似乱数で代替配列案、隣接タイプバーの連続打字機会頻度で採点する
- ただし、
- タイプバーの並びとキーボードキー配置の間には、ディッカーソンの規則性があると仮定する。
- その場合 実際にタイプバーに隣接関係が生じるのはQWERTY配列を例に言うと AZSXDCFVGBHNJMK の15文字の並び部分である
- 大文字あるいは小文字打字操作のみとし、シフトキー操作での操作タイミングのずれは ないものとする。
- 打字頻度評価は、ブラウンコーパスを打字した時の頻度を以って行う。
現シミュレーションの問題点、
- 現在のアルゴリズムでは、対象15文字区間が同一な配列を排除していない。重複してカウントされている可能性がある。
- ソフト構成は、Excel2003でやっており、擬似乱数などworksheet関数とvbaでの繰り返しDo Loopなどで組んでいる。
サンプル数――並べ替え代替オルタナティヴ提案数――が増えるほど、分布度数の荒さが減っていくようである。1万と6万では、6万提案のほうが、分布の乱れが減り、連続曲線状になっているようである。


Y軸:順列度数-X軸:頻度区間,

 Y軸:対数順列度数-X軸:頻度区間,
Y軸:対数順列度数-X軸:頻度区間,Y軸:順列度数-X軸:対数頻度区間,

 Y軸:対数順列度数-X軸:対数頻度区間,
Y軸:対数順列度数-X軸:対数頻度区間,





タイプライターの数学・科学・技術、、キーボードの数学・科学・技術、、
http://raysci.g.hatena.ne.jp/raycy/
http://raysci.g.hatena.ne.jp/raycy/
http://www001.upp.so-net.ne.jp/isaku/rand.htmlEXCELの擬似乱数で推論進めてて大丈夫か、、OOOやGoogle docではどうか? ??
最も多くの 人に使われている乱数であろう Visual Basic の Rnd の質は最低である。
1882年QWERTY配列での英文字部文字並びを擬似サイコロの出目で決めたら、どんな隣接タイプバー連続打字機会頻度の並び案が得られるだろうか。スタンドアロンのExcel2003の擬似乱数で得た結果を Google docでpublishしてみている、、
下図は そのスナップショット

ってか、そういう問題じゃあ なさそうなことは うすうす 感ずいてはいる、、
モンテカルロ法,乱数,および疑似乱数
杉 田 洋
大阪大学大学院理学研究科数学専攻
http://homepage.mac.com/hiroshi_sugita/mcm.htmlモンテカルロ法って何でしょうか?
モンテカルロ法では問題に応じて確率空間 ---
モンテカルロ法の目的は S の一般的な値(Sのとりうる値のうちで例外的でない値)をサンプリングすることです.--- と,その上で定義された確率変数 S を設定します.
- 確率空間
- 簡単のため,L 回の硬貨投げの確率空間
( {0,1}L, PL = 一様確率測度 ) としますここでは L=100,000,000,すなわち S は ω∈{0,1}100,000,000 の関数としましょう.
- サンプリング
- ω を一つ選んで S(ω) の値を求めることをサンプリング(標本抽出)といいます.
http://fe.math.kobe-u.ac.jp/Movies/cm/2008-01-10-cm08-sugita.html
講演: 杉田洋
内容: モンテカルロ法, 乱数, および疑似乱数
予備知識:
形式: QuickTime (Version 7以上)
ソース: 計算による数理科学の展開 2008 (2008-01-10 から 01-11, 神戸大学)
講義資料のダウンロード (PDF)
スライド
講義映像[111-1]
- カテゴリーを、視聴メモとするか、聴講メモとするか、迷う。カテゴリをLiveとするか、Archive とするか か?
- Live on air
Archve on demand
計算機が出せるのは擬似乱数だけだという、、
計算機は熱雑音とか観測するメカは 持てないもんかな、、クロックが既に歪んでいるから、持っているクロックでは、熱雑音を測れないのかな?電圧電位やらの変動ではどうか、、一様乱数にならないのかな、、 トレンドがあるとか、、
実用数値計算が、収束する関数を扱っているからだろうか、 もっぱら 一般的な値のほうに 着目してるっぽいかなあ、、
ショールズらが目指したのは、人為的に、言語の持つ統計的出現確率傾向を取り入れて あるいは試行錯誤して 急く(せく)打鍵要求に対峙 対策して 例外的な値の達成に成功した
ビデオアーカイヴ視聴メモ
大数の法則、チェビシェフの不等式、、
圧縮できないのが 乱数だ、、 ?
圧縮できるのであれば、何らかの規則性がある、、
展開アルゴリズムとの兼ね合い、、