NHK-TV番組「ダーウインが来た」(2015年1月11日)より。
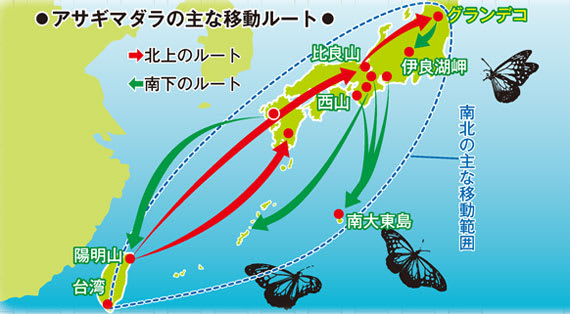
日本列島2000kmを春と秋に縦断するチョウ(アサギマダラ)の生態



番組では「NHKのマーキング作業によって春には一日で風下に向けて80km移動すること、
秋には73日かけて風上に1420km移動したことが確認された。」とあった。
そこでアサギマダラの生態から定点滞空飛行の可能性について検討してみた。
風上に向かって下降し、風下に向かって上昇しているので「ソアリング」と呼ばれる飛行とは
逆の飛行である。アサギマダラの場合は上昇気流に乗って上昇しているとのことである。
季節による風の強さ、方向、高度などの条件と、上昇気流の存在が必須であるからそれらの
条件によって滞空の範囲は異なるであろう。

ところでチョウの飛行姿を見ると(下図)翼の断面は紙のように薄い。

これは抗力が非常に小さいことを示している。滑空比は揚力と抗力の比によって決まるから
グライダーの50よりは大きな値であることはこの写真から容易に想像される。
仮に滑空比80とすれば、100mの下降で風上には8000m進むことができる。
上昇気流によって100m上昇するのはチョウにとっても十分に現実味のある数字である。
チョウは十分に軽量なので、一旦上昇気流に乗れば、上昇のためのエネルギー消費はほとんど
ない状態でこの飛行が可能である。
一方、風上への飛行は滑空を使う。無動力のグライダーが飛行するように、位置エネルギーの
放出で飛行するため、エネルギー消費はない。
2000km程の飛行をすると聞くと、相当量のエネルギーが必要と思われるのだが、実際には
上昇気流さえ見つけられれば、チョウにとってほとんどエネルギーの消費はないことが分かる。

 滑空飛行のアサギマダラ
滑空飛行のアサギマダラ
さて番組によれば、風上には73日かけて1420kmの距離を滑空しながら進んだとある。
よって、一日あたりの移動距離はおよそ20kmである。
また風下には24時間で80kmであるから、6時間で20kmの移動である。
従って風下に6時間の上昇飛行と空気流一体での飛行をし、風上には24時間飛行で、
滑空下降のサイクルとすれば、それを反復することで、およそ20kmの範囲でエネルギー
消費無しに、定点滞空の可能性がある。
一方、上昇と下降の反復サイクルは、上昇気流による上昇高度と、滑空比による下降移動に
よって変化する。今仮に滑空比80と仮定し、一回当たりの上昇高度が120mで、尚且つ、
水平移動距離の範囲を20km以内とした場合では、2回の滑空が必要であるから、その間で
2回の上昇が必要となる。1回あたりの上昇高度が高いほど、上昇サイクルは少なくなる。
従って上昇高度によって、上昇下降のサイクル回数が決まる。
アサギマダラの渡り条件下での上昇と下降の反復滞空サイクル
風下移動は6時間、風上滑空移動の方では24時間のインタバルサイクル

チョウのような軽量動物だけが、こうした飛行が可能なのかもしれない。
しかしアサギマダラの渡りが教えてくれるのは、紙飛行機のような昆虫が、僅かなエネルギーで
季節風に向かって1000km以上も移動することが可能であるという事だ。
鳥類でも渡り鳥のように長距離を移動する動物が知られている。アサギマダラと同様に、
上昇気流と滑空を使っての飛行をすればエネルギーの消費は少なくて済みそうであるが、
チョウとは違い重量があるため、上昇気流に乗るまでには相当量のエネルギーは必要と
思われる。

渡り鳥の場合はエネルギーを蓄える特殊な生化学反応を使っていると聞く。
エネルギー消費が少なくて、且つ上昇気流のない成層圏での滞空飛行を実現する
ためには、チョウのように抗力が少なく、且つ揚力は十分大きい薄断面翼を
持った構造が必須であろう。
写真右から分かるようにチョウは全翼機構造で、且つ複葉(4枚翼)となっていて、
長距離飛行にとって全く無駄のない構造だ。正しく自然の姿は理想的で美しい。
日本列島2000kmを春と秋に縦断するチョウ(アサギマダラ)の生態



番組では「NHKのマーキング作業によって春には一日で風下に向けて80km移動すること、
秋には73日かけて風上に1420km移動したことが確認された。」とあった。

そこでアサギマダラの生態から定点滞空飛行の可能性について検討してみた。
風上に向かって下降し、風下に向かって上昇しているので「ソアリング」と呼ばれる飛行とは
逆の飛行である。アサギマダラの場合は上昇気流に乗って上昇しているとのことである。
季節による風の強さ、方向、高度などの条件と、上昇気流の存在が必須であるからそれらの
条件によって滞空の範囲は異なるであろう。

ところでチョウの飛行姿を見ると(下図)翼の断面は紙のように薄い。

これは抗力が非常に小さいことを示している。滑空比は揚力と抗力の比によって決まるから
グライダーの50よりは大きな値であることはこの写真から容易に想像される。
仮に滑空比80とすれば、100mの下降で風上には8000m進むことができる。
上昇気流によって100m上昇するのはチョウにとっても十分に現実味のある数字である。
チョウは十分に軽量なので、一旦上昇気流に乗れば、上昇のためのエネルギー消費はほとんど
ない状態でこの飛行が可能である。
一方、風上への飛行は滑空を使う。無動力のグライダーが飛行するように、位置エネルギーの
放出で飛行するため、エネルギー消費はない。
2000km程の飛行をすると聞くと、相当量のエネルギーが必要と思われるのだが、実際には
上昇気流さえ見つけられれば、チョウにとってほとんどエネルギーの消費はないことが分かる。

 滑空飛行のアサギマダラ
滑空飛行のアサギマダラ さて番組によれば、風上には73日かけて1420kmの距離を滑空しながら進んだとある。
よって、一日あたりの移動距離はおよそ20kmである。
また風下には24時間で80kmであるから、6時間で20kmの移動である。
従って風下に6時間の上昇飛行と空気流一体での飛行をし、風上には24時間飛行で、
滑空下降のサイクルとすれば、それを反復することで、およそ20kmの範囲でエネルギー
消費無しに、定点滞空の可能性がある。
一方、上昇と下降の反復サイクルは、上昇気流による上昇高度と、滑空比による下降移動に
よって変化する。今仮に滑空比80と仮定し、一回当たりの上昇高度が120mで、尚且つ、
水平移動距離の範囲を20km以内とした場合では、2回の滑空が必要であるから、その間で
2回の上昇が必要となる。1回あたりの上昇高度が高いほど、上昇サイクルは少なくなる。
従って上昇高度によって、上昇下降のサイクル回数が決まる。
アサギマダラの渡り条件下での上昇と下降の反復滞空サイクル
風下移動は6時間、風上滑空移動の方では24時間のインタバルサイクル

チョウのような軽量動物だけが、こうした飛行が可能なのかもしれない。
しかしアサギマダラの渡りが教えてくれるのは、紙飛行機のような昆虫が、僅かなエネルギーで
季節風に向かって1000km以上も移動することが可能であるという事だ。
鳥類でも渡り鳥のように長距離を移動する動物が知られている。アサギマダラと同様に、
上昇気流と滑空を使っての飛行をすればエネルギーの消費は少なくて済みそうであるが、
チョウとは違い重量があるため、上昇気流に乗るまでには相当量のエネルギーは必要と
思われる。

渡り鳥の場合はエネルギーを蓄える特殊な生化学反応を使っていると聞く。
エネルギー消費が少なくて、且つ上昇気流のない成層圏での滞空飛行を実現する
ためには、チョウのように抗力が少なく、且つ揚力は十分大きい薄断面翼を
持った構造が必須であろう。
写真右から分かるようにチョウは全翼機構造で、且つ複葉(4枚翼)となっていて、
長距離飛行にとって全く無駄のない構造だ。正しく自然の姿は理想的で美しい。















