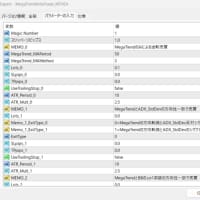
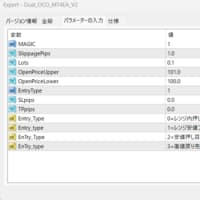
石原順(西山孝四郎)講師の順張り新ボラティリティ戦略の基本となるインジケータであるMegaTrendFollowが長期トレンドの方向性判断に利用されるHMA(Hull Moving Average)が基準となっていることが判明し、その移動平均の期間は50であり、移動平均の計算方法は単純移動平均(SMA)であることが確定した。
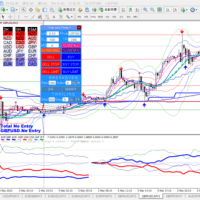
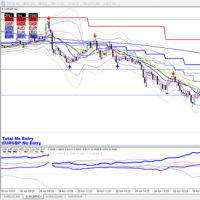
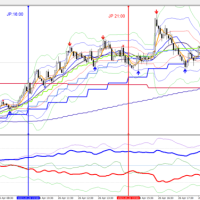
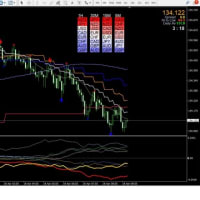
筆者作成のEAにて講師のデフォルトのパラメータにて、バックテストを試みた結果を示しておきたい。通貨ペア:EURUSDの日足、期間;2021.01.01 ~ 2021.11.30


なんともおぞましい結果となった。チャートの矢印の位置に着目すると売りも買いも反応が遅すぎるのである。
筆者が採用したHMAの期間は、最初はインジケータ(HMA)のデフォルト通り、期間は144、移動平均の計算方法は線形加重移動平均(LWMA)としていた。講師のインジケータとパラメータが解明されたからには、まず講師の設定を尊重してこれを基準として、その後、最適組み合わせを適宜考えればよいと判断し、先ずは講師の設定でテストを行ったわけである。
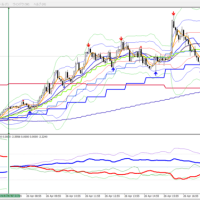
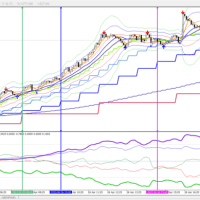
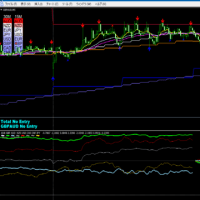
でも、のっけからこのような結果は困ったものである。そこで、移動平均の計算方法をSMAからLWMAにパラメータ変更をして行ったバックテストは次の通りであった。


明らかに売買シグナルの点灯は早くなった。バックテストの結果も、PFは1.54とまず満足のいくものであるし、レバレッジ3程度の安全運用に徹すれば、年率10%超にはなる。少額途転取引としては合格であろう。
因みに、当初の期間144、計算方法LWMAではPF 3.16 純利益は33,562円となった。トレード回数が3と極端に少なくなることと、ADXやStdDevとの相性考えると、本戦略の基本的な組み合わせは、期間50とLWMAに落ち着くのではないかとの結論である。
次回は、次のステップであるMegaTrendFollow同方向の(ADX_StdDev)シグナル点灯での増玉のテストを行いたい。