前の記事「時刻の非同時性」の主眼は、高速移動物体の空間表現がローレンツ収縮ではなく、ローレンツ伸張であるのを示すことにあった。結果的に、時刻ゼロのタイミングで光源が実際の空間的位置からずれるという不思議な状態を、課題として残した。また移動慣性系の中心から発した光の両端への同時到達を説明できても、両端以外の中間点での時刻の非同時性を放置している。今回の記事では、それらの課題の解決を目指す。
⑧ 空間伸張+時間遅延で捉えた時刻の非同時性補正
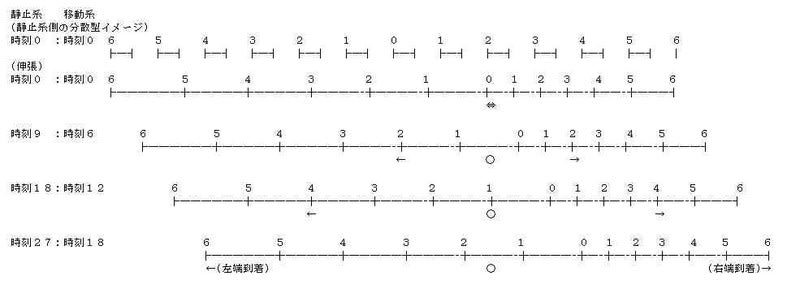
記事「時刻の非同時性」では、特殊相対性理論で説明される時刻の非同時性を説明するために、最終的に下記図の高速移動物体のローレンツ伸張イメージに辿り着いた。下記図では、移動慣性系の内外で光速が同一のままに、移動慣性系の両端6に光が到達している。しかしよくよく見ると、その到達時刻の前で光は、移動慣性系の光源から異なる距離にいる。例えば静止系時刻18での光は、移動慣性系の左側座標4の手前にいるが、右側座標4を越えている。つまり両方向に進んでいる光は、両端6の同時到達を目指すだけで、中間地点の同時到達を実現していない。
※下記図では、移動慣性系と静止系の空間中心点となるゼロ座標が、時刻ゼロのタイミングで既に慣性系間でずれている。ただし移動慣性系の空間伸縮がある場合、このずれは必ず発生する。しかし前の記事での時刻ゼロのタイミングの空間圧縮ケースと違い、空間伸張では移動慣性系の進行位置の後退が起きない。またここでは、移動慣性系の中心にある光源から発せられた光が、光源から等距離にある移動慣性系の全地点に同時到着するのを目指す。したがって以下でも、両慣性系の空間中心点のこのようなずれを、問題にしない。
※上記図の説明は、前の記事「時刻の非同時性」を参照せよ。
⑨ ⑧の中間地点における時刻の非同時性補正
もちろん中間地点4の同時到達を目指すのなら、上記図と同じような下記図を描くことが出来る。
最初の図で移動慣性系の両端6に光が同時到達したように、上記図で移動慣性系の中間地点4に光が同時到達している。しかし最初の図と上記図では、光源のずれる位置が異なる。しかも上記図でも、中間地点4に到達する前の光は、相変わらず移動慣性系の光源から異なる距離を進行している。例えば静止系時刻9での光は、移動慣性系の左側空間座標1にいるが、右側空間座標2を越えている。つまり両方向に進んでいる光は、中間地点4の同時到達を目指すだけで、相変わらずさらなる中間地点の同時到達を実現していない。
⑩ ⑧の全中間地点における時刻の非同時性補正(新バージョンのガリレオ変換)
もし全ての中間地点の同時到達の実現を目指そうとすれば、今度は時間進行に応じて光源がずれてゆくという新たな想定が登場する。しかしこの想定の可否は、光源から等距離にある移動慣性系の各地点への同時到達を実現するための随時な光源移動の可否にかかっている。ところが移動慣性系の座標0、座標2、座標4、座標6の同時到達を実現するための随時な光源移動を加えると、下記図のようになってしまう。
上記図では、移動慣性系での光源から等距離にある系内各地点への同時到達が実現している。また時刻ゼロのタイミングでの光源の実際の空間的位置からのずれも解消している。しかし静止系から見た光速は、進行方向と逆向きに減速し、進行方向と同じ向きに加速している。この座標変換はどちらかと言えば、ローレンツ変換ではなく、ガリレオ変換である。とはいえ上記図は、移動慣性系内の光速の偏差を解消している点で、ガリレオ変換とも異なる。しかしガリレオ変換と同様に、静止系から見た光速の偏差という問題を抱えている。
⑪ ローレンツ変換から外れた時刻の非同時性補正
下記図では、上記のような新バージョンのガリレオ変換を補正するために、進行方向に対して移動慣性系の空間伸張率を空間位置に応じて変更する。もともと空間伸張および時間遅延は、光速の同一性を保持するために、空間と時間の大きさを調整したものでしかない。ここでの移動慣性系内の光速の偏差を解消する方法も、全く同じである。ここでは光速が進行方向と逆向きに減速し、進行方向と同じ向きに加速するので、減速側の空間伸張率を加速側の空間伸張率より相対的に大きくなるように調整する。もちろんこの形の補正は、ミンコフスキー空間のような時空の均一な伸縮から外れてしまう。つまりローレンツ変換からの完全な逸脱となる。
ただし作図要領自体は、移動慣性系の移動速度と光の進行速度を均一に保ち、光の進行速度に応じて移動慣性系の空間上に目盛りを振るだけで良い。見てわかるように、進行方向側の伸張率が、進行方向と逆側の伸張率に上乗せされる形で移るだけである。
上記図では、移動慣性系の空間は、光源に対して進行方向の逆側で大幅に伸張する。一方で進行方向側では伸張が無い。この図は、光源から等距離にある移動慣性系の各地点に光を同時到着させるように作成されたものなので、当然ながら移動慣性系内の全中間地点における時刻の非同時性を補正し、なおかつ前出の新バージョンのガリレオ変換版のような静止系から見た光速の偏差も解消している。また時刻ゼロのタイミングでの光源の実際の空間的位置からのずれも解消している。 この結末は前出の全ての問題を解消する。つまり上述の補正を行うなら、巷に説明される時刻の非同時性も発生しないで済ませられる。具体的に言えば、移動慣性系の光源から等距離にある地点が、静止系から見ると異なる時刻にいるという不合理も発生しなくなる。しかし一方で上述の補正にしても、あまり褒められたものではない。なぜならミンコフスキー空間型の均一な空間伸縮を無視したことで、空間伸縮の同一性を失うためである。今度は、同じ空間が光源の位置に応じて伸張率を変えるという、最強の非合理が目の前に立ちはだかっている。 一方、これまでの説明では空間伸張と時間遅延は、常に相並んで現象してきた。両者の関係は同じ事柄の裏表にすぎず、光速の同一性を保持するために、空間伸張と時間遅延はセットで起きる必要があった。したがって上記に示した同じ移動慣性系上の異なる空間伸張率の偏在は、さらに同じ移動慣性系上の異なる時間遅延率の偏在を示しそうである。ところが上記図はもともと、光の進行速度の同一性を前提にして作ったものなので、ここで伸張した空間に時間遅延を加えると、今度はせっかく獲得した光の進行速度の同一性を失ってしまう。このことから上記図は、時刻の非同時性補正のさしあたりの最終形になる。 上記の予想は、高速移動慣性系の中でしか確認できない事柄であり、検証の術が無い話かもしれない。とはいえ、進行方向の逆側の光は、最後に伸張した空間から放出される。このために移動慣性系から放出される光は、進行方向の逆側で波長が長くなり、進行方向側では相対的に波長が短くなる。このことは、遠ざかる移動慣性系の放つ光の赤方偏移と近づく移動慣性系の放つ光の青方偏移という天体観測事実に合致する。
(2011/09/12)