今も昔も変わらぬ指導法。それは符号学習の(+)(-)の授業。
+と+は、(+)
-と+は、(-)
+と-は、(-)
-と-は、(+)になるので、暗記して下さい。覚えておきましょう。
少なくとも、私はこのように指導されたことを覚えています56年前の事です。
現役中学生に直接尋ねても、私と同じ指導の回答が今までのところ100%です。暗記指導でもいいじゃないですか、と言われるかも知れませんがこれが為に理解が進まなくなる生徒が多くいることを知って欲しいのです。
あなたは、大丈夫ですか? 何故か説明が出来ますか?
説明があったとすれば暗記指導法とどのように違うのか!少しばかり述べてみますと、暗記指導は主に計算テクニックにあります。これには異論が出ると思いますしかしながら説明が不足すると「勘違い」が入り込みます。特に+・-の符号ゆえ数の増減を強く意識されてしまうのです。これが勘違いの始まりで、座標の利用・グラフ図の理解・式作りの理解・(-)符号の奇数個偶数個の利用・累乗問題の理解行く行くは方程式の解き方など、繋がりのある部分が途切れてしまう作用を起こしてしまうのです。
現状分からなくなって困っている方の多くはここにあります。暗記指導で習ったもののほかの問題に繋がって行かないので、ほとほと困り数学に興味をなくし挙句は諦めてしまいます。
このような生徒を作る・作らないは指導次第と申し上げたいのです。
こうした部分で、指導法を根本的に変える必要性を訴えています。
すごく大きな「落とし穴」に先生方は沈んだままなのです。いち早く抜け出して頂ければ生徒たちが救われる事と思います。
その解決の為の方法は、今まですでに述べました「方向図」と「領域図」の説明にあります。これは実績があります。
生徒側にとっても大変理解しやすいものです。 次に続きます。乞うご期待。











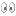
 (+4)+(-8)=
(+4)+(-8)=  (ー6)×(+5)=
(ー6)×(+5)=