本ブログ 総目次へ戻る
このカテゴリの目次へ戻る
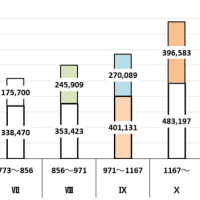
「人口動態調査 人口動態統計 確定数 出生」からグラフを作ってみた

確定数は2021年まで公表されている。1991年から31年間のグラフである。バブル崩壊後の日本経済の長期停滞期に当たる。
点線はエクセルで引いた近似曲線だ。二次関数となっており、これが重大な問題である。R2値というのは以下のとおりで、この近似曲線のR2=0.9677は未来予想としてかなり「正確」だということである。
R2乗は「決定係数」や「寄与率」と呼ばれ、回帰分析の結果得られた回帰式が目的変数の値変動をどの程度説明できているかを表す指標です。 R2乗は0〜1の値を取ります。 R2乗が1に近ければ近いほど、データに対する当てはまりが良く、回帰式の精度が高いことを意味しています。
なぜ近似曲線が二次関数となるのだろうか?
考えてみれば当たり前のことである。世代ごとに3割ずつ人口が減っていくなら二世代では0.7×0.7=0.49。元が減っているところに出生率が下がれば、掛け算でさらに減るということだ。重力加速度を思い出した人もいるかもしれない。
これは、合計特殊出生率が2を大きく超えると、人口がうなぎ上りに増え、2を大きく下回ると人口が急減するということを意味する。
グラフから見えてくるのは、今から四半世紀も経たないうちに出生数がゼロになるということだ。もちろんそんなことは起きないだろう。起きないだろうから冒頭に「今回はネタ?」と振っておいた。
2021年の合計特殊出生率は1.30である。合計特殊出生率は一人の女性が一生の間に産むも数に相当する。女性だけで、ざっくり、みると1.30÷2=0.65。35%減っていくということになる。2を大きく下回ると人口が急減するというケースである。
出生数の減り方は二次関数的である。これはかなり厳しい現実であり、政府も少子化対策を強化するようだが、その財源が以下のようでは話にならない。
「少子化対策の財源確保のため、医療保険料に上乗せして徴収する支援金の負担額について、1人あたり平均で月500円弱を見込んでいる云々」
総額で6000億円程度にしかならず、額としてお話にならないし。国民から徴収するというのでは逆効果であろう。それでなくても医療保険料は逆進性が高いのだ。
少子化対策は、考えうる最大の「未来への投資」である。未来への投資を国債発行で賄ってはならないという理屈がどこにあるのだろうか。
そして最大の少子化対策は子育て世代の所得向上であり、そのためのしっかりした需要対策なのだ。