量子コンピュータの原理の一つに
「重ね合わせ」の原理がある。
象徴的には、
電子が波でもあり粒子でもあるという
二つの状態を同時に共存していることだ。
いわばコインを空中に放り投げて、表と裏が
同時に共存している状態であって、
地上に落ちれば、裏か表かが初めて確定する。
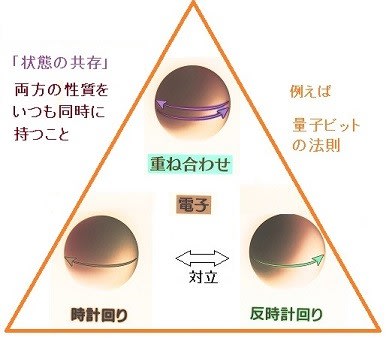
同様に量子ビットでも
時計回りと反時計回りの回転を
同時に共存する状態を使って、
重ね合わせのままで計算する。
オイラーの公式では
指数関数はSIN関数とCOS関数の
「重ね合わせ」となっている。




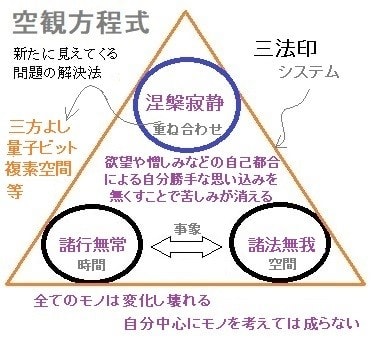
仏教での三法印においても
涅槃(悟り)と寂静(安らぎ)の二つの状態が
同時に共存していることにある。
いわば「重ね合わせ」の状態である。
涅槃=SIN関数
寂静=COS関数
そうした状態が量子ビットと同様に
問題の解決に役立っている。
空観方程式でも
両方の状態をいつも同時に持つことであり、
二つの状態の連立方程式となっている。
涅槃=空間(関係)
寂静=時間
即ち、
あるときはあるように
ないときはないように。
できないときはできないように
できるときはできるように。
戦える時は戦い、
戦えないときは戦わない。
参考:弁証論について
対立したり矛盾したりする概念の
双方を合わせ、どちらも切り捨てることなく
より高次の次元での概念を導く。
例
とんかつとカレーライスを
どちらも切り捨てることなく
高次な次元に導くと
カツカレーが生まれる。
子供に必要な勉強とゲームの場合
どちらも切り捨てることなく
高次な次元に導くと
学習ゲームが生まれる。
キリストが生誕した時の祝日名
メリークリスマスは非キリスト教徒には
当てはめられない。そこで双方の合議により
ハッピーホリデーという名称による
祝日が生まれる。
以上のような合議は止揚論として使われるが、
いずれも静的な事例や概念によるものである。
一方の
量子ビットの場合はどちらも切り捨てることなく
高次な次元に導くと「重ね合わせ」という
動的な概念として導入されている。
弁証論
「重ね合わせ」の原理がある。
象徴的には、
電子が波でもあり粒子でもあるという
二つの状態を同時に共存していることだ。
いわばコインを空中に放り投げて、表と裏が
同時に共存している状態であって、
地上に落ちれば、裏か表かが初めて確定する。
同様に量子ビットでも
時計回りと反時計回りの回転を
同時に共存する状態を使って、
重ね合わせのままで計算する。

オイラーの公式では
指数関数はSIN関数とCOS関数の
「重ね合わせ」となっている。




仏教での三法印においても
涅槃(悟り)と寂静(安らぎ)の二つの状態が
同時に共存していることにある。
いわば「重ね合わせ」の状態である。
涅槃=SIN関数
寂静=COS関数

そうした状態が量子ビットと同様に
問題の解決に役立っている。
空観方程式でも
両方の状態をいつも同時に持つことであり、
二つの状態の連立方程式となっている。
涅槃=空間(関係)
寂静=時間
即ち、
あるときはあるように
ないときはないように。
できないときはできないように
できるときはできるように。
戦える時は戦い、
戦えないときは戦わない。
参考:弁証論について
対立したり矛盾したりする概念の
双方を合わせ、どちらも切り捨てることなく
より高次の次元での概念を導く。
例
とんかつとカレーライスを
どちらも切り捨てることなく
高次な次元に導くと
カツカレーが生まれる。
子供に必要な勉強とゲームの場合
どちらも切り捨てることなく
高次な次元に導くと
学習ゲームが生まれる。
キリストが生誕した時の祝日名
メリークリスマスは非キリスト教徒には
当てはめられない。そこで双方の合議により
ハッピーホリデーという名称による
祝日が生まれる。
以上のような合議は止揚論として使われるが、
いずれも静的な事例や概念によるものである。
一方の
量子ビットの場合はどちらも切り捨てることなく
高次な次元に導くと「重ね合わせ」という
動的な概念として導入されている。
弁証論















