微分が無限者の本質を明らかにするのに対し、積分が明らかにするのは無限者の概念である。もともと無限者は、無限定を保持したままの直観的素描で限定され得ない。無限者を限定するためには、その限定を可能とする表現を通じなければいけない。限定量に対して無限定量を表現するのは、比である。比において無限定量が持つ無限定性は止揚される。ヘーゲルは比を函数に見出し、無限定量の限定を函数が可能にすると考える。ヘーゲル微分論の注釈が最後に示すのは、量から質への転化を積分の形で具現した数学史の敷衍である。すなわち積分が実現するのは、数理における無限定量の概念的確立である。それは、媒介を経た無限者の限定を表現する。
[第一巻存在論 第二篇「大きさ(量)」第二章「限定量」のC「量的無限定性」の微分法成立に関する注釈3の概要]
微分法が明らかにするのは、無限小が表現する個物の質である。それは原函数に現れる一般的で無限定な比として示された。この微分における原函数の冪次元の引き下げは、曲線から直線、曲面から平面、または面から線、立体から面への次元推移を表現する。このときに連続量としての線は点の集合へと、連続量としての面は線の集合へと分解される。このような微分と逆に、分解量から原函数を構成するのが積分である。微分と積分のいずれにおいても、低次函数と高次函数の相互推移の説明に無限小が使われてきた。しかし無限小は説明に恣意と困難を持ち込む。線の集合は面ではないし、面の集合は立体ではないからである。次元推移は質の次元の追加であり、函数において冪数の追加として現れる。それゆえにこの次元推移において、線は線であらぬものしての面へと脱自し、面は面であらぬものとして立体へと脱自する。ここで積分される線は、無限小の幅を持つ線状の面としての線形である。また積分される面は、無限小の深さを持つ面状の立体としての板形である。カヴァエリが不可分なものと呼んだこれらの線形や板形は、平行移動によって大きさが変わることは無い。したがってそれらにより構成される図形を平行移動により変形しても、その図形の大きさは変わらない。または不可分なものの大きさとの比に応じて、同じ比でその図形も大きくも小さくもなる。ただし比較単位としての不可分なものは、異なる場所に出現する場合、それらの合同と等比を証明する必要がある。もしそれが証明されなければ、不可分なものを積分したつもりで誤った面積や体積が算出される。
ヘーゲルはこれまでの注釈をまとめて、これらの目論見が無限者についての正当な規定を抽出することにあったと述べている。ヘーゲルの考えでは、無限者の規定に現れる混乱は、規定を拒否する無限者を無限者のままに規定することに由来する。有限者と無限者の非通約性は両者の質的差異に従う。有限者は限定量によって規定されるが、無限者は無限定量すなわち諸比によって自らを規定する。この諸比の全体は複次函数として示され、そこでの諸要素としての諸比は、複次函数の次元を落とした函数によって構成される。無限者の無限定性は、これらの函数における比において止揚されており、それゆえに無限者は規定可能となる。無限者が既知の低次函数によって規定される限り、その無限者は認識可能である。
1)低次函数と高次函数の相互推移
肯定的に捉えた場合、微分法における無限小は質的な大きさの規定性である。端的に言えば、この無限小が表現するのは個物の質である。ただしそれは微分計算の中では原函数に現れる一般的で無限定な比でしかない。それは質を持たない同質的な数同士の比として現れる。しかし微分において原函数の冪の次元が下げられると、そこには曲線から直線、曲面から平面、または面から線、立体から面への次元推移が起きる。このときに連続量としての線は点の集合へと、連続量としての面は線の集合へと分解される。当然ながら次に始まるのは、この分解量から原函数を積分する試みである。ただしその分解量は、対自的に規定されていなければならない。それは連続量の限界から対自的規定を目指し、収束に満足するだけの旧来の方法と導出の向きが反対である。しかし両方法が得る結果に差異は無い。アルキメデスが実測で得た円面積の計算式に対し、ケプラーは円周長2πrを底辺とし、半径rを高さとする三角形の総面積に捉え、円面積をπr2として導出した。これは絵柄にすると次のような円の分解と積分を意味する。

ヘーゲルは、このケプラーによる上記の円面積の導出を積分の最初のケースとして評価している。ただし点の集合が線になることはなく、線の集合が面になることはない。ヘーゲルの理解では、ここでの点の集合はもともと線であり、線の集合はもともと面である。
2)次元の相互推移と無限小
低次函数と高次函数の相互推移の説明では、無限小を使うのが便利である。無限小において線は点に推移し、面は線に推移すると考えられるからである。ここでの低次函数から高次函数への推移は、例えば点の線への脱自、または線の面への脱自、さらには面の立体への脱自、および立体から時空存在への脱自として現れる。いずれにおいても推移する自己は、集積において元の自己を脱する。

しかし以前の注釈で見たように、この無限小は説明に恣意と困難を持ち込む。この説明の困難は、もともと分解量同士の乗算において起きている。例えば線と線の乗算結果を面として捉えるのは既に不可解である。ここでは乗算される線と乗算する線は、どちらかが線の個数であり、どちらかが既に面でなければいけない。複数の線は、やはり線であり面ではないからである。したがってもともとここに推移は無い。これらの脱自は、既存の次元に対する新たな一次元の乗算である。既存の次元が表現するのは新たな次元における単位であり、新たな次元が表現するのは既存の次元の個数である。そしてこれらの次元の総数は、函数において冪数として現れる。したがってそれらの脱自は、既存の冪数に対する加算でもある。もちろんこの冪数の加算は、次元の乗算を内に含む。また既存の次元は、対象における質の次元でもある。当然ながら上記の脱自は、既存の質の次元に新たな質の次元を追加する。例えば既存の次元が縦幅と横幅の二つの質であるなら、新たな次元の追加は対象に新たな質として奥行きを与える。一方で脱自が冪を伴うのであれば、一次元の線の冪が二次元の面に推移するように、二次元の面の冪は四次元の存在へと推移すべきである。ここでの面の四次元存在への推移は、面を三次元に収まりきれない算術的存在へと脱自させる。その脱自が表現するのは、動態にある対象の自由な運動である。この脱自との比較で言えば、二次元の面の三次元の立体への推移は、面を静的な幾何学的な空間存在へと脱自させるだけに留まる。
3)不可分なものの集積と比率
線を無限小の幅を持つ面として捉える場合、長方形の面積は一つの辺に平行な線を高さの分だけ積分した大きさとして現れる。しかし大きさの無い線を積分しても面積を得られない。ここで積分される線は、無限小の幅を持つ線状の面としての線形である。カヴァエリはそれを不可分なものと呼んでいる。カヴァエリは、この線形の大きさが平行移動によって変わらないことに注目する。すなわちそれは、一つの辺を底辺として固定し、全ての底辺に平行な線形を平行移動し、四角形を平行四辺形に変形しても、その高さが変わらなければ面積が変わらないのを示す。当然ながら三角形を含む多角形にしても、底辺から見た各高さの平行する線形長に差異が無ければ、それらの面積が変わらない。

さらにカヴァエリは、同じ理屈が立方体や錐体の体積について成立することにも言及する。面を無限小の深さを持つ立体と捉えるなら、立体の底面を固定し、全ての平行な面を平行移動しても、立体の高さが変わらなければ、その立体の体積も変わらない。この場合に不可分なものは、無限小の高さを持つ板形の立体として現れる。
ここでの二つの図形の面積の不変性は、二つの図形における線形や板形の大きさが双方の対応部分で等しいことに由来する。それゆえに二つの図形における不可分なものの大きさが双方の対応部分で等しい比率にあれば、両者の大きさの比もこの比率に従うことになる。そこで次のような楕円の面積も、円の直径に対する楕円の短径の比率OA:OBに従って簡単に計算できる。楕円の長径に垂直な線形の大きさは、同じ長径を直径とする円の直径に垂直な線形の一定比の大きさだからである。

これに対して楕円に無数の台形や三角形を埋めてその無限加算により面積を求める方法は、もともと面積が次元の乗算であることを忘却した振る舞いでしかない。すなわち楕円面積を得るために無限微差を追い求める必要は無い。それと同様に不可分な線形を構成するさらなる無限小の線形を考える必要も無い。もともと二つの図形のアルキメデス式比較は可能であり、比較自体を不可能と扱うのは非合理である。それゆえにカヴァエリも、不可分なものを二つの図形の大きさの比率を示すための単なる比較単位として扱い、それを無限概念と区別している。
4)不可分なものの抽出
逆比例において一方の変数の増大は、他方の変数を減少させる。比較単位としての不可分なものは、異なる場所に出現する場合、それらの合同と等比を証明する必要がある。例えばその証明は、二つの線形として現れる不可分なものの位置関係の平行性によって示される。もし二つの不可分なものの平行性が示されなければ、それらは異なる不可分なものとして区別される。そして異なる不可分なものを積分しても、算出された面積や体積は誤ったものとなる。ここでヘーゲルが示すのは、不可分なものに対するタクエの誤解をバローが正した次の事例である。タクエは円錐の表面積を円錐軸に垂直な円周長から積分すると、間違った答えに到達すると主張する。示された円錐は、次の図のように斜辺Lおよび底面円半径rで表わされたものである。右にその円錐表面を平面展開した図形を掲示した。

そしてタクエが提示した底面を除く円錐表面積は次のようなものである。
底面を除く円錐表面積=πr√(L2-r2)
上記の円錐表面積は、アルキメデスが示した該当面積(=πrL)より明らかに小さい。ここでのタクエの積分は、次のような座標イメージから算出される。
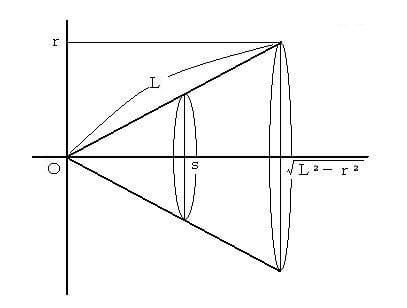
√(L2-r2)をSとして表わし、x座標sでの円周長を求めると次のような式が得られるように見える。
| x座標sでの円周長=2πr× |
| = |
|
この式をsについてx座標0からSで積分すると、底面を除く円錐表面積が次のように得られる。
| 底面を除く円錐表面積=∫0S( |
| ) |
| = |
|
=πrS=πr√(L2-r2)
そこでタクエは、次の座標イメージが正しいはずだと考え直す。

この座標イメージでx座標sの円周長を求めると次のような式が得られる。
| x座標sでの円周長=2πr× |
| = |
|
この式をsについてx座標0からLで積分すると、斜辺Lおよび底面円半径rの底面を除く円錐表面積はアルキメデスのものと一致する。
| 底面を除く円錐表面積=∫0L( |
| ) |
| = |
|
=πrL
しかし上記の座標イメージだと円錐は原型を留めずにひしゃげており、斜辺Lは円錐の高さと一致する最小値の斜辺としてのみ現れ、逆に最大値の斜辺が√(L2+4r2)として現れてくる。これを正そうと斜辺をLのままに円錐頂点を底面の中心を移動すると、今度は先の座標イメージに戻り、円錐の高さが低くなる分だけ円錐表面積も小さくなってしまう。これらの座標イメージで見ると、誤った表面積式と正当な表面積式は、座標イメージのx軸に円錐の高さを据えるか、それとも斜辺を据えるかにおいて差異を持つ。しかしいずれにおいても求められた円周は底面に平行であり、不可分なものの要件を満たす。それゆえにタクエは不可分なものの概念の妥当性そのものを疑うことになる。このことに対してバローは、不可分なものを斜辺Lに据え、ケプラーによる円面積の積分と同形式の積分で底面を除く円錐表面積を説明する。

この説明での不可分なものは、円錐底面に平行な円周のように比率から大きさを推察されたものではない。線形の全ては平行に現れる円の半径Lであり、そのまま全て合同な線形である。そこで底面を除く円錐表面積の積分式も、次のように単純化する。
底面を除く円錐表面積=∫02πr(L)=2πrL
5)無限と有限の非通約性に対する無限者の規定可能性
無限な点を通じた線の規定、または無限な線を通じた面の規定は、無限の無限定性において曖昧にされる。なぜなら無限定とは限定の否定であり、無限は規定を拒否するからである。それゆえに無限者を無限者のままに規定するのは、その規定自体が規定に混乱をもたらし、恣意的規定を醸成する。この無限の非規定性に対し、これまでのヘーゲルの注釈が狙ったのは、それらの混乱した規定の中にある正当な規定の抽出である。ここで確認されたのは、例えば直線と弧の非通約性に見られる分離されたものと連続するものの質的差異である。直線は、分離された線を結合した限定量である。それに対して弧は、分離された線を結合した無限定量である。弧はその連続性においてもともと直線としての質を持たない。その代わりに弧は自らを規定する別の諸要素に分離される。その諸要素は、弧を規定する諸比である。そしてその諸比の全体は、弧を規定する函数として示すことができる。そこでの諸要素としての諸比は、弧を規定する複次函数の次元を落とした函数になっている。それらの低次函数も、またさらに次元を落とした函数によって構成される。しかしこれらの函数では、無限定は比において止揚されている。すなわちそこでの無限者は、無限者として規定されていない。つまり不可知と思われた無限者は、諸比において白日のもとに暴かれ、少なくとも既知の低次函数によって規定可能となっている。したがって無限者の完全な規定は、その全ての低次函数を明らかにすることにおいて実現可能である。逆に言えば、無限者が既知の低次函数によって規定されるなら、その無限者は認識可能だと言われなければならない。
(2019/10/20) 続く⇒(ヘーゲル大論理学 第一巻存在論 第二篇 第三章) 前の記事⇒(ヘーゲル大論理学 第一巻存在論 第二篇 第二章Cb)
ヘーゲル大論理学 存在論 解題
1.抜け殻となった存在
2.弁証法と商品価値論
(1)直観主義の商品価値論
(2)使用価値の大きさとしての効用
(3)効用理論の一般的講評
(4)需給曲線と限界効用曲線
(5)価格主導の市場価格決定
(6)需給量主導の市場価格決定
(7)限界効用逓減法則
(8)限界効用の眩惑
ヘーゲル大論理学 存在論 要約 ・・・ 存在論の論理展開全体
緒論 ・・・ 始元存在
1編 質 1章 ・・・ 存在
2章 ・・・ 限定存在
3章 ・・・ 無限定存在
2編 量 1章・2章A/B・・・ 限定量・数・単位・外延量・内包量・目盛り
2章C ・・・ 量的無限定性
2章Ca ・・・ 注釈:微分法の成立1
2章Cb(1) ・・・ 注釈:微分法の成立2a
2章Cb(2) ・・・ 注釈:微分法の成立2b
2章Cc ・・・ 注釈:微分法の成立3
3章 ・・・ 量的比例
3編 度量 1章 ・・・ 比率的量
2章 ・・・ 現実的度量
3章 ・・・ 本質の生成















※コメント投稿者のブログIDはブログ作成者のみに通知されます