8月16日にウドンタニラジャバット大学で行われた数学競技会の各自の得点をエクセルのファイルで入手したので学校別に並び替えてみると、UP校1校の生徒の成績が飛び抜けており、私立の人気校や隣接県のトップ校の生徒は20点にも届かない。
北イサーンの中学受験ではウドンタニだけでなく、周辺県の成績が良い児童もUP校を受験し、通らなければ滑り止めに受験した私立か別の公立へ入るのでUP校が強いのは当然だが、中には日本のDQN校も驚く様なUP校の環境を嫌ってUP校へ合格しても私立へ行ったり、家庭の事情で自宅から近い中学へ通う生徒も居るので、21点以上を取って入賞するUP校以外の生徒が居ても良さそうだが、全く居なかった。
その理由を考えてみると、この様な試験は学校で勉強する範囲を超えており、学校での学習はほぼ関係無い。それなのに得点差が生じるのは、やはり塾等の校外での学習が関係しているのだろう。
ウドンタニへは中学生を対象にした数学の学習塾は多いが、多くの塾で教えるのは教科書よりやや難しいレベル。対応できるのは全国統一試験O-NETくらいまでが多い。それより上となるとバンコクの塾のビデオ配信での学習であり、リアルな講師が教える塾でO-NETを超えた受験対応となると片手で数えられる程しか無い。
ウドンタニの私立の人気校は週末や夏休みに学校で課外授業があって半強制的に参加させられるらしく、ビデオの塾以外は行き難いそうだ。その課外授業で実績を出せれば良いが、現実は思い通りに学習が進まないのではないだろうか?
ウドンタニ周辺県では、バンコクの教室と連動した大手のビデオの塾は無いし、その地域の中学校の生徒を対象にした塾では、やはり全国レベルな上位校の受験問題を解かせるのは難しそう。週末や夏休みは自家用車やバスでウドンタニへ通う生徒も居るが、人気の塾は中学校やコース別にクラス分けするのが多く、UP校理数コースの生徒だけのクラスが作ってあったり。それ以外の生徒が塾でレベルの高い学習をしようとすると、入塾した時点で既にハードルがあり分けられているのだ。
今年大学へ入った息子は、そのハードルへずっと苦しんでおり、だからこそ娘と必死に勉強してUP校理数コースへ入れたのだが・・・娘はラジャバットの試験でミス連発・・・orz
さて思い通りにならない愚痴はそのくらいにして、紹介した問題の解答。
問題
辺ABが4.5センチ、辺BCが6センチ、辺ACが7.5センチの三角形ABCがあり、辺ACに接して正方形ACDEがある。
BDの長さの二乗を求めなさい。

私はこんな図を頭に思い浮かべた。
BDの長さの二乗を求めろと言ってるので・・
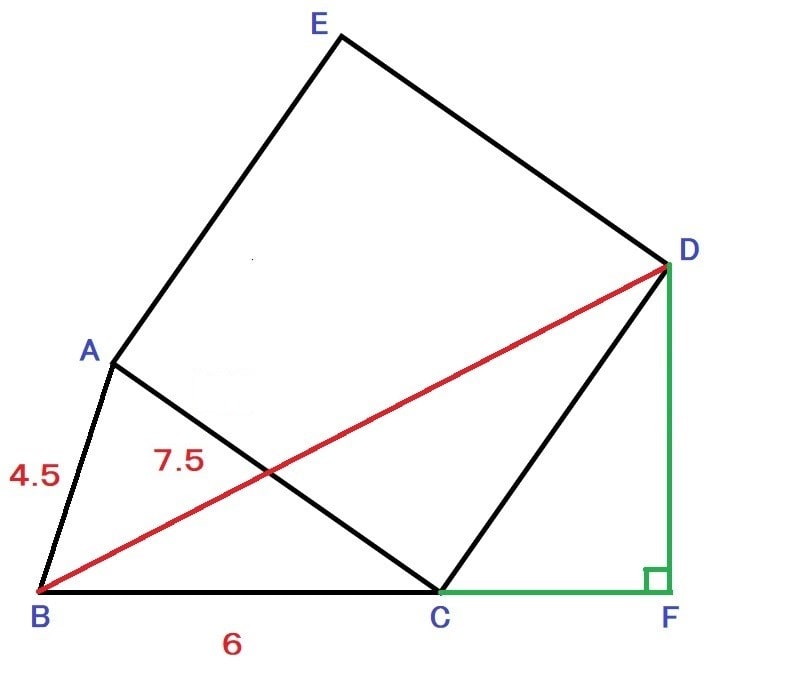
この様に直角三角形BDFを書き、ピタゴラスの定理を使ってBDの長さの二乗を求めるのではないかなと予想できる。
しかし、このままではCFやDFの長さが分からないので、少しでも情報を集める為に三角形ABCがどの様な三角形か調べる。
感が良い人は三角形ABCが直角三角形では?と思って、4.52+62=7.52に気付くだろう。
三角形ABCは下の図の様に直角三角形だ。

感が鈍い私は下の図の様に考えてxを求めてみると・・・

AG=hとして、
x2+h2=4.52 ---①
(6-x)2+h2=7.52 ---②
x2+62-12x+h2=7.52
①を②へ代入して
4.52+62-12x=7.52
20.25+36-12x=56.25
x=0
x=0となり、三角形ABCは直角三角形と判った。
AC>BCなので、三角形ABCは下の様な三角形と思う方もあるかも知れない。
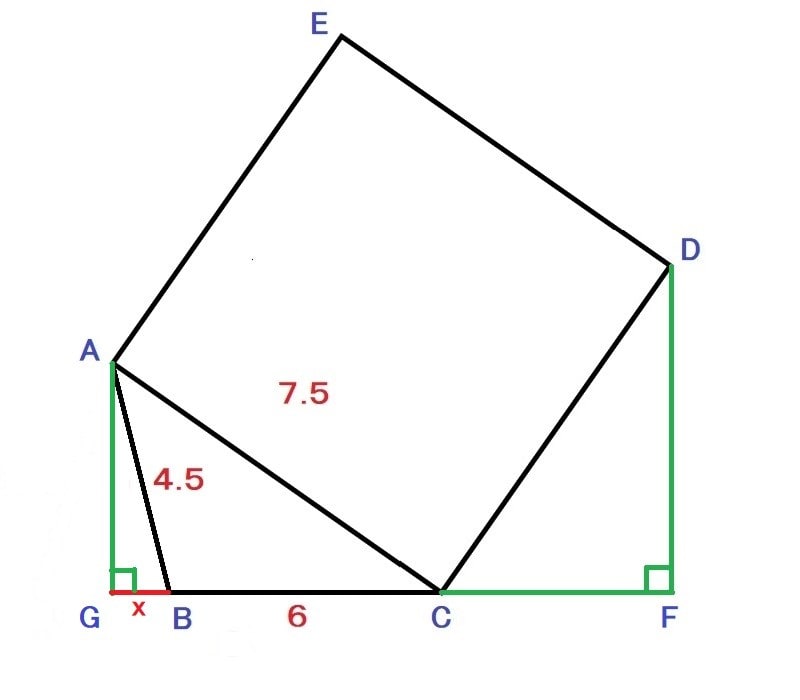
AG=hとして、
x2+h2=4.52 ---①
(6+x)2+h2=7.52 ---②
x2+62+12x+h2=7.52
①を②へ代入し
4.52+62+12x=7.52
20.25+36+12x=56.25
x=0
こちらも x=0となり、三角形ABCは直角三角形と判った。

三角形の内角の和は180°であり、∠ABCは90°なので、∠BAC+∠BCA=90°となり、
∠FCD=180°-(90°+∠BCA)=90°-∠BCA=∠BAC。
∠FDC=180°-(90°+∠FCD)=180°-(90°+∠BAC)=90°-∠BAC=∠BCA
∠BAC=∠FCD,∠BCA=∠FDC
四角形ACDEは正方形なので、AC=CD

∴ 三角形ABCと三角形CFDは、ASA (一辺両端角相等/二角夾辺相等): 1組の辺とその両端の角がそれぞれ等しいので合同。

BD2=(6+4.5)2+62=110.25+36=146.25
答え 146.25センチ
「ムガさん、解答の書き間違えだけで、解けてますね。」
長々と書いたが、
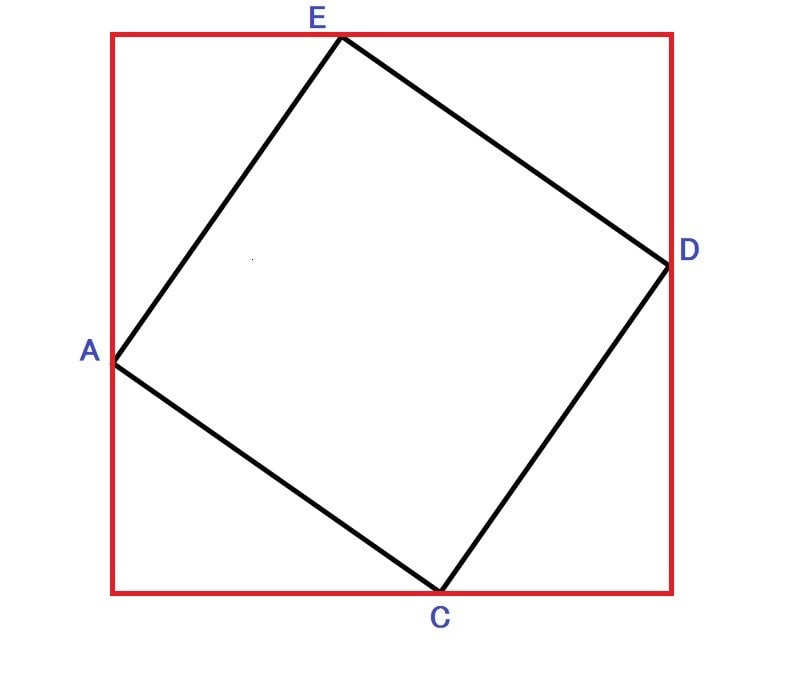
上の図の様に正方形を正方形で囲えば、周囲に出来る4つの三角形は合同なのを知っており、三角形ABCが直角三角形とスムースに気付けば簡単に解けた筈。
うちのアホ娘がどうにか解ける様にしたいが、教えても記憶に残らないし、早とちりも計算間違いも多数。なんだかもう疲れてしまった。
塾へ任せて済ませたいところだが、今回の試験で娘より成績が上の中1は、親や親族が自宅で塾のフォローをしている生徒ばかり。駄目な父親でも手を引けばもっと成績が落ちるのではないかと心配で、引くに引けない感じ。
この日曜はソオウォノ(国際ジュニア数学オリンピックの国内一次予選)。一応受験はするが、対策は全く出来てなくて気が焦るばかり。あ~あ!(ToT;)
タイの中学生向け数学ギフテッド問題の記事へのリンク→#高1入試ギフ
所詮たい焼きはたい焼きなんだからwって親の心が折れそうなw・・・
貴方のクリックとコメントが、このブログのパワーの源です。
下の2つのバナーへ応援クリックをお願いします。
 海外生活ブログ タイ情報 人気ランキングはこちら
海外生活ブログ タイ情報 人気ランキングはこちら
リアルタイムに更新される新着記事一覧(右下)からタイの今が見える。お薦め。
 タイの人気ブログが大集合!!
タイの人気ブログが大集合!!
登録数 アクセス数 最大級のブログランキング
ブログの世界が広がります。

北イサーンの中学受験ではウドンタニだけでなく、周辺県の成績が良い児童もUP校を受験し、通らなければ滑り止めに受験した私立か別の公立へ入るのでUP校が強いのは当然だが、中には日本のDQN校も驚く様なUP校の環境を嫌ってUP校へ合格しても私立へ行ったり、家庭の事情で自宅から近い中学へ通う生徒も居るので、21点以上を取って入賞するUP校以外の生徒が居ても良さそうだが、全く居なかった。
その理由を考えてみると、この様な試験は学校で勉強する範囲を超えており、学校での学習はほぼ関係無い。それなのに得点差が生じるのは、やはり塾等の校外での学習が関係しているのだろう。
ウドンタニへは中学生を対象にした数学の学習塾は多いが、多くの塾で教えるのは教科書よりやや難しいレベル。対応できるのは全国統一試験O-NETくらいまでが多い。それより上となるとバンコクの塾のビデオ配信での学習であり、リアルな講師が教える塾でO-NETを超えた受験対応となると片手で数えられる程しか無い。
ウドンタニの私立の人気校は週末や夏休みに学校で課外授業があって半強制的に参加させられるらしく、ビデオの塾以外は行き難いそうだ。その課外授業で実績を出せれば良いが、現実は思い通りに学習が進まないのではないだろうか?
ウドンタニ周辺県では、バンコクの教室と連動した大手のビデオの塾は無いし、その地域の中学校の生徒を対象にした塾では、やはり全国レベルな上位校の受験問題を解かせるのは難しそう。週末や夏休みは自家用車やバスでウドンタニへ通う生徒も居るが、人気の塾は中学校やコース別にクラス分けするのが多く、UP校理数コースの生徒だけのクラスが作ってあったり。それ以外の生徒が塾でレベルの高い学習をしようとすると、入塾した時点で既にハードルがあり分けられているのだ。
今年大学へ入った息子は、そのハードルへずっと苦しんでおり、だからこそ娘と必死に勉強してUP校理数コースへ入れたのだが・・・娘はラジャバットの試験でミス連発・・・orz
さて思い通りにならない愚痴はそのくらいにして、紹介した問題の解答。
問題
辺ABが4.5センチ、辺BCが6センチ、辺ACが7.5センチの三角形ABCがあり、辺ACに接して正方形ACDEがある。
BDの長さの二乗を求めなさい。

私はこんな図を頭に思い浮かべた。
BDの長さの二乗を求めろと言ってるので・・

この様に直角三角形BDFを書き、ピタゴラスの定理を使ってBDの長さの二乗を求めるのではないかなと予想できる。
しかし、このままではCFやDFの長さが分からないので、少しでも情報を集める為に三角形ABCがどの様な三角形か調べる。
感が良い人は三角形ABCが直角三角形では?と思って、4.52+62=7.52に気付くだろう。
三角形ABCは下の図の様に直角三角形だ。

感が鈍い私は下の図の様に考えてxを求めてみると・・・

AG=hとして、
x2+h2=4.52 ---①
(6-x)2+h2=7.52 ---②
x2+62-12x+h2=7.52
①を②へ代入して
4.52+62-12x=7.52
20.25+36-12x=56.25
x=0
x=0となり、三角形ABCは直角三角形と判った。
AC>BCなので、三角形ABCは下の様な三角形と思う方もあるかも知れない。

AG=hとして、
x2+h2=4.52 ---①
(6+x)2+h2=7.52 ---②
x2+62+12x+h2=7.52
①を②へ代入し
4.52+62+12x=7.52
20.25+36+12x=56.25
x=0
こちらも x=0となり、三角形ABCは直角三角形と判った。

三角形の内角の和は180°であり、∠ABCは90°なので、∠BAC+∠BCA=90°となり、
∠FCD=180°-(90°+∠BCA)=90°-∠BCA=∠BAC。
∠FDC=180°-(90°+∠FCD)=180°-(90°+∠BAC)=90°-∠BAC=∠BCA
∠BAC=∠FCD,∠BCA=∠FDC
四角形ACDEは正方形なので、AC=CD

∴ 三角形ABCと三角形CFDは、ASA (一辺両端角相等/二角夾辺相等): 1組の辺とその両端の角がそれぞれ等しいので合同。

BD2=(6+4.5)2+62=110.25+36=146.25
答え 146.25センチ
「ムガさん、解答の書き間違えだけで、解けてますね。」
長々と書いたが、

上の図の様に正方形を正方形で囲えば、周囲に出来る4つの三角形は合同なのを知っており、三角形ABCが直角三角形とスムースに気付けば簡単に解けた筈。
うちのアホ娘がどうにか解ける様にしたいが、教えても記憶に残らないし、早とちりも計算間違いも多数。なんだかもう疲れてしまった。
塾へ任せて済ませたいところだが、今回の試験で娘より成績が上の中1は、親や親族が自宅で塾のフォローをしている生徒ばかり。駄目な父親でも手を引けばもっと成績が落ちるのではないかと心配で、引くに引けない感じ。
この日曜はソオウォノ(国際ジュニア数学オリンピックの国内一次予選)。一応受験はするが、対策は全く出来てなくて気が焦るばかり。あ~あ!(ToT;)
タイの中学生向け数学ギフテッド問題の記事へのリンク→#高1入試ギフ
所詮たい焼きはたい焼きなんだからwって親の心が折れそうなw・・・
貴方のクリックとコメントが、このブログのパワーの源です。
下の2つのバナーへ応援クリックをお願いします。
 海外生活ブログ タイ情報 人気ランキングはこちら
海外生活ブログ タイ情報 人気ランキングはこちらリアルタイムに更新される新着記事一覧(右下)からタイの今が見える。お薦め。
 タイの人気ブログが大集合!!
タイの人気ブログが大集合!!登録数 アクセス数 最大級のブログランキング
ブログの世界が広がります。






















