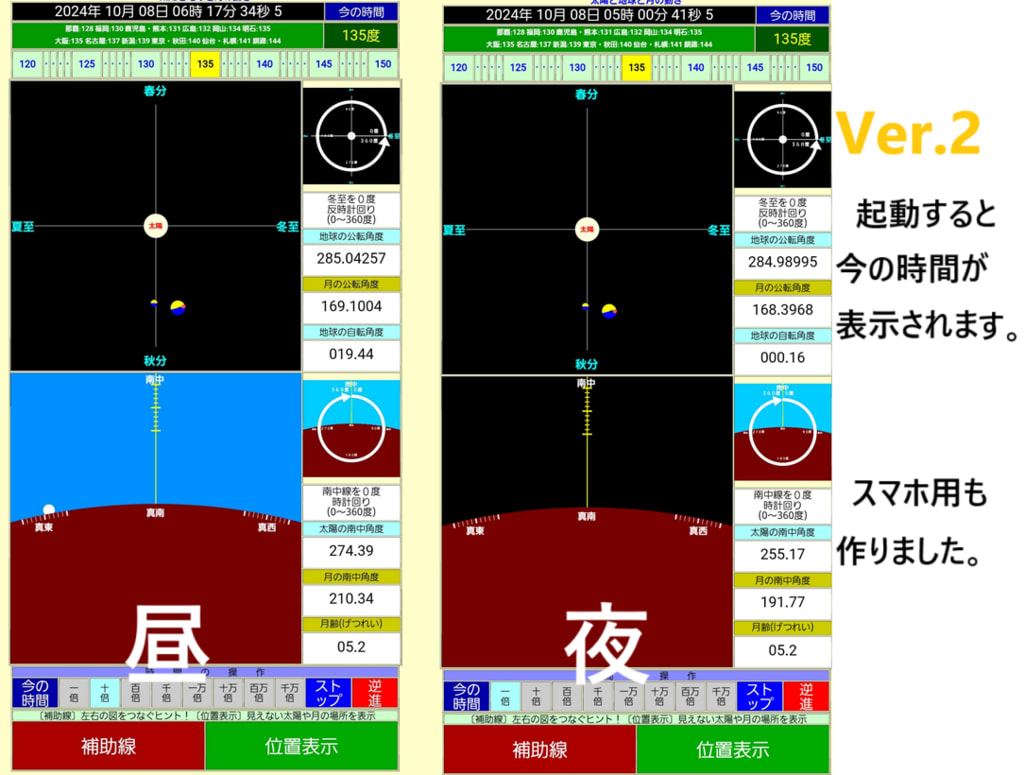
先に太陽系を示して、そこでの月の動きと日本の各地から見える月の動きと満ち欠けをシミュレーションとして提供しましたが、まだまだ一足飛びな理解を求めている教材ではないかと考えるに至りました。
そこで、その前の段階としての教材を作成しました。太陽と地球を固定して、そこで月が地球の周りを公転するときに、地球から見える月の満ち欠けを示しました。
月の満ち欠けは、同じ日時であれば、地球のどこから見ても同じですからこういう表現ができます。
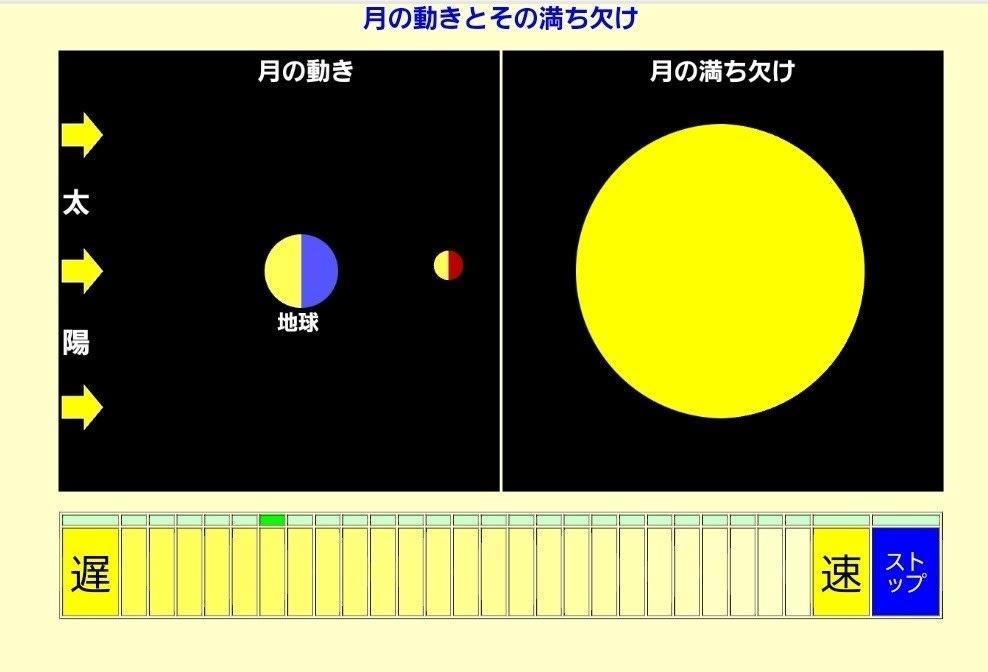
満月↑
こんな感じです。シミュレーションですから、初期設定で、月はわずかに反時計回りに動いています。下の緑の表示がありますが、これが速さを示しています。これより左側を押すと〈遅く〉なり、右側を押すと〈速く〉なります。
満月からの月の動きを順に観察していくと、
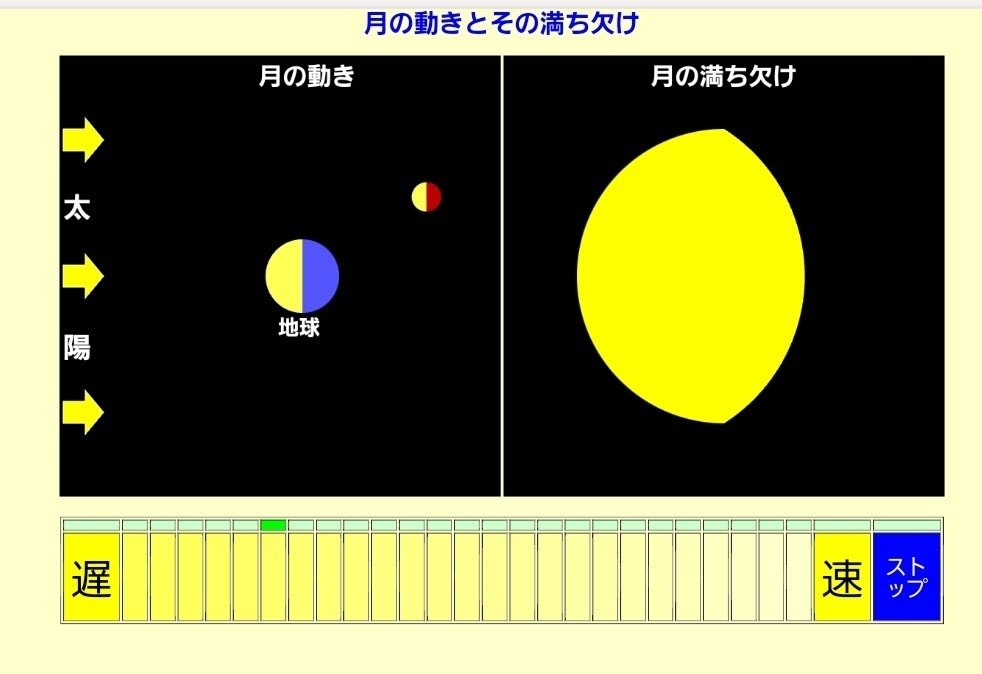

下弦の月↑

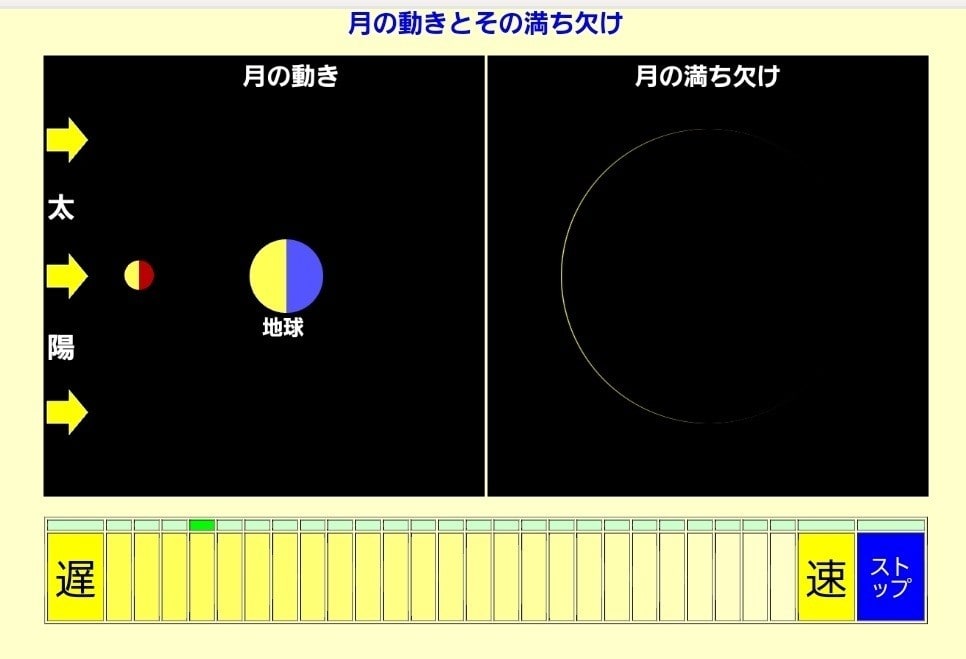
ほぼ新月↑
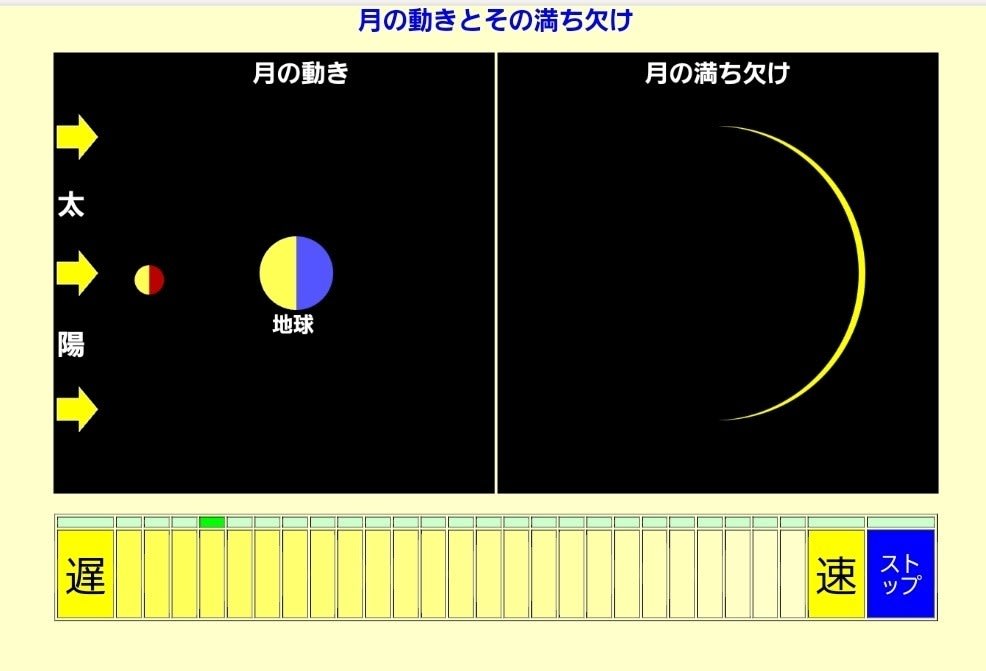
ほぼ新月↑


上弦の月↑
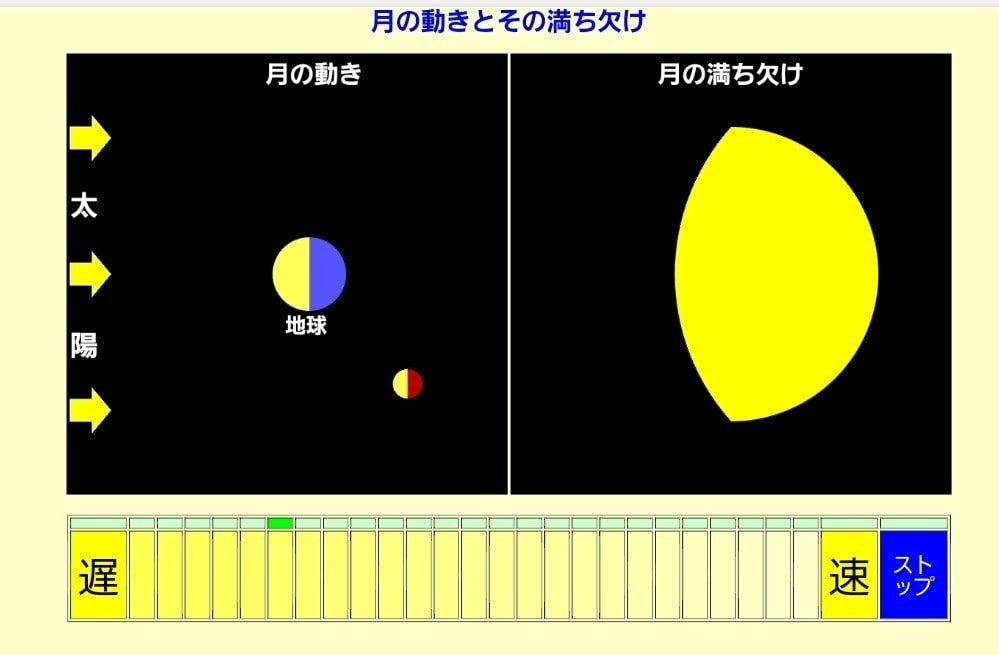
このように、月の位置によって、満ち欠けを連続的に観察することができます。
このシミュレーションからわかったことは、まず地球から見て月が太陽の反対の位置にあるときに“満月”になります。この図で月が上にあるとき、左側が明るい半月になります。その間は、満月から右側から影が広がっていく様子が観察できます。
更に時間が進むと、右側からの影の広がりが進んで、月が太陽側にきたとき“新月”となって、影が月を覆ってしまって見えなくなります。
その後は、右側から明るい部分が広がっていって、反対側に来るときは“満月”に戻ります。これを繰り返します。
太陰暦では,新月から新月までがひと月です。日数にして約29.5日です。一年は12月ですから、これでは季節がズレてします。これを修正するために、3年毎に12月の後に閏月(うるうつき)が追加されます。したがって閏月のある年は13ヶ月となります。
ニュースで中国の旧正月が紹介されますが、そのとき(太陰暦の一月一日)の満ち欠けは“新月”です。
ネットから
仕組み
- 太陰暦の1年は約354日で、太陽暦の1年(約365.24日)と比べて11日ほど短いです。<svg focusable="false" xmlns="http://www.w3.org/2000/svg" viewBox="0 0 24 24"><path d="M3.9 12c0-1.71 1.39-3.1 3.1-3.1h4V7H7c-2.76 0-5 2.24-5 5s2.24 5 5 5h4v-1.9H7c-1.71 0-3.1-1.39-3.1-3.1zM8 13h8v-2H8v2zm9-6h-4v1.9h4c1.71 0 3.1 1.39 3.1 3.1s-1.39 3.1-3.1 3.1h-4V17h4c2.76 0 5-2.24 5-5s-2.24-5-5-5z"></path></svg>
- この差を補正するために、約3年に1度うるう月を挿入します。<svg focusable="false" xmlns="http://www.w3.org/2000/svg" viewBox="0 0 24 24"><path d="M3.9 12c0-1.71 1.39-3.1 3.1-3.1h4V7H7c-2.76 0-5 2.24-5 5s2.24 5 5 5h4v-1.9H7c-1.71 0-3.1-1.39-3.1-3.1zM8 13h8v-2H8v2zm9-6h-4v1.9h4c1.71 0 3.1 1.39 3.1 3.1s-1.39 3.1-3.1 3.1h-4V17h4c2.76 0 5-2.24 5-5s-2.24-5-5-5z"></path></svg>
- うるう月の日数は29日か30日で一定ではありません。
スマホ用に、2つの図を縦に並べて細長くしたものを作成しました。

実際に使ってみませんか。次のURLかバナー(図)をタップすると使用することができます。
パソコン用です。
スマホ用です。
最後まで読んでいただきありがとうございました。
自分ながら使い勝手の良い”理解しやすい教材”ができました。
お近くに理科の先生がおられましたら紹介していただくと嬉しいです。
「動く教材」を検索してもらうと、これまで紹介したものがたくさん表示されるようになりました。皆さんに使ってもらうと、検索の上位に表示されるようになりますのでよろしくお願いします。
日本中の小中高の学校で使ってもらえたらいいな~。