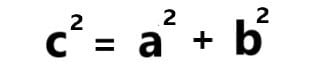「三平方の定理」は、中学校3年数学で学習する内容です。一般的には「ピタゴラスの定理」ともいいます。実際に斜辺の長さを求めるときには √ (ルート)を使いますから、3年生の最後の最後に学ぶ教材です。
直角三角形の底辺の長さをa、縦辺の長さをb、斜辺の長さをcとすると、
という式になるのが「三平方の定理」です。
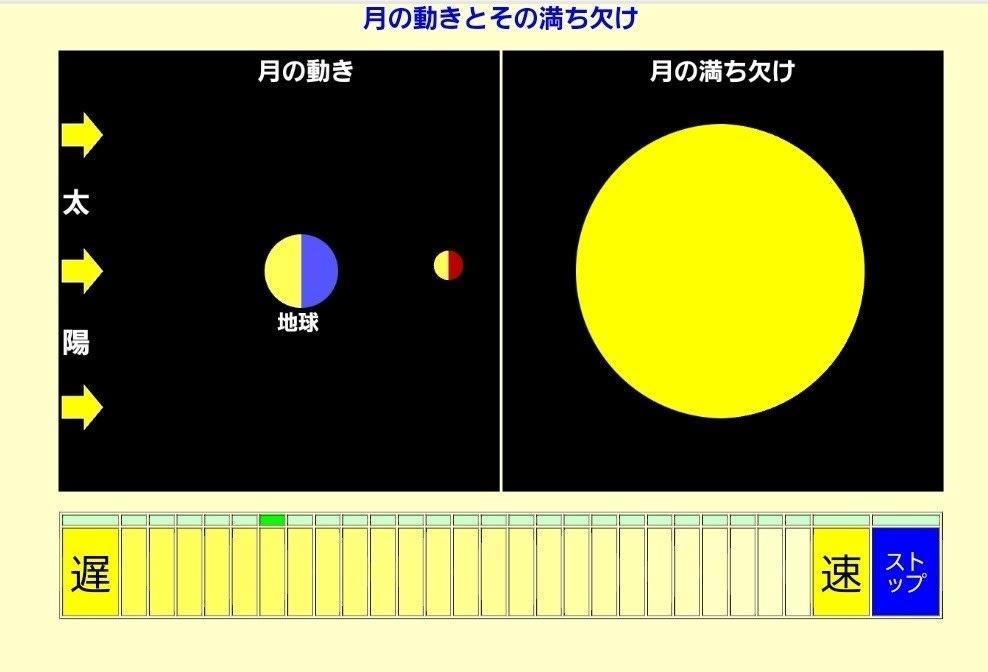
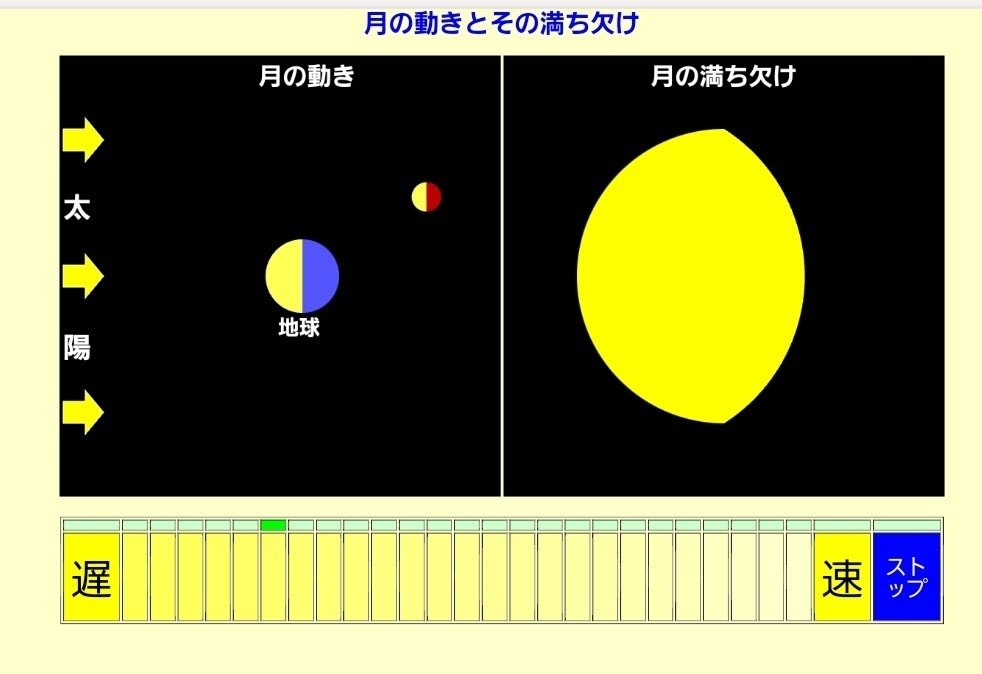
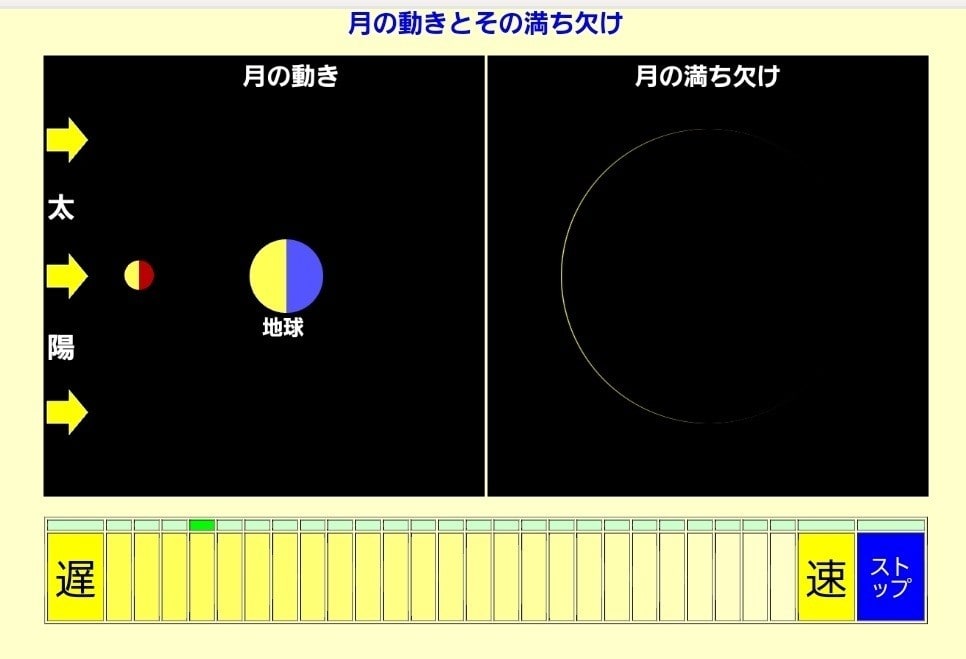
どのような動く教材かというと、直角三角形の直角を作る2つの辺、底辺と縦辺の長さを変えることができます。
それにしたがって直角三角形が変化します。もちろん斜辺の長さが変化しますから、その長さを測定するような仕組みになっています。
それぞれの辺の2乗が出てきますが、この値はそれぞれの辺を一辺とする正方形の面積にあたります。正方形を描いたり面積を求めることもできます。
三平方の定理には100以上もの証明方法があるといわれていますが、ここでも証明例を一つ紹介します。
ピタゴラスが三平方の定理を発見する過程をたどる学習です。
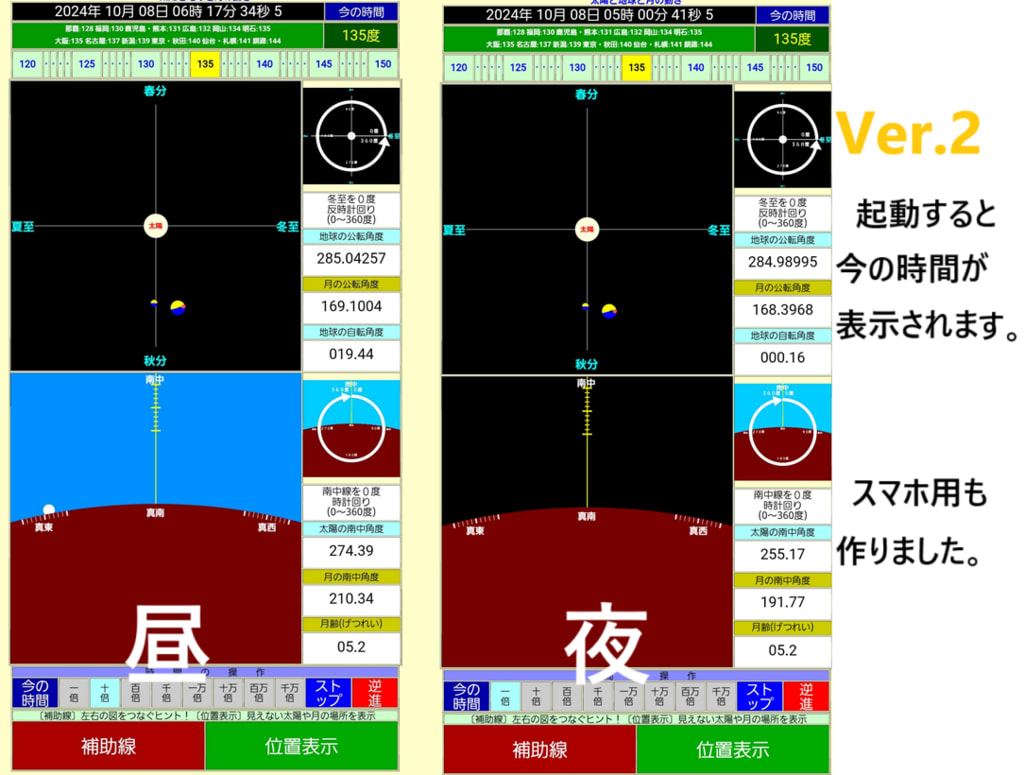
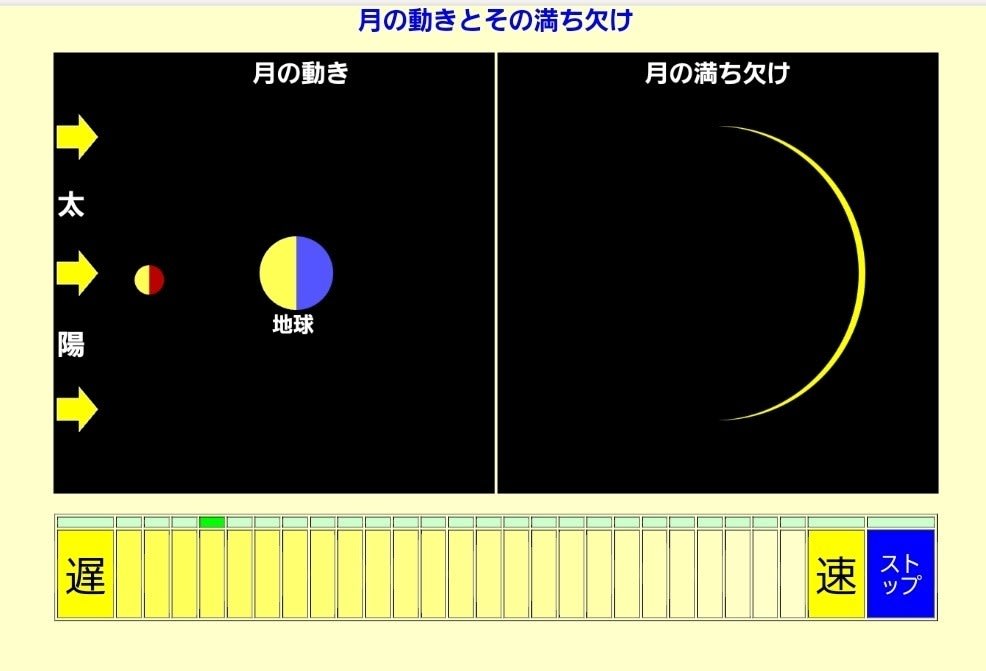
実際の画面です。
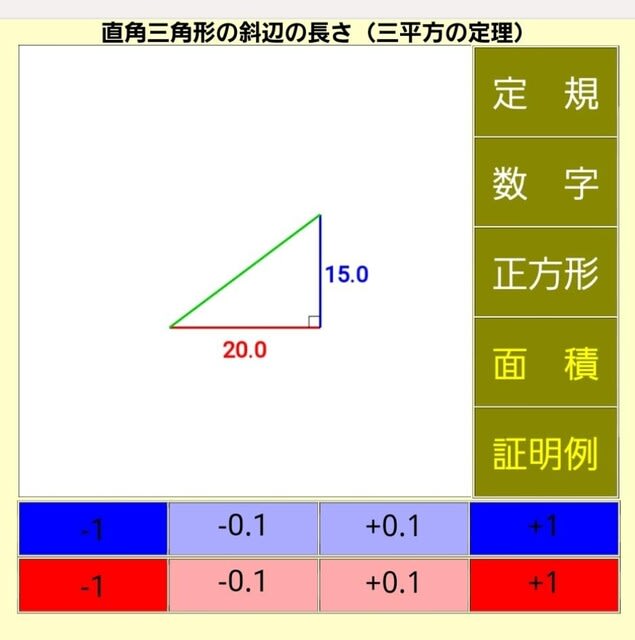
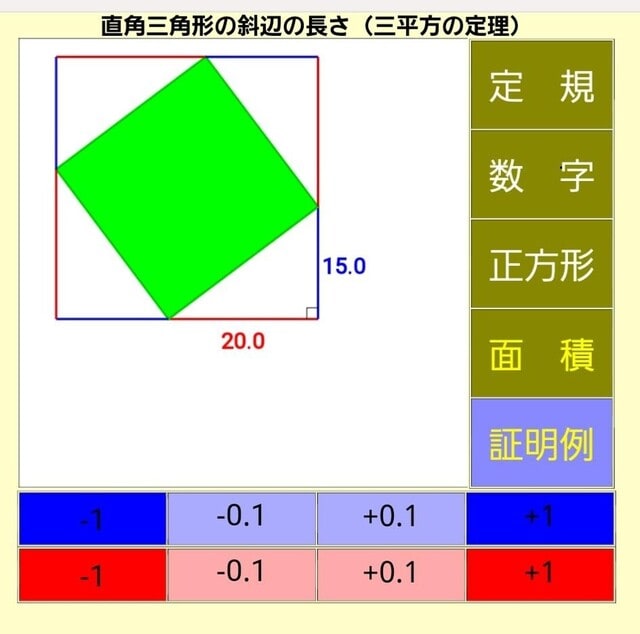
初期画面です。
底辺が20.0 縦の辺が15.0の直角三角形が描かれています。
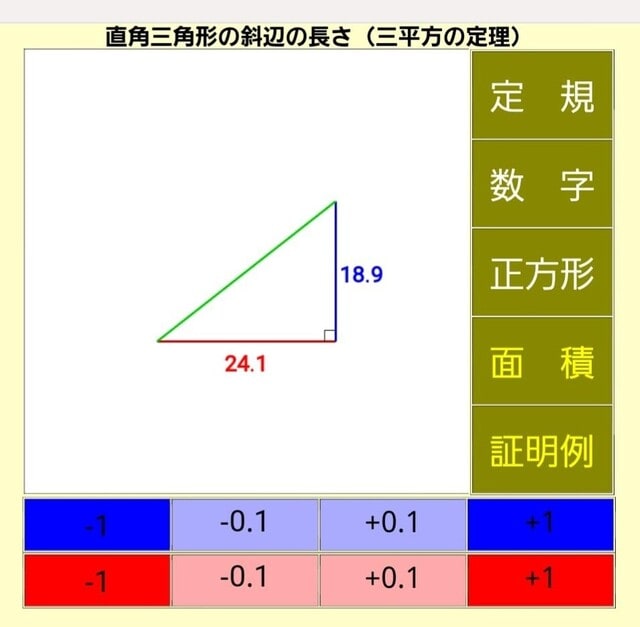
下のボタンで辺の長さを変えることができます。
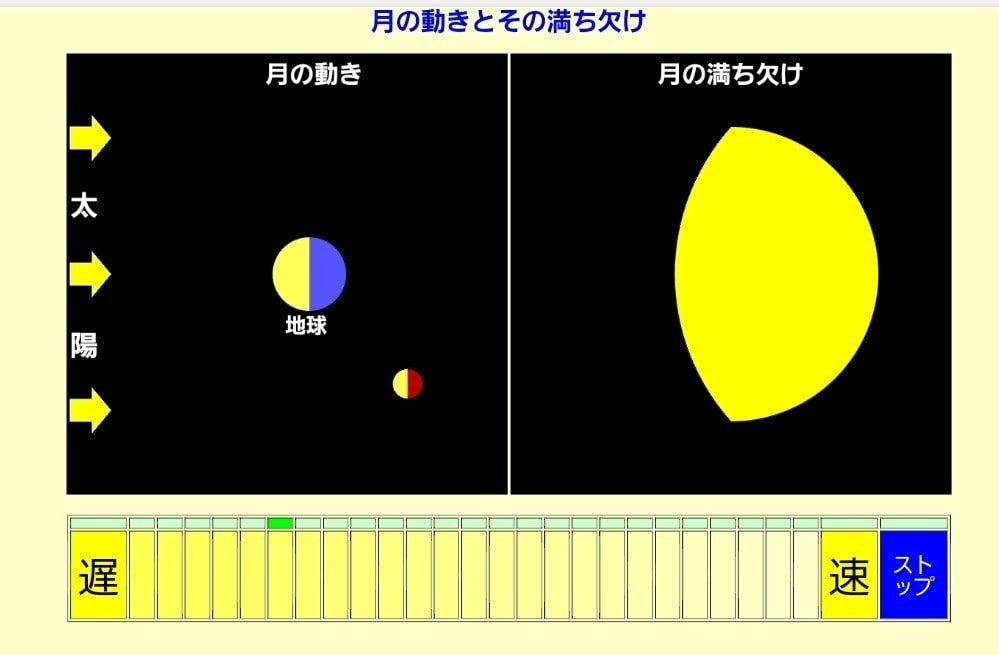
いくらかボタンを押して長さを変えたところです。
斜辺の長さを求めたいですね。
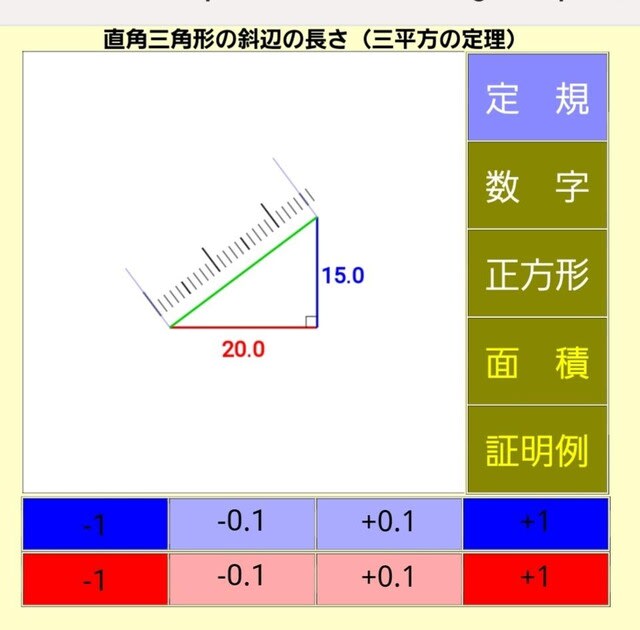
そこで、右側のボタン〈定規〉を押すと、
このように、斜辺にそって定規が表示されます。それを読むことで長さがわかります。
写真では、初期画面での定規表示になっていますが私のミスです。実際はその斜辺にそっての定規になります。スミマセン!
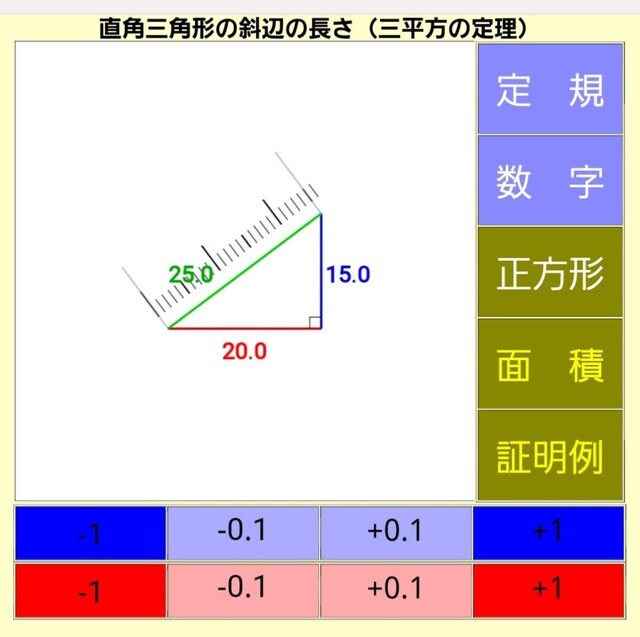
正しい測定値は〈定規〉の下の〈数字〉ボタンを押すと表示されます。
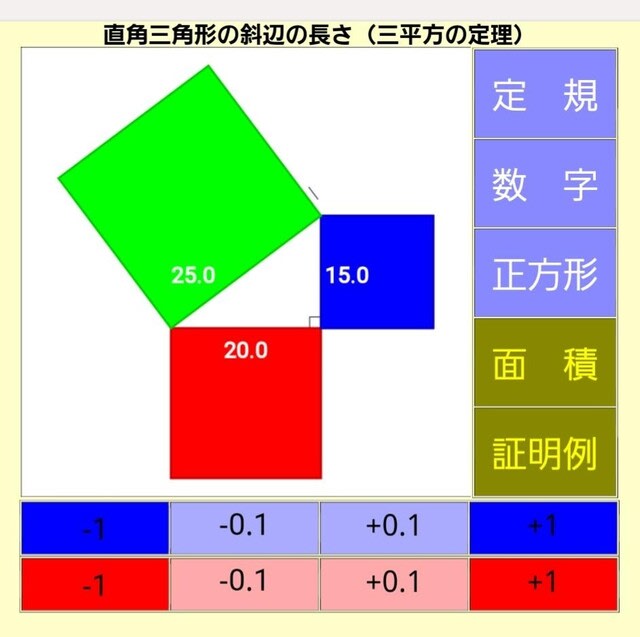
〈数字〉の下には〈正方形〉ボタンがあります。それを押すと、
それぞれの辺を一辺とした正方形が3つ表示されます。
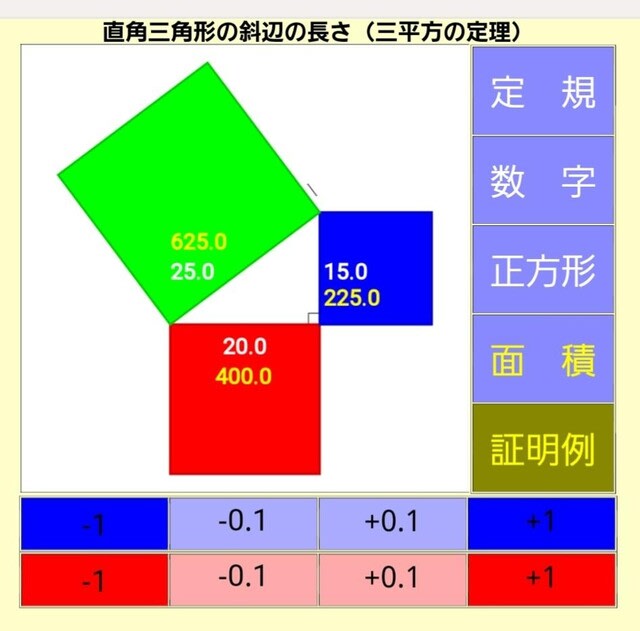
その下の〈面積〉ボタンを押すと、
黄色い数字で面積が表示されます。この場合は20、15、25という2乗しやすい数字ですが、小数点が付いたりする数字でも、瞬時に計算して表示してくれます。
この3つの正方形の面積の値から「三平方の定理」が成り立つこと「底辺の正方形の面積+縦辺の正方形の面積=斜辺の正方形の面積」を、実験的に”確認”することができます。底辺と縦辺の長さがどんなときも成り立つことがわかります。
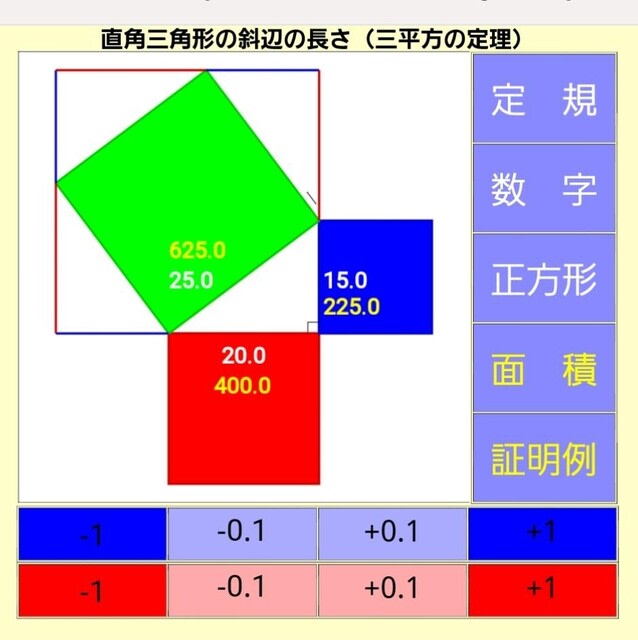
三平方の定理が図形的にも証明できるということを、次の〈証明例〉ボタンを押して、証明のヒントを表示します。
これです。同じ直角三角形を3つ描き加えることで、〔底辺の長さ+縦辺の長さ〕の辺を一辺とする正方形が描けます。この面積は計算できます。その正方形の中にある4つの直角三角形の面積も計算できます。このことから、前者から後者を引くと、斜辺を一辺とした正方形の面積となります。先ほどのabcでいうと、abからcが求まるということですから、
が証明されることになります。
〈証明例〉だけを押したときの画面です。
すっきりした表示になりました。この状態でも下のボタンを押して辺の長さを変えると図形が変化します。面白いです。
実際に使ってください。次のURLかバナー(図)を押すと、プログラムのある私のホームページに飛んで使うことができます。
この動く教材は ”使ってもらうこと” が一番の希望です。中学生や中学校や高校の数学の先生がおられましたら知らせてください。
スマホで使ってみたら、下のボタンが小さすぎますね。もうしばらくしたら修正してスマホ用を提供します。
追加 R07年02月12日 10時
スマホ用を作りました。 ボタンを大きくして、場所も下部にまとめました。










 タップで拡大図
タップで拡大図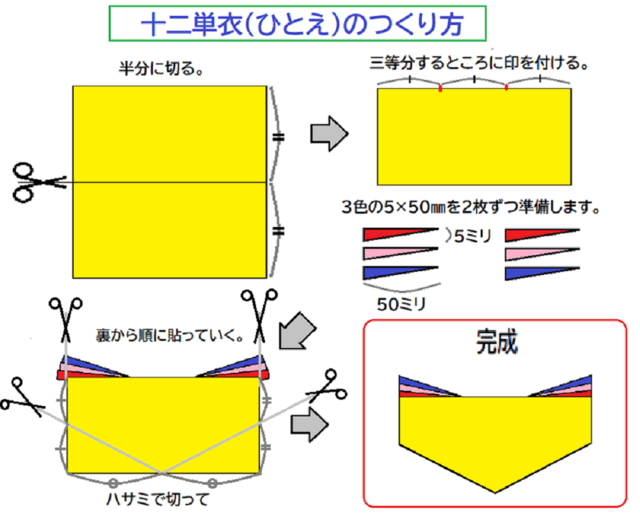
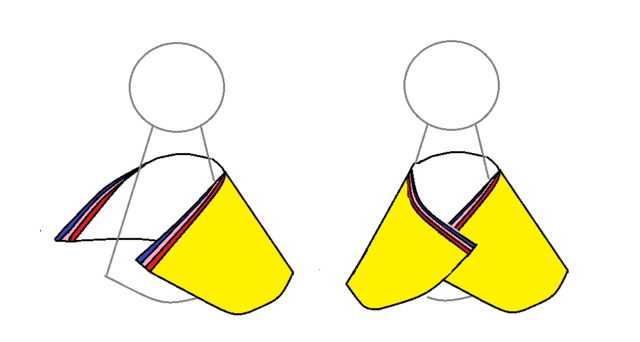
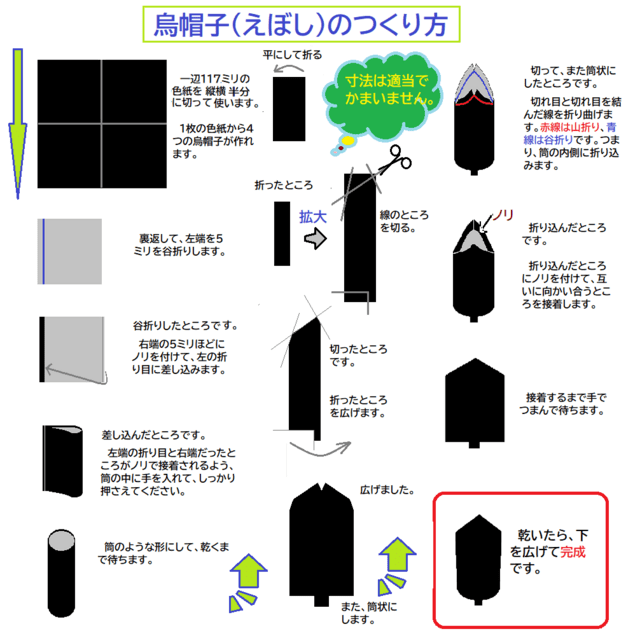
 タップで拡大
タップで拡大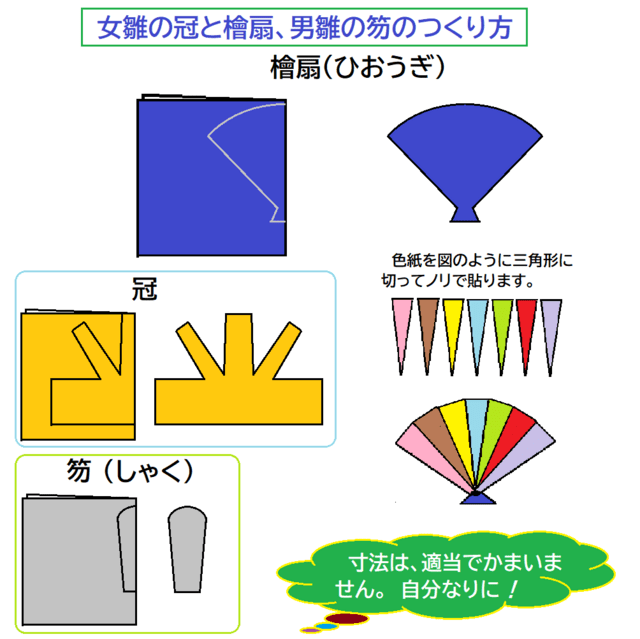
 タップで拡大
タップで拡大