今日も中学生向けの数学の話。メネラウスの定理のまとめだ。
先日は日本の高校受験参考書と睨めっこをしながら、下の様に(AC/CF)×(FE/EB)×(BD/DA)=1 を導いてみた。

DCと平行な線をFから引き、ABとの交点をPとする。
AC:CF=DA:DP
AC・DP=DA・CF
(AC/CF)=(DA/DP) ---①
FE:EB=DP:BD
FE・BD=DP・EB
(FE/EB)=(DP/BD) ---②
①×②
(AC/CF)×(FE/EB)=(DA/DP)×(DP/BD)
両辺へ(BD/DA)を掛ける。
(AC/CF)×(FE/EB)×(BD/DA)=(DA/DP)×(DP/BD)×(BD/DA)
(AC/CF)×(FE/EB)×(BD/DA)=1
辺AC上のACとCFの割合(AC/CF)を辺AB上のDAとDPの割合(DA/DP)へ変換し、辺FB上のFEとEBの割合(FE/EB)も辺AB上のDPとBDの割合(DP/BD)に変換。この2つの割合を掛け合せた上へ辺AB上のBDとDAの割合BD/DAも掛けると1になると導いているが、中1の娘は理解できてもスッキリでは無いらしく、タイヤイさんから頂いたアドバイスと問題集の模範解答を参考に「高さが等しい三角形は、面積比と底辺の長さの比が等しい」のを利用してメネラウスの定理を導いてみたい。
先ずはメネラウスの定理を導く基になる「高さが等しい三角形は、面積比と底辺の長さの比が等しい」の話から。

⊿ABGと⊿ACGは共に高さがhの三角形。
⊿ABGの面積S1=(BG×h)÷2
⊿ACGの面積S2=(CG×h)÷2
S1:S2=(BG×h)÷2:(CG×h)÷2
=BG:CG
⊿ABGの面積S1と⊿ACGの面積S2の面積比は、⊿ABGの底辺BGと⊿ACGの底辺CGの長さの比と等しい。

⊿EBGと⊿ECGは共に高さがjの三角形。
⊿EBGの面積S3=(BG×j)÷2
⊿ECGの面積S4=(CG×j)÷2
S3:S4=(BG×j)÷2:(CG×j)÷2
=BG:CG
⊿EBGの面積S3と⊿ECGの面積S4の面積比は、⊿EBGの底辺BGと⊿ECGの底辺CGの長さの比と等しい。
⊿ABEの面積S5=S1-S3
=((BG×h)÷2)-((BG×j)÷2)
=BG(h-j)÷2
⊿ACEの面積S6=S2-S4
=((CG×h)÷2)-((CG×j)÷2)
=CG(h-j)÷2
⊿ABEの面積S5:⊿ACEの面積S6=S1-S3:S2-S4
=BG(h-j)÷2:CG(h-j)÷2
=BG:CG
⊿ABEの面積S5と⊿ACEの面積S6の面積比は、BGとCGの長さの比と等しい。
ここまでを理解したらメネラウスの定理へ入ろう。
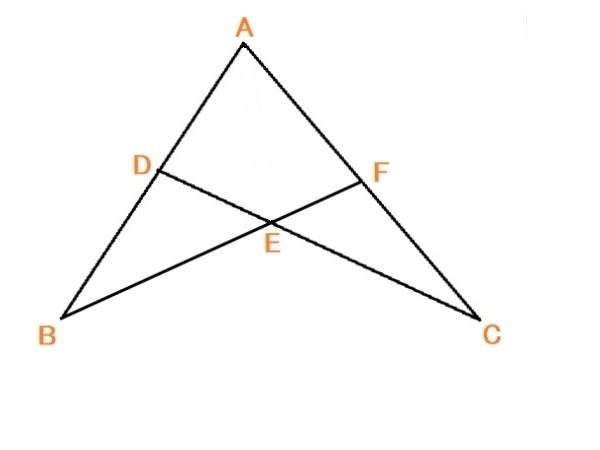
このままでは難しいので、以下の様にAEとBCへ補助線を入れ、⊿EAFの面積をS1 ⊿ECFの面積をS2 ⊿EBCの面積をS3とする。

⊿EAFと⊿ECFは高さが等しい三角形で、面積比S1:S2と底辺の長さの比AF:CFが等しいので、
AC/CF=(S1+S2)/S2
⊿ECFと⊿EBCは高さが等しい三角形で、面積比S2:S3と底辺の長さの比FE:EBが等しいので、
FE/EB=S2/S3
⊿EBCと⊿EACの面積比S3:(S1+S2)と 辺BDと辺DAの長さの比BD:DAが等しいので、
BD/DA=S3/(S1+S2)
(AC/CF)・(FE/EB)・(BD/DA)=((S1+S2)/S2)・(S2/S3)・(S3/(S1+S2))
=((S1+S2)/S2)・(S2/S3)・(S3/(S1+S2))
=1
「高さが等しい三角形は、面積比と底辺の長さの比が等しい」を利用するとメネラウスの定理を簡単に導ける。
同じ方法でチェバの定理も導く。
チェバの定理についての詳細な解説はウィキペディアを参照。 日本語のページ タイ語のページ

チェバの定理とは上の図で(AD/DB)・(BG/GC)・(CF/FA)=1の等式が成立する定理。
AD/DB=⊿ECA/⊿ECB=S2/S3
BG/GC=⊿EAB/⊿ECA=S1/S2
CF/FA=⊿ECB/⊿EAB=S3/S1 なので
(AD/DB)・(BG/GC)・(CF/FA)=(S2/S3)・(S1/S2)・(S3/S1)
=(S2/S3)・(S1/S2)・(S3/S1)
=1
このくらいに書くと中1の娘でも理解できるそうだ。単に式だけ覚えるより良いだろう。メネラウスの定理もチェバの定理も中学や高校では教えないらしく、タイの高校受験や大学受験の問題集でも「高さが等しい三角形は、面積比と底辺の長さの比が等しい」のを利用して解いてあるが、そんなことをやっていたのでは1問3分で解くのは難しい。この2つの定理は受験の時に強力な武器として働いてくれるだろう。
タイの中学生向け数学ギフテッド問題の記事へのリンク→#高1入試ギフ
タイの高校生向け数学入試問題の記事へのリンク→#大学入試
貴方のクリックとコメントが、このブログのパワーの源です。
下の2つのバナーへ応援クリックをお願いします。
 海外生活ブログ タイ情報 人気ランキングはこちら
海外生活ブログ タイ情報 人気ランキングはこちら
リアルタイムに更新される新着記事一覧(右下)からタイの今が見える。お薦め。
 タイの人気ブログが大集合!!
タイの人気ブログが大集合!!
登録数 アクセス数 最大級のブログランキング
ブログの世界が広がります。

先日は日本の高校受験参考書と睨めっこをしながら、下の様に(AC/CF)×(FE/EB)×(BD/DA)=1 を導いてみた。

DCと平行な線をFから引き、ABとの交点をPとする。
AC:CF=DA:DP
AC・DP=DA・CF
(AC/CF)=(DA/DP) ---①
FE:EB=DP:BD
FE・BD=DP・EB
(FE/EB)=(DP/BD) ---②
①×②
(AC/CF)×(FE/EB)=(DA/DP)×(DP/BD)
両辺へ(BD/DA)を掛ける。
(AC/CF)×(FE/EB)×(BD/DA)=(DA/DP)×(DP/BD)×(BD/DA)
(AC/CF)×(FE/EB)×(BD/DA)=1
辺AC上のACとCFの割合(AC/CF)を辺AB上のDAとDPの割合(DA/DP)へ変換し、辺FB上のFEとEBの割合(FE/EB)も辺AB上のDPとBDの割合(DP/BD)に変換。この2つの割合を掛け合せた上へ辺AB上のBDとDAの割合BD/DAも掛けると1になると導いているが、中1の娘は理解できてもスッキリでは無いらしく、タイヤイさんから頂いたアドバイスと問題集の模範解答を参考に「高さが等しい三角形は、面積比と底辺の長さの比が等しい」のを利用してメネラウスの定理を導いてみたい。
先ずはメネラウスの定理を導く基になる「高さが等しい三角形は、面積比と底辺の長さの比が等しい」の話から。

⊿ABGと⊿ACGは共に高さがhの三角形。
⊿ABGの面積S1=(BG×h)÷2
⊿ACGの面積S2=(CG×h)÷2
S1:S2=(BG×h)÷2:(CG×h)÷2
=BG:CG
⊿ABGの面積S1と⊿ACGの面積S2の面積比は、⊿ABGの底辺BGと⊿ACGの底辺CGの長さの比と等しい。

⊿EBGと⊿ECGは共に高さがjの三角形。
⊿EBGの面積S3=(BG×j)÷2
⊿ECGの面積S4=(CG×j)÷2
S3:S4=(BG×j)÷2:(CG×j)÷2
=BG:CG
⊿EBGの面積S3と⊿ECGの面積S4の面積比は、⊿EBGの底辺BGと⊿ECGの底辺CGの長さの比と等しい。
⊿ABEの面積S5=S1-S3
=((BG×h)÷2)-((BG×j)÷2)
=BG(h-j)÷2
⊿ACEの面積S6=S2-S4
=((CG×h)÷2)-((CG×j)÷2)
=CG(h-j)÷2
⊿ABEの面積S5:⊿ACEの面積S6=S1-S3:S2-S4
=BG(h-j)÷2:CG(h-j)÷2
=BG:CG
⊿ABEの面積S5と⊿ACEの面積S6の面積比は、BGとCGの長さの比と等しい。
ここまでを理解したらメネラウスの定理へ入ろう。

このままでは難しいので、以下の様にAEとBCへ補助線を入れ、⊿EAFの面積をS1 ⊿ECFの面積をS2 ⊿EBCの面積をS3とする。

⊿EAFと⊿ECFは高さが等しい三角形で、面積比S1:S2と底辺の長さの比AF:CFが等しいので、
AC/CF=(S1+S2)/S2
⊿ECFと⊿EBCは高さが等しい三角形で、面積比S2:S3と底辺の長さの比FE:EBが等しいので、
FE/EB=S2/S3
⊿EBCと⊿EACの面積比S3:(S1+S2)と 辺BDと辺DAの長さの比BD:DAが等しいので、
BD/DA=S3/(S1+S2)
(AC/CF)・(FE/EB)・(BD/DA)=((S1+S2)/S2)・(S2/S3)・(S3/(S1+S2))
=((
=1
「高さが等しい三角形は、面積比と底辺の長さの比が等しい」を利用するとメネラウスの定理を簡単に導ける。
同じ方法でチェバの定理も導く。
チェバの定理についての詳細な解説はウィキペディアを参照。 日本語のページ タイ語のページ

チェバの定理とは上の図で(AD/DB)・(BG/GC)・(CF/FA)=1の等式が成立する定理。
AD/DB=⊿ECA/⊿ECB=S2/S3
BG/GC=⊿EAB/⊿ECA=S1/S2
CF/FA=⊿ECB/⊿EAB=S3/S1 なので
(AD/DB)・(BG/GC)・(CF/FA)=(S2/S3)・(S1/S2)・(S3/S1)
=(
=1
このくらいに書くと中1の娘でも理解できるそうだ。単に式だけ覚えるより良いだろう。メネラウスの定理もチェバの定理も中学や高校では教えないらしく、タイの高校受験や大学受験の問題集でも「高さが等しい三角形は、面積比と底辺の長さの比が等しい」のを利用して解いてあるが、そんなことをやっていたのでは1問3分で解くのは難しい。この2つの定理は受験の時に強力な武器として働いてくれるだろう。
タイの中学生向け数学ギフテッド問題の記事へのリンク→#高1入試ギフ
タイの高校生向け数学入試問題の記事へのリンク→#大学入試
貴方のクリックとコメントが、このブログのパワーの源です。
下の2つのバナーへ応援クリックをお願いします。
 海外生活ブログ タイ情報 人気ランキングはこちら
海外生活ブログ タイ情報 人気ランキングはこちらリアルタイムに更新される新着記事一覧(右下)からタイの今が見える。お薦め。
 タイの人気ブログが大集合!!
タイの人気ブログが大集合!!登録数 アクセス数 最大級のブログランキング
ブログの世界が広がります。

















