FACEBOOKのローカルニュースページ「Udonthani skyline」で知ったのだが、2020年にウドンタニへ大手インター校が開校するらしい。
今までもウドンタニへインター校と称する学校はいくつか有っても、インター校と言いながら児童はタイ語しか話せなかったり、運営の実態が不明確だったりで、私は何となく不安を感じて見ていたのだが、ようやくある程度の規模のインター校が開校する様だ。
ウドンタニは国際結婚カップルが多い街で、娘が通ったキリスト教系の小学校ではクラスに数人は片親が外国人の児童だったが、自宅で父親の母語を話しているからか、それともタイの教育環境に慣れないのか、残念だがウドンタニでは「西洋人の子供は勉強ができない」と言われたりもする。
西洋式の充実した教育が行われば、そういう残念な評判は消えるだろう。
2020年にウドンタニへ開校を予定しているのは International Community School (ICS) で、バンコク校は1993年に開校し、約千人の児童・生徒が在籍しているそうだ。ウドンタニキャンパスのWEBページはこちら。ビデオも貼っておこう。
それでは前回の記事で出題した中学校で教えない因数分解の解答。
問1 ①~⑤を因数分解しなさい。
① (x+1)(x+2)(x+3)(x+4)+1
JIMMYさんから頂いた解答
(x+1)(x+2)(x+3)(x+4)+1
=x^4+10x^3+35x^2+50x+25
(x^2+〇+〇)でくくってみます。最後が25なので(x^2+〇+5)が見えてきます。
あとは〇に入るxを探せば(x^2+5x+5)になります。
x^4+10x^3+35x^2+50x+25を(x^2+5x+5)で割ったら、(x^2+5x+5)になりましたので(x^2+5x+5)^2となりました。
これ以上の分解では(x-(-5+√5)/2)^2*(x-(-5-√5)/2)^2ですが、そこまで分解しなくてもいいかと思います。
メンカームのコメント
◯=5は、後から見ればそうだなと思うのですが、自分で解く時に状況を調べて推理していく力が私には足りません。数学のセンスを付けなければなりません。
私、Menkarmの解答
最初に学校で教えられた通りに解いてみよう。
(x+1)(x+2)(x+3)(x+4)+1
=(x2+3x+2)(x2+7x+12)+1
=x4+ 7x3+12x2
+ 3x3+21x2+36x
+ 2x2+14x+24+1
=x4+10x3+35x2+50x+25
ここから因数分解したいが、上記の様にJIMMYさんは可能でも、私の能力ではこれ以上進めない。(恥w)
「係数を揃えて置き換える」因数分解。
(x+1)(x+2)(x+3)(x+4)の展開だが掛け合わせる順番を・・
(x+1)(x+4)(x+2)(x+3)と入れ替えると・・
(x+1)(x+2)(x+3)(x+4)+1
=(x+1)(x+4)(x+2)(x+3)+1
=(x2+5x+4)(x2+5x+6)+1 と、x2+5xまでの係数が揃った。
x2+5xをAと置き換えると
与式=(A+4)(A+6)+1
=A2+10A+25
=(A+5)2
Aを元のx2+5xに戻して
与式=(x2+5x+5)2
答え (x+1)(x+2)(x+3)(x+4)+1=(x2+5x+5)2
② x4+4
JIMMYさんから頂いた解答
x^4+4=0とおくと、x^4=-4、x^2=2iなので(x^2-2i)(x^2+2i)となりますが、複素数の因数分解でもいいのかな。
メンカームのコメント
設問の引用元にも指定は無かったので、複素数(i2=-1)を使った因数分解でも良いでしょう。
私は中学生な娘向きに、複素数を使わない因数分解をやりました。
私、Menkarmの解答
中学校では4乗はやらないし、例え2乗でもこのパターンの因数分解は教えないだろう。
「a2-b2を作る」因数分解
x2をAと置き換えると
x4+4=A2+4
(A+2)2=A2+4A+4なので
A2+4=(A+2)2-4A
Aを元のx2に戻して
(A+2)2-4A
=(x2+2)2-4x2
=(x2+2)2-(2x)2
a2-b2=(a+b)(a-b)なので
(x2+2)2-(2x)2
=(x2+2+2x)(x2+2-2x)
=(x2+2x+2)(x2-2x+2)
答え x4+4=(x2+2x+2)(x2-2x+2)
③ (x2-1)(y2-1)-4xy
私、Menkarmの解答
たすき掛け(クロス法)は数だけでは無く、文字係数でも出来る。
「文字係数もたすき掛けする」因数分解
(x2-1)(y2-1)-4xy
=x2y2-x2-y2-4xy+1
=(y2-1)x2-4yx-(y2-1)
=(y-1)(y+1)x2-4yx-(y-1)(y+1)
ここで文字係数の「たすき掛け(クロス法)」←たすき掛けをご存じない時はクリック。
y-1 -(y+1) -y2-2y-1
✕
y+1 (y-1) y2-2y+1 +
4y
与式=((y-1)x-(y+1))((y+1)x+(y-1))
=(xy-x-y-1)(xy+x+y-1)
答え (x2-1)(y2-1)-4xy=(xy-x-y-1)(xy+x+y-1)
④ 5x2-56x-1536
JIMMYさんから頂いた解答
1536を素数に分解すると1536=3×2×2×2×2×2×2×2×2×2
そこでクロス法を用いて(x-a)(5x+b)=0
5X^2=5×1*X^2
-a×b=-1536
とおいて5a+1b=-56
となればいいので、aとbは3×2×2×2と2×2×2×2×2×2のどちらかだろうと見当を付けます。結果はa=24,b=64
5x^2-56x-1536=(5x+64)(x-24)
メンカームのコメント
「aとbは3×2×2×2と2×2×2×2×2×2のどちらかだろうと見当を付け」られるのが羨ましい。私や娘はまだまだ経験不足です。
私、Menkarmの解答
たすき掛けで解けそうだが、適当な数が見つからない。こんな時は・・
「二次方程式の解の公式を使う」因数分解
仮に 5x2-56x-1536=0 として二次方程式の解の公式を利用してxを求める。
二次方程式の解の公式より ax2+bx+c=0の時のxの値は、
x=(-b±√b2-4ac)/(2a)なので、
x=(56±√562-4・5・(-1536))/(2・5)
=(56±√3136+30720)/10
=(56±√33856)/10
=(56±√26×232)/10 12~252まで要暗記。
=(56±23×23)/10
=(56±184)/10
=24 , -12.8
x=24は判るが、x=-12.8へピンと来ない私は因数定理を利用した組立除法を使って求める。
24| 5 -56 -1536
120 1536
5 64 0
(x-24)(5x+64)=0
答え 5x2-56x-1536=(x-24)(5x+64)
YOUTUBEへ簡単な因数分解の方法が有ったので貼っておく。
5x2-56x-1536
5 512=64×8 64 64
↓
1 3 8×-3=-24 -120
-56
これは簡単だ。
⑤ a3+3a2b+a2c+2ab2+2b2c+3abc (誤記修正しました。御指摘ありがとうございます。)
JIMMYさんから頂いた解答
(a+b)で割りますと、
(a+b)(a^2+2ab+ac+2bc)となるので、さらに因数分解して、
(a+b)(a+c)(a+2b)になりました。
メンカームのコメント
a+bで割れそうだなと、気が付かない私が悲しい。修行不足です。
私、Menkarmの解答
複雑で、どれを係数にするか悩んだ時は
「低い次数に着目した」因数分解
先ずは次数について。多項式の次数とは、その項が何乗であるか、または最高何乗の項を持つかを示す数を言う。
a3+3a2b+a2c+2ab2+2b2c+3abcは、aについて言えば最高3乗の項を持つので次数は3。bについては最高2乗の項を持つので次数は2。cは最高1乗の項なので次数は1となる。
与式を次数が3のaで整理すると
a3+3a2b+a2c+2ab2+2b2c+3abc
=a3+(3b+c)a2+(2b2+3bc)a+2b2c
残念だが、私の低い能力ではここから因数分解出来ない。
与式を次数が2のbで整理すると
a3+3a2b+a2c+2ab2+2b2c+3abc
=(2a+2c)b2+(3a2+3ac)b+a3+a2c
=(2a+2c)b2+(3a2+3ac)b+a(a2+ac)
2a+2c a2+ac a2+ ac
✕
1 a 2a2+2ac +
3a2+3ac
与式=((2a+2c)b+a2+ac)(b+a)
=(2(a+c)b+a(a+c))(b+a)
=(a+c)(2b+a)(b+a)
=(a+b)(a+2b)(a+c)
与式を次数が1のcで整理すると
a3+3a2b+a3c+2ab2+2b2c+3abc
=(a2+2b2+3ab)c+a3+3a2b+2ab2
=(a2+2b2+3ab)c+a(a2+3ab+2b2)
=(a+c)(a2+2b2+3ab)
=(a+b)(a+2b)(a+c)
多項式は次数が低い文字で整理し、次数が高い文字を係数とした方が、因数分解し易い場合があるのを理解出来ただろう。
問2 4x4-12x3+13x2-6x+1=(ax2+bx+c)2
a+b+c=?
JIMMYさんから頂いた解答
a=-2,b=3,c=-1になるのでa+b+c=0になりました。
今回も教えて下さったJIMMYさんへ感謝! m(_ _)m <いつも有難うございます。
私、Menkarmの解答
(ax2+bx+c)2
=(ax2+bx+c)(ax2+bx+c)
=a2x4+abx3+acx2
+abx3+ b2x2+bcx
+acx2+bcx+c2
=a2x4+2abx3+(b2+2ac)x2+2bcx+c2
4x4-12x3+13x2-6x+1と係数を比べると・・
a2=4、2ab=-12、b2+2ac=13、2bc=-6、c2=1
a2=4 より a=±2
a=2の時 2ab=-12より b=-3。
b2+2ac=13へ a=2 と b=-3 を代入して c=1
a=2、b=-3、c=1 で 2bc=-6 c2=1 となるのを確認。
a+b+c=0
a=-2の時 2ab=-12より b=3。
b2+2ac=13へ a=-2 と b=3 を代入して c=-1
a=-2、b=3、c=-1 で 2bc=-6 c2=1 となるのを確認。
a+b+c=0
答え a+b+c=0
いかがだっただろうか?JIMMYさんと私の解答を見て、私が感じる大きな違いは(当然能力の違いが大きいのだけど、それは置いといてw)「経験」の差。JIMMYさんは、多分この辺だなと推測されて、サクサクと解かれている。娘をそのレベルまで持って行きたいが、まだまだ時間が必要。
今回紹介した因数分解は高校レベルだが、このくらいを知らないと中学生向けでもレベルが高めの問題集に手が出せない。出来なくても中学校の成績には関係無いが、IJSO等の試験や高校で進学校の理数なんかを狙うと影響はあるだろう。
娘と私がやっている自宅での数学の学習で、学校で教えない定理や公式の学習を終えて、今はサマーコムカニッタサー試験の対策問題集に取り組んでおり、10月のピッタームで中2の範囲までを終わらせた。今回の記事で中1の1学期に自宅で学習して難しかった部分の紹介は終わり。
未だやるの?と言われそうだが、最後に息子の大学受験問題集から1問。
問
∠Aの角度を求めなさい。
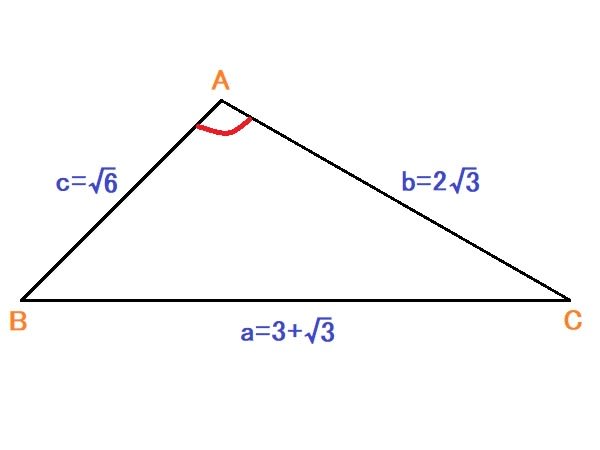
息子から教えてくれと頼まれて取り組んだが、中学生でも余裕で解ける問題だった。解答は1週間後に掲載。
タイの中学生向け数学ギフテッド問題の記事へのリンク→#高1入試ギフ
タイの高校生向け数学入試問題の記事へのリンク→#大学入試
貴方のクリックとコメントが、このブログのパワーの源です。
下の2つのバナーへ応援クリックをお願いします。
 海外生活ブログ タイ情報 人気ランキングはこちら
海外生活ブログ タイ情報 人気ランキングはこちら
リアルタイムに更新される新着記事一覧(右下)からタイの今が見える。お薦め。
 タイの人気ブログが大集合!!
タイの人気ブログが大集合!!
登録数 アクセス数 最大級のブログランキング
ブログの世界が広がります。

今までもウドンタニへインター校と称する学校はいくつか有っても、インター校と言いながら児童はタイ語しか話せなかったり、運営の実態が不明確だったりで、私は何となく不安を感じて見ていたのだが、ようやくある程度の規模のインター校が開校する様だ。
ウドンタニは国際結婚カップルが多い街で、娘が通ったキリスト教系の小学校ではクラスに数人は片親が外国人の児童だったが、自宅で父親の母語を話しているからか、それともタイの教育環境に慣れないのか、残念だがウドンタニでは「西洋人の子供は勉強ができない」と言われたりもする。
西洋式の充実した教育が行われば、そういう残念な評判は消えるだろう。
2020年にウドンタニへ開校を予定しているのは International Community School (ICS) で、バンコク校は1993年に開校し、約千人の児童・生徒が在籍しているそうだ。ウドンタニキャンパスのWEBページはこちら。ビデオも貼っておこう。
それでは前回の記事で出題した中学校で教えない因数分解の解答。
問1 ①~⑤を因数分解しなさい。
① (x+1)(x+2)(x+3)(x+4)+1
JIMMYさんから頂いた解答
(x+1)(x+2)(x+3)(x+4)+1
=x^4+10x^3+35x^2+50x+25
(x^2+〇+〇)でくくってみます。最後が25なので(x^2+〇+5)が見えてきます。
あとは〇に入るxを探せば(x^2+5x+5)になります。
x^4+10x^3+35x^2+50x+25を(x^2+5x+5)で割ったら、(x^2+5x+5)になりましたので(x^2+5x+5)^2となりました。
これ以上の分解では(x-(-5+√5)/2)^2*(x-(-5-√5)/2)^2ですが、そこまで分解しなくてもいいかと思います。
メンカームのコメント
◯=5は、後から見ればそうだなと思うのですが、自分で解く時に状況を調べて推理していく力が私には足りません。数学のセンスを付けなければなりません。
私、Menkarmの解答
最初に学校で教えられた通りに解いてみよう。
(x+1)(x+2)(x+3)(x+4)+1
=(x2+3x+2)(x2+7x+12)+1
=x4+ 7x3+12x2
+ 3x3+21x2+36x
+ 2x2+14x+24+1
=x4+10x3+35x2+50x+25
ここから因数分解したいが、上記の様にJIMMYさんは可能でも、私の能力ではこれ以上進めない。(恥w)
「係数を揃えて置き換える」因数分解。
(x+1)(x+2)(x+3)(x+4)の展開だが掛け合わせる順番を・・
(x+1)(x+4)(x+2)(x+3)と入れ替えると・・
(x+1)(x+2)(x+3)(x+4)+1
=(x+1)(x+4)(x+2)(x+3)+1
=(x2+5x+4)(x2+5x+6)+1 と、x2+5xまでの係数が揃った。
x2+5xをAと置き換えると
与式=(A+4)(A+6)+1
=A2+10A+25
=(A+5)2
Aを元のx2+5xに戻して
与式=(x2+5x+5)2
答え (x+1)(x+2)(x+3)(x+4)+1=(x2+5x+5)2
② x4+4
JIMMYさんから頂いた解答
x^4+4=0とおくと、x^4=-4、x^2=2iなので(x^2-2i)(x^2+2i)となりますが、複素数の因数分解でもいいのかな。
メンカームのコメント
設問の引用元にも指定は無かったので、複素数(i2=-1)を使った因数分解でも良いでしょう。
私は中学生な娘向きに、複素数を使わない因数分解をやりました。
私、Menkarmの解答
中学校では4乗はやらないし、例え2乗でもこのパターンの因数分解は教えないだろう。
「a2-b2を作る」因数分解
x2をAと置き換えると
x4+4=A2+4
(A+2)2=A2+4A+4なので
A2+4=(A+2)2-4A
Aを元のx2に戻して
(A+2)2-4A
=(x2+2)2-4x2
=(x2+2)2-(2x)2
a2-b2=(a+b)(a-b)なので
(x2+2)2-(2x)2
=(x2+2+2x)(x2+2-2x)
=(x2+2x+2)(x2-2x+2)
答え x4+4=(x2+2x+2)(x2-2x+2)
③ (x2-1)(y2-1)-4xy
私、Menkarmの解答
たすき掛け(クロス法)は数だけでは無く、文字係数でも出来る。
「文字係数もたすき掛けする」因数分解
(x2-1)(y2-1)-4xy
=x2y2-x2-y2-4xy+1
=(y2-1)x2-4yx-(y2-1)
=(y-1)(y+1)x2-4yx-(y-1)(y+1)
ここで文字係数の「たすき掛け(クロス法)」←たすき掛けをご存じない時はクリック。
y-1 -(y+1) -y2-2y-1
✕
y+1 (y-1) y2-2y+1 +
4y
与式=((y-1)x-(y+1))((y+1)x+(y-1))
=(xy-x-y-1)(xy+x+y-1)
答え (x2-1)(y2-1)-4xy=(xy-x-y-1)(xy+x+y-1)
④ 5x2-56x-1536
JIMMYさんから頂いた解答
1536を素数に分解すると1536=3×2×2×2×2×2×2×2×2×2
そこでクロス法を用いて(x-a)(5x+b)=0
5X^2=5×1*X^2
-a×b=-1536
とおいて5a+1b=-56
となればいいので、aとbは3×2×2×2と2×2×2×2×2×2のどちらかだろうと見当を付けます。結果はa=24,b=64
5x^2-56x-1536=(5x+64)(x-24)
メンカームのコメント
「aとbは3×2×2×2と2×2×2×2×2×2のどちらかだろうと見当を付け」られるのが羨ましい。私や娘はまだまだ経験不足です。
私、Menkarmの解答
たすき掛けで解けそうだが、適当な数が見つからない。こんな時は・・
「二次方程式の解の公式を使う」因数分解
仮に 5x2-56x-1536=0 として二次方程式の解の公式を利用してxを求める。
二次方程式の解の公式より ax2+bx+c=0の時のxの値は、
x=(-b±√b2-4ac)/(2a)なので、
x=(56±√562-4・5・(-1536))/(2・5)
=(56±√3136+30720)/10
=(56±√33856)/10
=(56±√26×232)/10 12~252まで要暗記。
=(56±23×23)/10
=(56±184)/10
=24 , -12.8
x=24は判るが、x=-12.8へピンと来ない私は因数定理を利用した組立除法を使って求める。
24| 5 -56 -1536
120 1536
5 64 0
(x-24)(5x+64)=0
答え 5x2-56x-1536=(x-24)(5x+64)
YOUTUBEへ簡単な因数分解の方法が有ったので貼っておく。
5x2-56x-1536
5 512=64×8 64 64
↓
1 3 8×-3=-24 -120
-56
これは簡単だ。
⑤ a3+3a2b+a2c+2ab2+2b2c+3abc (誤記修正しました。御指摘ありがとうございます。)
JIMMYさんから頂いた解答
(a+b)で割りますと、
(a+b)(a^2+2ab+ac+2bc)となるので、さらに因数分解して、
(a+b)(a+c)(a+2b)になりました。
メンカームのコメント
a+bで割れそうだなと、気が付かない私が悲しい。修行不足です。
私、Menkarmの解答
複雑で、どれを係数にするか悩んだ時は
「低い次数に着目した」因数分解
先ずは次数について。多項式の次数とは、その項が何乗であるか、または最高何乗の項を持つかを示す数を言う。
a3+3a2b+a2c+2ab2+2b2c+3abcは、aについて言えば最高3乗の項を持つので次数は3。bについては最高2乗の項を持つので次数は2。cは最高1乗の項なので次数は1となる。
与式を次数が3のaで整理すると
a3+3a2b+a2c+2ab2+2b2c+3abc
=a3+(3b+c)a2+(2b2+3bc)a+2b2c
残念だが、私の低い能力ではここから因数分解出来ない。
与式を次数が2のbで整理すると
a3+3a2b+a2c+2ab2+2b2c+3abc
=(2a+2c)b2+(3a2+3ac)b+a3+a2c
=(2a+2c)b2+(3a2+3ac)b+a(a2+ac)
2a+2c a2+ac a2+ ac
✕
1 a 2a2+2ac +
3a2+3ac
与式=((2a+2c)b+a2+ac)(b+a)
=(2(a+c)b+a(a+c))(b+a)
=(a+c)(2b+a)(b+a)
=(a+b)(a+2b)(a+c)
与式を次数が1のcで整理すると
a3+3a2b+a3c+2ab2+2b2c+3abc
=(a2+2b2+3ab)c+a3+3a2b+2ab2
=(a2+2b2+3ab)c+a(a2+3ab+2b2)
=(a+c)(a2+2b2+3ab)
=(a+b)(a+2b)(a+c)
多項式は次数が低い文字で整理し、次数が高い文字を係数とした方が、因数分解し易い場合があるのを理解出来ただろう。
問2 4x4-12x3+13x2-6x+1=(ax2+bx+c)2
a+b+c=?
JIMMYさんから頂いた解答
a=-2,b=3,c=-1になるのでa+b+c=0になりました。
今回も教えて下さったJIMMYさんへ感謝! m(_ _)m <いつも有難うございます。
私、Menkarmの解答
(ax2+bx+c)2
=(ax2+bx+c)(ax2+bx+c)
=a2x4+abx3+acx2
+abx3+ b2x2+bcx
+acx2+bcx+c2
=a2x4+2abx3+(b2+2ac)x2+2bcx+c2
4x4-12x3+13x2-6x+1と係数を比べると・・
a2=4、2ab=-12、b2+2ac=13、2bc=-6、c2=1
a2=4 より a=±2
a=2の時 2ab=-12より b=-3。
b2+2ac=13へ a=2 と b=-3 を代入して c=1
a=2、b=-3、c=1 で 2bc=-6 c2=1 となるのを確認。
a+b+c=0
a=-2の時 2ab=-12より b=3。
b2+2ac=13へ a=-2 と b=3 を代入して c=-1
a=-2、b=3、c=-1 で 2bc=-6 c2=1 となるのを確認。
a+b+c=0
答え a+b+c=0
いかがだっただろうか?JIMMYさんと私の解答を見て、私が感じる大きな違いは(当然能力の違いが大きいのだけど、それは置いといてw)「経験」の差。JIMMYさんは、多分この辺だなと推測されて、サクサクと解かれている。娘をそのレベルまで持って行きたいが、まだまだ時間が必要。
今回紹介した因数分解は高校レベルだが、このくらいを知らないと中学生向けでもレベルが高めの問題集に手が出せない。出来なくても中学校の成績には関係無いが、IJSO等の試験や高校で進学校の理数なんかを狙うと影響はあるだろう。
娘と私がやっている自宅での数学の学習で、学校で教えない定理や公式の学習を終えて、今はサマーコムカニッタサー試験の対策問題集に取り組んでおり、10月のピッタームで中2の範囲までを終わらせた。今回の記事で中1の1学期に自宅で学習して難しかった部分の紹介は終わり。
未だやるの?と言われそうだが、最後に息子の大学受験問題集から1問。
問
∠Aの角度を求めなさい。

息子から教えてくれと頼まれて取り組んだが、中学生でも余裕で解ける問題だった。解答は1週間後に掲載。
タイの中学生向け数学ギフテッド問題の記事へのリンク→#高1入試ギフ
タイの高校生向け数学入試問題の記事へのリンク→#大学入試
貴方のクリックとコメントが、このブログのパワーの源です。
下の2つのバナーへ応援クリックをお願いします。
 海外生活ブログ タイ情報 人気ランキングはこちら
海外生活ブログ タイ情報 人気ランキングはこちらリアルタイムに更新される新着記事一覧(右下)からタイの今が見える。お薦め。
 タイの人気ブログが大集合!!
タイの人気ブログが大集合!!登録数 アクセス数 最大級のブログランキング
ブログの世界が広がります。

















