タイでヒモ暮らしな私の家庭内の役割は子育てが主な事もあって、ネットでも教育関連の記事を興味を持って読むが、日経ビジネスのオンラインゼミナール「僕らの子育て」へ「AI時代、子育てで最強の「習い事」は何だ？」という記事があり、私がピンと来た部分を引用したので、先ずは読んで欲しい。AI時代、子育てで最強の「習い事」は何だ？子どもの習い事を決める時に、大切にすること。それは、その習い事を子どもが楽しいと思うかどうかです。楽しいと思わないと続きません。
僕は今は大学生になった娘が小さい頃、ゴルフを習わせようと思いました。普通、ゴルフスクールというと、練習場に行って、ルールを覚えて、一生懸命打って……という流れで日本では教えるのではないでしょうか。
けれど米国で同じように教えようとすると、「練習させてうまくさせることは親の仕事ではないですよ」と怒られたんです。子どもにそんなことをしても、ゴルフを嫌いになるだけだから、と。それよりも、ゴルフ場を走らせたり、バンカーの砂場でお城を作らせたり、ボールを手で投げさせたり。まずは「ゴルフ場＝楽しい場所」という経験をさせましょう、ということでした。
サッカーでも水泳でも一緒で、勝つために頑張るというのは、好きになればやるようになるのだと思います。大切なのは、どうやって子どもにそれを好きにさせるか。言い換えれば、いかに「課外活動＝楽しい、好き」という脳の条件反射をつくるのか。それが親の腕の見せどころだと思います。
お小遣いなどの報酬を与えるのが効く子もいれば、親が一緒に楽しむことが効く子もいるはずです。僕の場合は、そのスポーツを一緒に見に行って、「プロの試合はすごいね」と言ってみたり、テレビで試合を一緒に見たりしながら、「この選手、すごいよね」というコミュニケーションを自然につくっています。
記事では「習い事」について話して居られるが、そのまま「習い事」を「勉強」へ入れ替えても同じだろう。
私は勉強嫌いで、学校の授業は退屈なのでずっと寝ていたが、科学には興味があり、図書館へ行ってはそういう分野の本をよく読んだ。科学が好きになった切っ掛けは、幼稚園の年長組の時に母が作って見せてくれた車のプラモデル。電池とモーターで走行可能であり、しばらく遊んだ後にモーターを分解して中を引き出した記憶がある。それからタミヤの楽しい工作シリーズのパーツを使って車を作ったりして楽しみ、小学の高学年になると電子工作。中学生でアマチュア無線、パソコン・・・と興味の対象が少しずつ変化し、大人になってそういう分野が仕事になると、自然や生き物が面白くなった。
娘の勉強も、最初は１４という数の意味が理解できないところから始めたが、コインを使ってクイズ形式で遊びながら教え、そこから問題集を活用した学習も始め、頑張ったらご褒美付きで「全問正解セブン旅行」と自転車でセブンへ買い物へ行ったりと、甘く甘くやって一緒に遊んでいた。私も楽しんでいたが、あの頃の勉強は遊んでいるみたいで、勉強している気がしなかったと娘も言っている。
中学生になった今は昔のように遊びながらは勉強しないが、それでも娘は勉強が好きで面白いらしい。「勉強＝楽しい、好き」という脳の条件反射が出来上がっているのかも？
いま大学生な息子が小さい時は、好きな玩具を買い与え、家中をプラレールが走り回ったり、市販のラジコンを改造して公園で走らせたりとよく遊んだが、勉強は全部学校任せ。タイへ来てからは小学校のランクアップ転校に良い成績が必須ということもあって私が教えたが、小３くらいだと遊びながら教えるなんてやらないので、何度も同じ場所を間違えると叱ったりで、決して楽しくなかっただろう。
この影響は後々まで続き、大学受験で数学の成績が悪いので教えようとしても逃げ回って拒否。「私との勉強＝楽しくない、嫌い」という脳の条件反射が出来上がっていたのだろう。大手塾の模試が最悪で落ち込んでいる時に、問題を解いて見せてようやく受け入れて貰ったが、高３になって教えても、小学校から積み上げた物が教科書レベルしかないのが悲しかった。
親や祖父母等の親族が教えるのは、親側には大きな期待があり、子供側には遠慮が不要な甘えもあって、「教師でも我が子へ教えるのは難しい」という話もあるくらい。引用した記事を見ても小さい時が大切で、勉強や習い事を「楽しい・好き」と印象付け出来ないなら、「楽しくない・嫌い」となるより、関与しない方が良いのかも知れない。
ウドンタニで人気のいくつかの塾でも、お菓子やお小遣いを準備してゲーム形式で競わせるように教えている。ゲームへ積極的に参加する子は驚くほど早く伸びるが、無関心な子はさっぱり無駄になるので、入塾の申し込み時に目を見て話せなかったり、落ち着きがない子は排除される所もある。
娘が通っている英語塾は高校生以上向けのコースへ入れて頂いているが、やはり知っている単語を競わせたりで、毎回ゲームが有るそうだ。娘のライバルはＤ校のおかまちゃん。ずっとクラスで２位が続いていたが、先日やっと優勝だと言うので、何で競ったか尋ねると国の英語名。学校の地理の授業でアフリカの国を全部覚えるのをやったばかりだったそうで、アフリカの国名を連発して勝ち抜いたそうだ。子供向けコースではないので、景品も賞金も貰えないが、ゲームとなると燃えるらしい。これも条件反射が脳へ組み込まれているのかも？ｗ
さて、数学へ入ろう。
前回の問題
直線ＡＢと直線ＣＤの交点をＭとすると、３ＡＭ＝４ＭＢ ３ＣＭ＝ＭＤ となり、
直線ＡＢの長さは１４、∠ＡＢＤと∠ＡＣＤの角度が等しい時のＣＭの長さを求めなさい。
第３回ＩＪＳＯの一次試験問題より引用
直線ＡＢと直線ＣＤの交点をＭとすると、３ＡＭ＝４ＭＢ ３ＣＭ＝ＭＤ となり、
直線ＡＢの長さは１４、∠ＡＢＤと∠ＡＣＤの角度が等しい時のＣＭの長さを求めなさい。
第３回ＩＪＳＯの一次試験問題より引用
教科書的に真っ直ぐ解いた解答
教科書的に２つ三角形の相似を利用して解いてみる。（塾技数学１００ 塾技５６）
先ずは設問から図を書くと・・・
こんな風に書けるだろう。
設問より∠ＡＢＤ＝∠ＡＣＤであり、対頂角なので∠ＡＭＣ＝∠ＤＭＢ。
三角形の２つの角が等しいので、⊿ＭＡＣ∽⊿ＭＤＢ。（相似）
判り易く２つの三角形を並べて書いてみる。
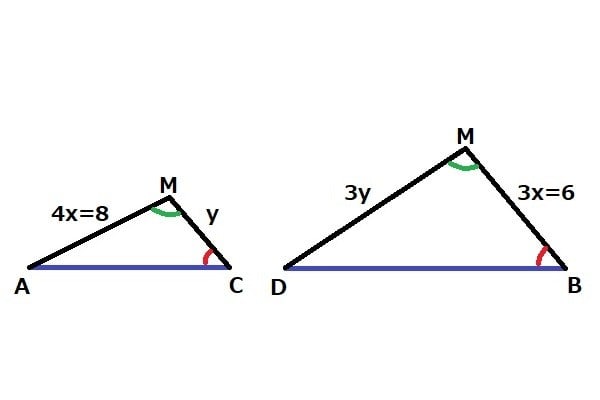
ＭＡ：ＭＤ＝ＭＣ：ＭＢ
８：３ｙ＝ ｙ：６
３ｙ2＝４８
ｙ2＝１６
ｙ＝４
ＣＭ＝ｙ＝４
答え ４
#相似 #辺の比 #中学数学
面積比を利用した解答
日本の中学受験参考書「塾技算数１００」で紹介されている「１組の角が等しい三角形の面積比は、その角を挟む２辺の長さの積の比と等しい（塾技６７）」を利用して解く。
先ずは設問から図を書くと・・・
こんな風に書けるだろう。
設問より∠ＡＢＤ＝∠ＡＣＤであり、対頂角なので∠ＡＭＣ＝∠ＤＭＢ。
三角形の２つの角が等しいので、⊿ＭＡＣ∽⊿ＭＤＢ。（相似）
判り易く２つの三角形を並べて書いてみる。
⊿ＭＡＣと⊿ＭＤＢの面積比は、等しい角を挟む２辺の長さの積の比と等しいので、
⊿ＭＡＣ：⊿ＭＤＢ＝４ｘ・ｙ：３ｘ・３ｙ＝４ｘｙ：９ｘｙ＝４：９
面積比が４：９の相似な図形の辺の長さの比は、√４：√９＝２：３。
ＣＭ＝（２／３）ＢＭ＝（２／３）・６＝４
答え ４
#辺の比 #面積比 #中学数学
方べきの定理を利用した解答
日本の高校受験参考書「塾技数学１００」で紹介されている「円と円周上に無い点があり、円周上に無い点を通る２直線と円周が交わる時、円周上に無い点と円周上の２点までの距離の積を方べきと言い、方べきの値は一定となる。（塾技６６）」を利用して解く。
先ずは設問から図を書くと・・・
となり、設問より∠ＡＢＤ＝∠ＡＣＤなので、「一つの弧に対する円周角の大きさは一定」という円周角の定理（塾技数学１００ 塾技６３）よりＡ・Ｂ・Ｃ・Ｄは同一円周上にあるのが判る。
方べきの定理より ＡＭ・ＢＭ＝ＣＭ・ＤＭ なので、
８・６＝ｙ・３ｙ
４８＝３ｙ2
ｙ2＝１６
ｙ＝４
ＣＭ＝ｙ＝４
答え ４
#方べきの定理 #中学数学
日本とタイでは出題傾向が異なるので全部はカバー出来ないが、タイで高校受験までの図形の勉強をさせるなら、日本の中学受験参考書「塾技算数１００」と高校入試参考書の「塾技数学１００」は、お薦めの参考書だ。タイの参考書へ書かれているのは教科書的な解法が多く、日本の至れり尽くせりで痒い所へ手が届きまくりな参考書を使えるのは日本語が読める人の特権（ｗ）と言っても良いだろう。
次の１問
半径６の内接円を持つ台形の、上底の長さが７で下底の長さが２１の時に、脚（縦長の２つの辺）の長さの差を求めなさい。
半径６の内接円を持つ台形の、上底の長さが７で下底の長さが２１の時に、脚（縦長の２つの辺）の長さの差を求めなさい。
設問へ図は無いが、解り難いので図を入れると下のようになる。
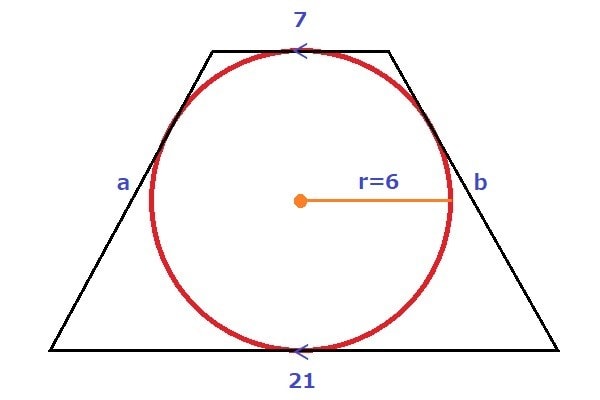
脚をそれぞれａとｂとした時に｜ａ－ｂ｜が求める答えとなる。
ムガさんのとこのお兄ちゃんに２問連続で簡単に答えられたので、今回は少し難しい問題にした。ｗ
タイの中学生向け数学ギフテッド問題の記事へのリンク→#高１入試ギフ
貴方のクリックとコメントが、このブログのパワーの源です。
下の２つのバナーへ応援クリックをお願いします。
海外生活ブログ タイ情報 人気ランキングはこちらリアルタイムに更新される新着記事一覧（右下）からタイの今が見える。お薦め。
タイの人気ブログが大集合！！登録数 アクセス数 最大級のブログランキング
ブログの世界が広がります。
