520万人の人々が雇用されているときには、乗数は50とたいそう大きいが、投資は当期所得のごくわずかな割合、すなわち0.06パーセントにすぎない。 (岩波文庫版 上 173-174)
本稿の目的は、この0.06%はどうやって計算したのか?である。
直接の計算式は「一般理論」本編中にはない。
一般理論の直前の記述から 0.06%の計算をしてみよう。
ケインズは詳細なノートを作っていたはずである。それは本編には載らなかった。載ったのは結論だけである。いわばここからはケインズの研究ノートを復元しようという試みである。
だから、原著を丁寧にノートを取りながら読んでいけば必ず理解できるのである。
第5節について、以下のように書き直してみる。以下は買って読んでからでないと・・・・見てはいけない。
もっとも単純な前提を導入する
- 500万人の雇用が生み出す所得をYとする。1人当たりが産み出す所得をXとする。
- Y=X×Nという一次関数の関係が短期では成り立つ。Nは雇用量。
- このとき消費性向は1とする。つまり生産したものは100%消費されるということである。
- 追加雇用10万人の追加生産物はその99%が消費される。以下10万人の追加雇用ごとに消費性向は1%ずつ下がっていくとする。仮定で重要なのはこの限界消費性向低下だけである。
この0.06%とは
520万人の人々が雇用されているときには、乗数は50とたいそう大きいが、投資は当期所得のごくわずかな割合、すなわち0.06パーセントにすぎない。
この文脈で想定されているのは、追加雇用と所得上昇は一次関数の関係を持つ、つまり⊿所得=Ⅹ×⊿雇用という関係を持つということである。1人当たりが産み出す所得をXとしたからである。なぜそうなるのかは前回検討した。検討外の要因は一定としておくということだ。
雇用500万人の場合
ここでは単純化のためにⅩ=1 かつ 500 万人の雇用が生み出す所得を500 とする。単位はどうでもよい。このとき、先ほどの前提から総消費は500、総投資は0 である。

追加雇用10に対する所得増加は10。所得増加に対する限界消費性向は前提4から1ポイント下がって0.99となるから消費額は9.9増えるという意味。このとき均衡条件の下では投資は10-9.9で0.1増えているはず。
次の追加雇用10に対しても所得増加は10。限界消費性向はさらに下がって0.98となる。投資は2%だから、投資乗数はその逆数50となる。

このときの総消費は500+9.9+9.8、総投資は0+0.1+0.2である。
上記から投資は当期所得の(0.1+0.2)÷500=0.06%増えたということになる。が、ケインズは喩えとして使っており数式に意味はない。
??という人は、総所得=総消費+総投資 を思い出すように。均衡条件下の仮定である。そのとき完全雇用が達成されているとは限らない。一般理論の一貫した前提である。
投資額0.3(0.1+0.2)から0.1へと三分の二に減少したとしても雇用は520万人から510万人へ10万人(1.92%)減るに過ぎない。
先ほどの仮定を過去の統計からもっと精緻で複雑なものにすることはいくらでも可能だが、ここは限界消費性向低下の法則という仮定が合っているかどうかの検証だけである。また複雑・精緻にしたところで現実にそれだけ迫れるというものでもないだろう。
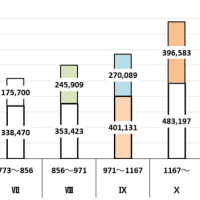
一方、雇用が900万人の時はどうだろう

*消費性向は追加雇用10万人あたり1%ずつ下がる。
*総消費=当期総消費500+Σ⊿消費、総投資は0+Σ⊿投資となる
総雇用900万人のときの総消費は818、総投資は82。総所得は900である。
投資が三分の一になったら、総投資は19となり、総投資が19のときの雇用は690万人と23.3%減ることになる。このとき総消費は671、総所得は690である。
すなわち、
乗数は貧しい社会のほうが大きいのに対し、投資変動の雇用に及ぼす影響は、もし当期産出量に占める当期投資の割合が富裕な社会のほうがずっと大きいものとすれば、富裕な社会のほうがはるかに大きくなるだろう。
というわけである。考えてみれば我々の経験にも合致する。「豊かな社会」ほど所得は投資に依存する。なぜなら消費性向が低いからである。投資の変動による雇用の変動も大きくなる。これこそ我々が、ずーっと、ずーっと体験してきたことである。
またこのとき、完全雇用に近づくほど、その達成は困難になるということでもある。投資乗数は投資割合の逆数となるので、限界消費性向低下法則の下では投資乗数が逓減するからである。雇用量520万人のときは50であるのに雇用量900万人のときは2.5まで低下する。多少の投資では雇用量を維持するのは難しいのである。
豊かになるほど完全雇用達成は難しい
ここからケインズが導き出す結論は、投資(公共投資)の影響は深刻な不況のとき、非自発的失業が大量に存在しているときは、投資が雇用に及ぼす影響は大きい(失業対策として効果的)ということである。
使われない貯蓄は、何かに使ってしまったほうがいい。利益を生むかどうか、という問題、回収とか金利とかの問題ではないのだ。投資は必ず総所得を増やすから。
このあと、有名な、しかも最も誤解されている「穴を掘って埋める」という喩えが出てくる。
このような表から数理経済学的な方程式や結論を導き出そうとしてもムダ。経済のコントロールは押したり引いたりして経過を見ながらやっていくしかない。
ケインズは数学が得意であったそうだ。数学や統計学はケインズの時代から何ほどの進歩があったわけでもない。進歩したのは道具である。複雑な数式を一瞬で解ける道具ができただけである。しかし解けるからと言ってそれが正解とは限らないのだ。現実離れした前提(絶対均衡条件)から出発すれば・・・永遠に正解は得られない。
ケインズの経済学での数学の利用についての考え方は後で出てくる。
限界消費性向の低下を補うだけの投資が増える
という保証は全くないのである
それどころか
「豊かな社会」ほど完全雇用達成のためには
より多くを投資に頼らざるをえないのである
公共投資害悪論を振りまく人々は、
自由放任の下でも「限界消費性向の低下を補うだけの投資が増える」
という命題を証明していただきたい。