スパイクの角度とボール落下点の不思議な関係（誤解しているとレシーバーはポジション取りを間違います。）

にほんブログ村
問題
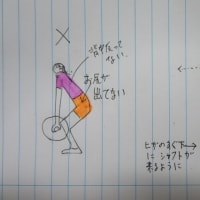
　問題は、上記の図のとおり、アタッカーが最短飛距離４．４ｍの●から最長飛距離１０．４ｍの●までの間にスパイクする許容範囲（●から●まで７．４ｍ）を持っている場合に、下図のとおり、上下のスパイクの許容角度のちょうど真ん中になる方向にスパイクを打つと、ボールは、どの辺に落ちるか？
というものでした。

解答
　一番足長にスパイクした場合の飛距離１０．４ｍのスパイクボール落下点●の位置よりも
５．２ｍ手前に落ちる。
が正解です。

考え方
「三角形の二等分線に関する公式」って、あったでしょう？ボールの自然落下する分を無視してスパイクボールを直線の運動として考えると、下の式のとおりとなり、上記の解答が導けます。
　　　　　　　　　　　　
で、この公式を今回のスパイクに当てはめると下図のようになります。

スパイクする瞬間のボールの位置●三角形の頂点Ａ
最も飛距離が短くなる場合のボールの位置●をＢ
最も、足長にスパイクされた場合のボールの位置●をＣ
としますね。
アタッカーは、リスクの少ない●Ｂと●Ｃの中間の角度にスパイクを打つとですね、スパイクの落ちる場所は●Ｄとなり、●Ｂと●Ｃの間の前方３分の１以下のかなり手前に落とされるってことになるのですね。
　　　　　　　　　　　　
勘違いするパターン　
　中学生に出題するとですね、勘違いするパターンは
　　　「７．４ｍ÷２＝３．７ｍ」
っていうのが多いです。
　
　ときどきひと癖持ってる男子が私の性格を読み「３．７ｍ以外！」とか「逆回転になって伸びるから、後ろから２ｍ。」などと言うのがいたりしますが、こういう連中は人の性格や他の要素を読もうとする点でセッターに使えるかも・・・・って考えたりしますね。
　
　中には、とにかく数字を触って「１０．４－４．４＝６ｍ」って答え導いて来て、正解に近かったって喜んでいる子もいます。
　こういうタイプは、理論も基本も関係なく、見たままで勝負して、バンバン活躍する運動センス抜群のタイプかもですね・・・。　バレーは、結果が出れば、あまり難しいこと言う必要はないですからね。
　正解が出なければ、６ｍを導いたこういう子が優勝です。
　
　ほんとに、かわいいですよね。機会があれば、タイプを見分ける意味で子供さんに質問してみてください。

最後に
　実戦では、ややトスが乱れて、アタッカーに余裕がない状態でスパイクされるときや、逆にノーブロックとなって力任せのスパイクを打たれる状況のとき（例えば時間差のセミクイック)などで、こういうパターンが多いですね。

　もちろん、逆にこれを利用して、丁寧にバックラインいっぱいを狙ってくるスパイクもありますから、レシーバーは状況を判断して、待つのか、突っ込むのか判断しなければなりません。アタッカーの心理を読むのも大事です。

　以上です。　今日もありがとうございました。

予告を少し・・・　
　明日から、さらにレシーバーのポジション取りのパターンをスパイクレシーブ→二段トス→ブロックのカバー→センター攻撃マークのポジション（これはすでに下記の記事としてアップしています。）からチャンスボールへのポジション変更という感じで、いくつか説明していきますので、よろしくお願いします。
ポジション取りは、サーブを打つ前から始まる。
相手がサーブカットしたボールがセッターに戻っていくとき（後衛レフト）
相手のサーブカットがセッターに戻っていくとき（後衛センター）
レシーブ陣の動き（後衛ライト）
こちらも↓よろしくお願いします。
 
にほんブログ村