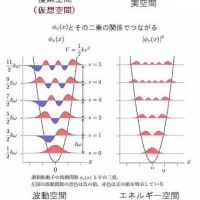
正弦波の表現法
二次元実空間 複素数空間(極座標)


波の合成とその表現法 (二次元実空間と複素数空間の比較)


複素数空間(ガウス平面)で波の合成表現ができる

波の合成をベクトルの合成で表現できる。
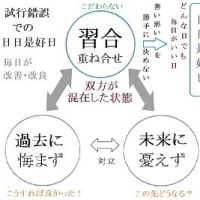
空観方程式ではこの原理を応用して、三位一体の関係を二次元に表現する。
α―β=θが位相項で進行速度を示す。
ちょうど0度で波は最大、90度で消滅し相互作用も無かったことになる。
複素数空間のうま味
三角関数の掛け算では、複素数空間を使えばオイラーの公式により足し算となる事。
↓


シュレーディンガー70年の夢-波動関数の観測-
永山 国昭著
http://ir.soken.ac.jp/?action=repository_uri&item_id=2567&file_id=22&file_no=1
http://ir.soken.ac.jp/?action=repository_uri&item_id=2567&file_id=22&file_no=2
二次元実空間 複素数空間(極座標)


波の合成とその表現法 (二次元実空間と複素数空間の比較)


複素数空間(ガウス平面)で波の合成表現ができる

波の合成をベクトルの合成で表現できる。
空観方程式ではこの原理を応用して、三位一体の関係を二次元に表現する。
α―β=θが位相項で進行速度を示す。
ちょうど0度で波は最大、90度で消滅し相互作用も無かったことになる。
複素数空間のうま味
三角関数の掛け算では、複素数空間を使えばオイラーの公式により足し算となる事。
↓


シュレーディンガー70年の夢-波動関数の観測-
永山 国昭著
http://ir.soken.ac.jp/?action=repository_uri&item_id=2567&file_id=22&file_no=1
http://ir.soken.ac.jp/?action=repository_uri&item_id=2567&file_id=22&file_no=2