神霊写真館
神と悪霊・私が撮影した神様・龍神様・稲荷狐さんの写真館・妖精も写っています。
今の中学校は、部活がまるで「お仕事」の様に生活時間を占めている事には驚きです。
部活が忙し過ぎて、勉強している時間が取れないなんて、これから受験が有るのに、何を考えているのか分かりません。
体調を崩して、塾をお休みする子供が居るくらいです。
私は6歳の時から「芸術家」に成るのが分かっていましたから、習い事が忙しくて部活などはやった事もありません。
私の場合は、ピアノにしろ、声楽にしろ、クラシックバレエにしろ、プロに成る為に必要な訓練でしたので、苦にも無駄にもなりませんでした。
しかし、部活はなんの為にやっているのか、さっぱり分かりません。
バスケット部にしても、卓球部にしても、サッカー部にしも、プロに成れるだけの才能が有って、べつに高校も大学も勉強しなくても
「特待生」で入れるのなら勉強する必要もないでしょうが、普通の子にとっては、勉強の妨げにしかなっていない様です。
部活の顧問によっては、試合で遠征中には勉強禁止を言い渡す者まで居て、子供達は実際に不満を持っています。
あんまりひどいので、部活はやめようと考えている子達も多くいます。
でも、部活をしていないと、「内申点が悪くなる」中学も有るので、それでジレンマに陥って、真剣に悩んでいる有様です。
部活はどうでも、受験は疎かには出来ません。
どこの大学に行ったかによって、入れなくなる企業まで有るのです。
夏休みもなく、毎日毎日夕方まで練習だとか聞かされて、正直、どうなっているのか？疑問と同時に驚きです。
大した意味の無い事に時間を取られて、人生の時間は限りがあるのに、一体教師は何を考えているのか、理解出来ません。
本当に子供達の将来を考えているとは、到底信じられません。
生徒が分からないと言う問題の解き方を載せます。
例題
A、B 2種類のジュースがあり、昨日は合わせて50本売れた。
今日は、昨日と比べて、Aは20%増加し、Bは10%減少した
ので、合わせて54本売れた。
昨日売れた2種類のジュースの本数をそれぞれ求めよ。
昨日、Aはｘ本、Bはｙ本売れたとする。
昨日売れた本数は合わせて50本だから、
x＋y＝50・・・・・・・・①
今日、Aが売れた本数は 120/100x本、Bが売れた本数は
90/100y本で、合わせて54本売れたから、
120/100x+90/100y=54・・・・・②
①、②より、 x＝30 、 ｙ＝20
答 A・・・30本、B・・・20本
２、濃度の問題
４％の食塩水と８％の食塩水がある。
この2種類を混ぜて、５％の食塩水を400g作りたい。
2種類の食塩水をそれぞれ何ｇ混ぜればよいか。
４％の食塩水では、
食塩の重さ＝（食塩水の重さ）×4/100
である。
食塩水の重さと、その中に含まれている食塩の重さに目を
付けて、連立方程式を作れば良い。
４％の食塩水をｘｇ、８％の食塩水をｙｇ混ぜるとすると
x+y=400
4/100x+8/100y=400×5/100
これを解いて、 x=300 y=100
答 ４％の食塩水・・・300ｇ ８％の食塩水・・・100ｇ
連立方程式には＝が二つのものがあります。
例題
6x+3y-10=4x+3y-6=x+y
どう展開するかと言うと
6x+3y-10=x+y・・・①
4x+3y-6=x+y・・・②
①を展開すると
＝の右側を整数にする。
6x+3y-10=x+y→ 整数の－10を右側に移すとーは+に変わる
x+yを左に移すと
6x+3y－x-y=10→5x+2y=10・・・①’
同様に
4x+3y-6=x+y・・・②を展開すると 3x+2y=6・・・②’
①’ー②’ より 2x=4→ ｘ＝２
②’ にｘ＝２を代入して y=0
要点は、式を展開して、=の右側を「整数」にすること。
それだけやれば、あとは簡単！
＝の意味がよく分からない子も居るので説明しておきますが
＝の右側と左側が同じ値であるということです。
たとえば
x - 3 = 5
からｘを求めるには、ｘ以外の数を右側へ移動させれば良いのですが
－３を右側へ移すと、左側から（－３）が減ることに成ります。
だから、ｘ＝５－（－３） になりー×ーはプラスになるので
x = 5 + 3
x = 8
に成ります。
＝の反対側へ移動したら、プラスがマイナスに成る、と単純に覚えないで
理屈が分かってさえいれば、応用問題も解けるようになりますよ！
中1の理科で習う、食塩水の濃度の求め方。
注意
食塩水（溶液）の重さには，水だけでなく，食塩の重さも含まれます．
例 食塩20(ｇ)が水100(ｇ)に溶けているとき，食塩水の濃度は20％ではありません．
食塩水120(ｇ)のうち20(ｇ)が食塩だから，20÷120×100＝16.7（％）です．
例題
８％の食塩水250ｇに含まれる食塩は何ｇか。
食塩の重さ＝溶液×100分の濃度（％）
食塩の重さ＝250ｇ×８/100 =20g
生徒が学校で説明されてなくて分からない、と言うので調べたのでした。
どうしてきちんと授業してくれないのでしょうね？！
教えれば、ちゃんと理解するのにね。ふ・し・ぎ
体積と比
水の容積と底面積と深さの比
容器の中に入っている水などの体積を「容積」といいます。
柱の容器に入れた水の容積が同じならば、底面の面積と深さは逆比になるという法則があります。
柱の容器に入っている水の容積が同じ時
底面の面積の比＝a:bならば、
深さの比＝b:a
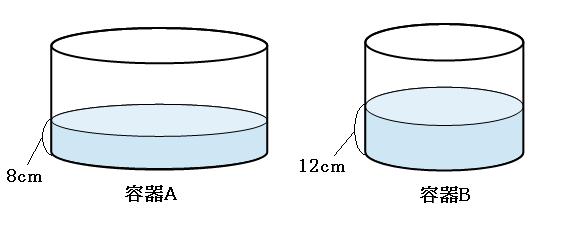
同じ体積の水を円柱の容器Aと容器Bに入れると、容器Aは深さが8cmに、容器Bは深さが12cmになりました。 容器Aと容器Bの底面の面積の比は何対何でしょう。
容器に入っている水の体積は同じなので、底面の面積と深さは逆比になります。
今回は深さの比＝8cm:12cmなので、
底面の面積の比＝12:8
＝3:2
よって答えは
3:2
＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿
これが中学入試の問題です。
中学数学に出てくる「円柱の体積の求め方」
底面積×高さ
これは超簡単です。中学入試の問題よりも簡単かも？
ちょっと面倒臭いのは、円柱の体積の比較問題です。
問題
底面の半径がｒｃｍ、高さがｈｃｍの円柱Aと、底面の半径がAの２倍で、高さがAの１/２の円柱Bがあります。
Bの体積はAの体積の何倍になるかを、文字式を使って説明しなさい。
A=πr²h
B=π✖︎2r×2r×1/2h だから、２×２×1/2=2 と成り
(πr²h は 割算で消滅するので、数字だけ残る。)
答えは Bの体積はAの二倍
これは中２の問題で、生徒が現在やっているので、説明したところです。
今日は、学校の教科書には出てこない、少々面倒臭い答えが出る、ショウイン式の問題集の一部を書いてみます。
ショウイン式の問題は公立学校では出ない難度の問題がいっぱい有るのです。
只の「分数を含む連立方程式」でも、えっ？！こんな答えで良いのかな？と計算していて悩んでしまう様な問題です。
x+6y/4=10 ４分のｘ+６ｙ＝１０・・・①
x-3y/3=5 ３分のｘ-３ｙ＝５ ・・・②
まず 分母を外します。
①には４を掛けて x+6y=40・・・・・①’
②には３を掛けて x-3y=15・・・・・②’
①’から②’を引くと 9y=25➡y=25/9
これでｙの解が出たので、これを②’に代入する。
x-3(25/9)=15 ➡ x-25/3=15
➡x=15+25/3 ➡45/3+25/3 = 70/3
答えは x=70/3、y=25/9
生徒が教科書の問題には、もっと割り切れる数が答えなので、計算してみてから、
「あれっ？！これで良いのかな？！」
と思ってしまうそうです。
ショウイン式は全国区だから、学力テストには強いのですよ～！
まず、方程式とは何でしょう？？
わからない文字（例えばｘ）などを含む等式 ( = がある式)
のこと、たとえば、x−１= 0 みたいな。
方程式を解く、とは、ｘに何が入るかを求めることです。
二元一次方程式とは
2種類の文字＝元 が入っていて、1つの項あたり最大1回文字がかけられている方程式
ｘとｙ それが1回掛けられている
たとえば、
2x – 5y = 26 みたいな方程式のこと。
そして、連立方程式とはなんでしょう？！
二個以上の未知数を含む二つ以上の方程式の組。それらの方程式を同時に成り立たせる未知数の値の組をこの連立方程式の解といい，解をすべて求めることを連立方程式を解くという。未知数に関する最高の次数により連立一次方程式・連立二次方程式などという。
大辞林から。
次に、連立方程式の解き方を説明します。
連立方程式には 加減法や代入法 があります。
連立方程式の解き方では、2つある文字を1つ消去することが基本になります。
中1数学でならった「一次方程式」の解き方を使うためです。
例題
次の連立方程式を解きなさい。
2x+3y = 16・・・・①
x + 7y = 19・・・・② ➡２倍してｘの値を①と同じにする
まずは文字を1つ消去する
消去する方法はつぎの2つがあります。
- 加減法
- 代入法
どちらでも良いけど、加減法の方が簡単です。
x + 7y = 19・・・・② ➡２倍してｘの値を①と同じにする
２x+14ｙ＝38・・・②”
2x+3y = 16・・・・①から②”を引く
２x+14ｙ＝38
yだけの -11 y = -22 という方程式になります。
一次方程式をといてみましょう！
yの係数（-11）で両辺をわると、Y=2という解に成ります。
ｘを求めるには、Y=2 を代入しましょう！
x + 7y = 19・・・・②
Yに２を代入すると、ｘ+７×（２）＝１９
ｘ+14＝19
だから、X=19－14＝５
これでXY両方の解が出ました。
ｘ＝５、ｙ＝２
解き方は
- 文字を消去
- 一元一次方程式をとく
- 代入する
の３ステップを覚えれは良いのです。
あと、分数や小数の入った方程式も有ります。
ちょっと面倒です。
私は数学のテストはいつも、一番難しい問題だけは解けていた変わった子供でした。
と言うのも、小学校の時の担任に、一人も理数系の教師が居なくて、新しく公式が出てきても、まるで説明してくれずに
「なんでもいいから、当て嵌めればいいんだ～！」
なんて言う始末。
何がどうしてこうなったのか？！と言う説明が無いと、一体この数や文字（ｘ、ｙ）は何処から出てきたのだろうか？
と言う疑問だらけで、分からないものは使えないので、公式は使えない生徒に成ってしまいました。
でも、学校で教えられる公式は当て嵌まらない難しい問題は、自分の頭で論理的に考えて処理できるので、いつも出来ていたのでした。
高校に入ってからの数学教師は良い先生で、ちゃんと説明してくれたので、公式が使える様になり、
「なんだ、こんなに簡単なことだったのか！！」
と腹が立ちました。 あ～あ、損した！と思いましたよ。
先生によって、面白くもなり、訳が分からない事にもなり、教える人の技量は重大なのです。
父が数学が一番簡単なんだよ！と言っていたのが本当でした。
中１の問題で
「式の値の利用」音速の求め方、と言うのがあります。
これが分からないと生徒に言われて、以下、３つの問題を教えたのでした。
音が空気中を伝わる速さは、気温によって変化し、気温がｔ℃のときの音の速さは
( 331.5+0.6t)m/s で表すことができる。
ｔ＝気温 temperature
※“ｍ／ｓ”は“メートル毎秒”と読み、１秒間に進む速さを表す単位です。
①気温が15℃の時の音の速さを求めなさい。
331.5+0.6×15=340.5(m/s)
②気温が25℃の時、雷が光ってから4秒後に音が聞こえた。
その場所までの距離を求めなさい。
音の速さは331.5+0.6×25＝346.5(m/s) だから、
雷までの距離は 346.5×４＝1386(m)
③気温が20℃のとき、4秒間に音が空気中を伝わる距離を求めなさい。
音の速さは331.5+0.6×20＝343.5(m/s) だから
4秒間に空気中を伝わる距離は
343.5×4＝1374(m)
音速について補足
空気中を伝わる音の速さは
◇１気圧で、気温が０℃という条件なら、毎秒３３１．５ｍ です。
そして、気温が１℃上がるごとに毎秒０．６ｍずつ速さが増していくという実験データがあります。
◇音の速さ＝３３１．５＋０．６×［気温］（ｍ／ｓ）
空気が温かくなるほど、速さも増していきます。ただし、現実の世界の「天気」は、場所によって細かく違います。
音が１秒間に３００ｍ 以上進むといっても、この約３００ｍの間、「空気の状態」がずっと同じとは限らないのですが、
計算をシンプルにするために、風の影響はいったん無視し、音が伝わる間は「すべて同じ状態」と考えようと言う事で
気温は、地球の平均気温である「１５℃」という設定にしよう、と言う事に成りました。それにより
３３１．５＋０．６×１５＝３４０．５（ｍ／ｓ）
「音の速さは秒速約３４０ｍ」となったのです。
ｔなるものが何なのか、0.6と言う数字は何処から出て来たのかを説明されれば
実際のところ、全然難しくはありません。
これが時差の公式ですが、分母に成っている１５はどこから出てきたのでしょうか？
これは
地球の1回転＝360度
それを一日は24時間だから、360÷24＝１５
つまり、15度で1時間の時差が出る事に成ります。
そこからこの１５と言う数が出てきました。
中学の中間テストにこの「時差を求める問題」が出るのですが、学校では公式について説明してくれないそうです。
それで調べたら、公式に使われている数字の意味が分かりましたので、掲載いたします。
私の子供の頃も、学校の先生は、数学の公式についても何も説明してくれなくて、先生なんぞは大嫌いでしたが、今の小中学校でも、大事な事を全然教えない教師が多く存在しているそうです。
そして、教えもしないのに、テストには出題するとは、教師失格です。
「生徒の悩み相談室」には喜んで成りましょう！
「魔法陣」とは
たて・よこ・ななめ、どの線に沿って足してもその合計が同じような方陣のことを言います。
図の8と12の和と、9とアの関係からアに入る数を求めなさい。
左の縦のライン＝８+１２+□ と９+ア+□ の合計は同じです。
このことから、8+12＝9+ア なので、20＝9+ア
だから、ア＝20-9＝１１
ア＝１１ になります。
これで８の斜めラインは8＋11＋□
右端の縦ラインは9+✕＝8+11なので
✕＝19-9＝１０
これで、真ん中の横ラインは
12+11+10 だと分かったので
合計は３３になります。
後は、縦横斜めが33に成る様に図を埋めて行けば
魔法陣は完成します。
これが中一の数学の中間テストに出たのです。
参考までに・・・・
