Part0アサルトキャノン予定立てとか。
Part1アサルトキャノンのもろもろ性質とか。
Part1.5アサルトキャノン射程について。
Part2アサルトキャノン攻撃力のPA依存性について。
Part3アサルトキャノン攻撃力のAA攻撃力/OB依存性について。
Part3.01レギュ変化に伴い心機一転
Part4PA16000~19555でのアサルトキャノン攻撃力
Part5PA12000~16000でのアサルトキャノン攻撃力
Part5.5Part4,5における計算式の改変
Part6PA9000~12000でのアサルトキャノン攻撃力
Part7PA9000以下のアサルトキャノン攻撃力とまとめ
今回は、アサルトキャノン攻撃力のAA攻撃力/OB依存性についてです。
PA18410の機体でAA攻撃力/OBを7種取って各自攻撃力の距離減衰近似式を立てて、傾きと切片を求めます。誤差の出方は過去記事参照。どんどん細かい説明めんどくさくなってきちゃう。
まず、アサルトキャノン攻撃力の傾向を距離別にグラフで示します。
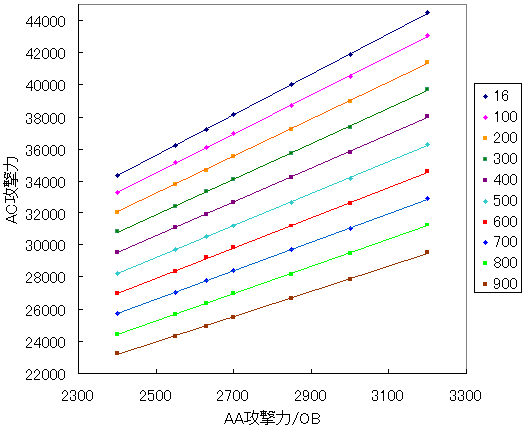
PAを変化させたときとは異なり素直な直線ばかりですね。
距離を変数とした近似直線の傾きと切片のデータをAA攻撃力/OB別に以下に示します。

傾きの近似式は、
傾き = -0.005274×AA攻撃力/OB - 0.047738 R^2 = 0.999900
上式での切片は、全体に占める割合はごくわずかです。そこで、アサルトアーマーのときにはお馴染みだった切片操作を行います。
切片=0にします。
傾きの近似式とそのグラフは以下のようになりました。

一方、切片の方はどうでしょう。

こちらは普通に一定の切片-切片を持った直線です。
Part2からの一連の流れを見て既にお気づきの方もいらっしゃるとは思いますが、アサルトキャノン特有の与ダメージのばらつきがあるとはいえ、攻撃力の変化の傾向はアサルトアーマーのときと全く一緒です。傾きがAA攻撃力/OBに正比例して、特定PA間で傾向が変化する、そして切片はPA値によって変化する(切片-傾き)と一定の(切片-切片)を持ったきれいな直線になる。ということは、ばらつきを考慮しないアサルトキャノンの攻撃力の式もアサルトアーマーと同じような、
アサルトキャノン攻撃力={(距離+A)(B×PA+C)+D}×AA+E×PA(A~Eは実数)
という式になるのではないかと予想できます。こうなればいいんだけど実際どうだか。実際その誤差ってヤツが厄介なの何の。最終的な式を求めるには、やはりこれもアサルトアーマーと同レベルの7×11の77機体は最低でも使って求める必要が出てきそうです。今後はAA攻撃力/OBをメインの変数に据えてPAを変化させるというAAのときと同じ方針を予定しています。
ME☆N☆DO☆KU☆SA☆I
ちなみに、アサルトアーマーとアサルトキャノンの攻撃力比較をしてみるとどうなるだろうってのが↓。PAが18410のとき。ぶっといのがアサルトアーマーの段数別の攻撃力。段数の定義は「アサルトアーマーりべんじ」シリーズ参照。
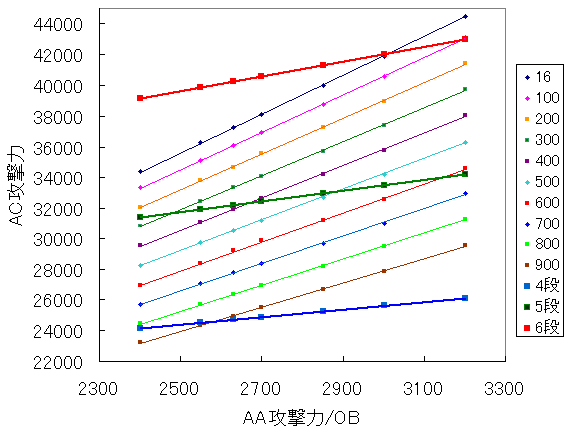
PA18410のとき、アサルトキャノンが命中しうる距離をかなりひいき目に300以内と考えればAC攻撃力はアサルトアーマー5段ヒット時と同程度、あるいはそれ以上は出るってことです。アサルトアーマーが5段ヒットするために近づかなければいけない距離は、PA18410でAA範囲/OBが100の場合で距離86未満です。6段ヒットするには同条件で67だか68未満ぐらい。
もうちょっと弾速あればアサルトキャノンは脅威になりうるんだけどな…。
アサルトキャノン/Part3.01心機一転
Part1アサルトキャノンのもろもろ性質とか。
Part1.5アサルトキャノン射程について。
Part2アサルトキャノン攻撃力のPA依存性について。
Part3アサルトキャノン攻撃力のAA攻撃力/OB依存性について。
Part3.01レギュ変化に伴い心機一転
Part4PA16000~19555でのアサルトキャノン攻撃力
Part5PA12000~16000でのアサルトキャノン攻撃力
Part5.5Part4,5における計算式の改変
Part6PA9000~12000でのアサルトキャノン攻撃力
Part7PA9000以下のアサルトキャノン攻撃力とまとめ
今回は、アサルトキャノン攻撃力のAA攻撃力/OB依存性についてです。
PA18410の機体でAA攻撃力/OBを7種取って各自攻撃力の距離減衰近似式を立てて、傾きと切片を求めます。誤差の出方は過去記事参照。どんどん細かい説明めんどくさくなってきちゃう。
まず、アサルトキャノン攻撃力の傾向を距離別にグラフで示します。

PAを変化させたときとは異なり素直な直線ばかりですね。
距離を変数とした近似直線の傾きと切片のデータをAA攻撃力/OB別に以下に示します。

傾きの近似式は、
傾き = -0.005274×AA攻撃力/OB - 0.047738 R^2 = 0.999900
上式での切片は、全体に占める割合はごくわずかです。そこで、アサルトアーマーのときにはお馴染みだった切片操作を行います。
切片=0にします。
傾きの近似式とそのグラフは以下のようになりました。

一方、切片の方はどうでしょう。

こちらは普通に一定の切片-切片を持った直線です。
Part2からの一連の流れを見て既にお気づきの方もいらっしゃるとは思いますが、アサルトキャノン特有の与ダメージのばらつきがあるとはいえ、攻撃力の変化の傾向はアサルトアーマーのときと全く一緒です。傾きがAA攻撃力/OBに正比例して、特定PA間で傾向が変化する、そして切片はPA値によって変化する(切片-傾き)と一定の(切片-切片)を持ったきれいな直線になる。ということは、ばらつきを考慮しないアサルトキャノンの攻撃力の式もアサルトアーマーと同じような、
アサルトキャノン攻撃力={(距離+A)(B×PA+C)+D}×AA+E×PA(A~Eは実数)
という式になるのではないかと予想できます。こうなればいいんだけど実際どうだか。実際その誤差ってヤツが厄介なの何の。最終的な式を求めるには、やはりこれもアサルトアーマーと同レベルの7×11の77機体は最低でも使って求める必要が出てきそうです。今後はAA攻撃力/OBをメインの変数に据えてPAを変化させるというAAのときと同じ方針を予定しています。
ME☆N☆DO☆KU☆SA☆I
ちなみに、アサルトアーマーとアサルトキャノンの攻撃力比較をしてみるとどうなるだろうってのが↓。PAが18410のとき。ぶっといのがアサルトアーマーの段数別の攻撃力。段数の定義は「アサルトアーマーりべんじ」シリーズ参照。

PA18410のとき、アサルトキャノンが命中しうる距離をかなりひいき目に300以内と考えればAC攻撃力はアサルトアーマー5段ヒット時と同程度、あるいはそれ以上は出るってことです。アサルトアーマーが5段ヒットするために近づかなければいけない距離は、PA18410でAA範囲/OBが100の場合で距離86未満です。6段ヒットするには同条件で67だか68未満ぐらい。
もうちょっと弾速あればアサルトキャノンは脅威になりうるんだけどな…。
アサルトキャノン/Part3.01心機一転









