Part1レギュ1.30でのAA攻撃力計算に先立ち
Part216000≦PAのAA攻撃力式
Part312000≦PA≦16000のAA攻撃力式
Part49000≦PA≦12000のAA攻撃力式
Part5PA≦9000のAA攻撃力式
Part6AA攻撃力計算式まとめ
Part7PA満タン以外でも計算式を成立させる
Part6はPart2~5のまとめです。
各PAでのアサルトアーマー攻撃力は、
段数=Z、整波性能値=PA、AA攻撃力/OB=AAとして、PA値によって値のとり方の異なる定数B、Cを用いると、
アサルトアーマー攻撃力={(Z-1)(B×PA+C)+0.30}×AA+0.12×PA
B×PA+C
=2/45×10^(-5)×PA-0.020 (PA≦9000)
or
=2/15×10^(-5)×PA-0.028 (9000≦PA≦12000)
or
=1.0×10^(-6)×PA-0.024 (12000≦PA≦16000)
or
=-8.0×10^(-3) (16000≦PA)
P-MARROW装備時はAA→AA×2.00になる(レギュ1.30現在)
ヒット数Z=(1,2,3,4,5,6)で、
総合アサルトアーマー攻撃力=Z×[{(Z-1)(B×PA+C)/2+0.30}×AA+0.12×PA]
ちょっとやったら過去記事よりも変数を一つ減らせたので多段ヒットの式の形を簡潔にしました。
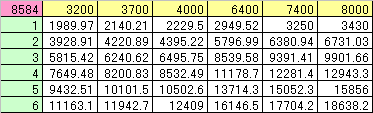
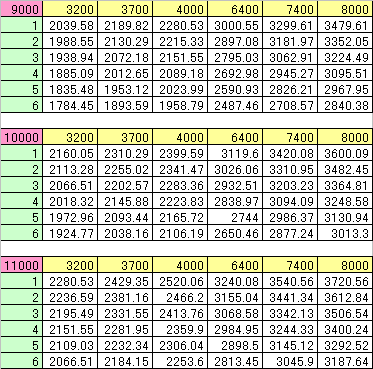
まだ一連の流れで示していませんでしたが、AA攻撃力/OBを固定してPAを変えていく場合、総合AA攻撃力はどのように変化していくでしょうか。全部やるだけのスペースも無いので、6ヒットしたときの、AA攻撃力/OBが3200、3700、4000、P-MARROW装備で6400、7400、8000で計算して表記すると、

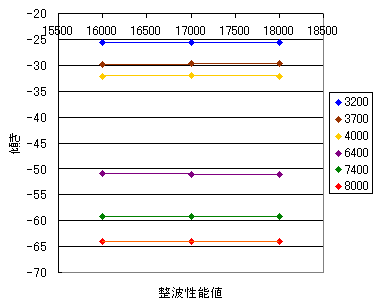
グラフは、

他のAA攻撃力/OBの場合でも帯状の線で囲われた中の攻撃力をとる。P-MARROW無しだと下の帯、有りなら上の帯。1.30では長時間PAが剥げるリスクに対し、最大でもこのぐらいのリターンがあるということです。1.20と比べてずいぶん落ち着きました。
【ACfA】アサルトアーマー解説?動画【レギュ1.30】
作ったので早速はりつけ。クリティカルとか口で言うよりわかりやすい。
Part7PA満タン以外でも攻撃力計算式を成立させる。
Part216000≦PAのAA攻撃力式
Part312000≦PA≦16000のAA攻撃力式
Part49000≦PA≦12000のAA攻撃力式
Part5PA≦9000のAA攻撃力式
Part6AA攻撃力計算式まとめ
Part7PA満タン以外でも計算式を成立させる
Part6はPart2~5のまとめです。
各PAでのアサルトアーマー攻撃力は、
段数=Z、整波性能値=PA、AA攻撃力/OB=AAとして、PA値によって値のとり方の異なる定数B、Cを用いると、
アサルトアーマー攻撃力={(Z-1)(B×PA+C)+0.30}×AA+0.12×PA
B×PA+C
=2/45×10^(-5)×PA-0.020 (PA≦9000)
or
=2/15×10^(-5)×PA-0.028 (9000≦PA≦12000)
or
=1.0×10^(-6)×PA-0.024 (12000≦PA≦16000)
or
=-8.0×10^(-3) (16000≦PA)
P-MARROW装備時はAA→AA×2.00になる(レギュ1.30現在)
ヒット数Z=(1,2,3,4,5,6)で、
総合アサルトアーマー攻撃力=Z×[{(Z-1)(B×PA+C)/2+0.30}×AA+0.12×PA]
ちょっとやったら過去記事よりも変数を一つ減らせたので多段ヒットの式の形を簡潔にしました。
まだ一連の流れで示していませんでしたが、AA攻撃力/OBを固定してPAを変えていく場合、総合AA攻撃力はどのように変化していくでしょうか。全部やるだけのスペースも無いので、6ヒットしたときの、AA攻撃力/OBが3200、3700、4000、P-MARROW装備で6400、7400、8000で計算して表記すると、

グラフは、

他のAA攻撃力/OBの場合でも帯状の線で囲われた中の攻撃力をとる。P-MARROW無しだと下の帯、有りなら上の帯。1.30では長時間PAが剥げるリスクに対し、最大でもこのぐらいのリターンがあるということです。1.20と比べてずいぶん落ち着きました。
【ACfA】アサルトアーマー解説?動画【レギュ1.30】
作ったので早速はりつけ。クリティカルとか口で言うよりわかりやすい。
Part7PA満タン以外でも攻撃力計算式を成立させる。