広島・長崎、原爆73年後の真実(2) - 長崎の原爆はなかった

本日8月9日は長崎の原爆の日。広島とも合わせ犠牲になった全ての犠牲者のご冥福と、ご遺族の心の安寧をお祈りしたいと思います。


さて、長崎の原爆の日ということで、今回は長崎に投下された原爆で使用されたという原子爆弾「ファットマン」について考えてみたいと思います。


ファットマン

■ファットマンの起爆構造

ファットマンでは爆薬にプルトニウムが用いられることは有名ですが、その起爆装置に爆縮レンズが使用されていた(とされている)ことは、どれくらいの方がご存知でしょうか？要するに、分散配置されたプルトニウムを、一般のレンズが光を一つの焦点に集めるが如く、火薬の爆発力で一点に集め、それによって超臨界状態を起し、核爆発を誘発させようとするものです。

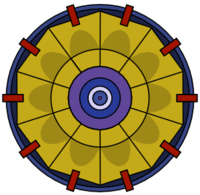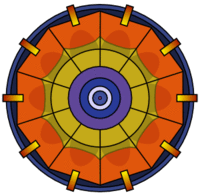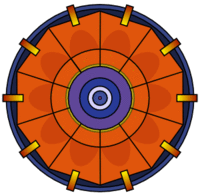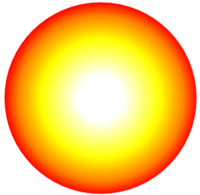
色の濃いコブ状の部分が「遅い火薬」。これにより点火位置と中心を結んだラインでは到達速度が遅くなる。また、点火位置から点火ユニットの端を通り、遠回りして中心に至るラインでは速い速度が維持され、結果として中央ユニットに同時に爆発が到達する。

引用元：Wikiペディア https://ja.wikipedia.org/wiki/%E7%88%86%E7%B8%AE%E3%83%AC%E3%83%B3%E3%82%BA

さて、この爆縮レンズ、米国機関がジョン・フォン・ノイマンなどの数学者を総動員して設計したことで有名です。この設計に関る米ソのスパイ合戦などは、時々ドキュメンタリーなどで報道されていました。設計に関するくだりをWikiペディアから引用すると

ZNDモデルでは先行する衝撃波は不連続面として扱われるが、双曲型偏微分方程式を差分近似で数値的に解こうとすると衝撃波の不連続面は特異点になってそこで解が発散してしまい計算することが出来なくなってしまう。そこでジョン・フォン・ノイマンは人工粘性の概念を取り入れることで上放物型偏微分方程式の差分近似に置き換えて計算することに成功した。その結果、曲がりなりにも衝撃波の数値計算ができるようになった。しかし、ZND理論は大変に複雑で膨大な計算を要したため1940年代当時のロスアラモス研究所に集められたジョン・フォン・ノイマンらの数学者達の手によっても、優に10ヶ月以上の時間を要した。当時は、コンピュータが無かったためである。

計算の結果、点火装置の数と、それに応じるように配置された火薬のコブは、原子爆弾一つにつき32個が最適であると結論された。しかし、当時の起爆装置では32個の雷管を同時起爆する際に生じる誤差をナノ秒単位に収めることが出来なかった。そのため、新しく起爆電橋線型雷管が開発された。

ここで注目するのは強調した部分、「当時は、コンピュータが無かった」、「同時起爆する際に生じる誤差をナノ秒単位に収める」の2点です。続いて、同引用文中に書かれている起爆電橋線型雷管について、同じくWikiペディアを引いてみましょう。

起爆電橋線型雷管(きばくでんきょうせんがたらいかん 英:Exploding Bridge Wire detonator、略称:EBW)とは、マンハッタン計画の一部として、1940年代にロスアラモス国立研究所で爆縮レンズ用に極めて正確に作動する雷管としてルイス・アルヴァレズによって開発された。

原子爆弾に使用する爆縮レンズは数十マイクロ秒以下の誤差で正確に起爆する必要があったが、普通の電気雷管では電熱線の加熱によって点火薬を発火させていたため、通電から起爆まで200～300ミリ秒もかかり、通電から起爆までに100ミリ秒以上の誤差があった。衝撃波は1ミリ秒につき7～8メートルも進むため、僅か1ミリ秒の誤差でもプルトニウムがバラバラになって飛び散り、核分裂は起きないため原子爆弾には使えなかった。そのため、新たな方式の起爆装置を開発する必要に迫られて、新型雷管が開発されることになった。このような事情から、新型雷管には誤差0.1マイクロ秒以下の精度が要求された。

・・・・中略・・・・

最終的な精度は0.025マイクロ秒にまで高められたと言われている。

なんとこちらでは、「原子爆弾に使用する爆縮レンズは数十マイクロ秒以下の誤差で正確に起爆する必要があった」と先の引用文のナノ秒単位とは随分と記述内容に違いがありますが、どちらが本当なのでしょう？幸い上記引用文の最後に「新型雷管には誤差0.1マイクロ秒以下の精度が要求された」そして、伝聞情報としてですが、「最終的な精度は0.025マイクロ秒にまで高められた」とあります。こちらが前引用と整合しますので、こちらに沿って考えたいと思います。


■起爆許容誤差時間について考える

ここで単位についてのおさらいです。

　1 マイクロ秒：1 / 10⁶ = 1 × 10^-6　百万分の1秒 →　記号μs
　1 ナノ秒：　　1 / 10⁹ = 1 × 10^-9　十億分の1秒 →　記号ｎs

よって、文中の具体的な数値をナノ秒単位に揃えると

　0.1μs以下　→　100ｎs以下
　0.025μs 　→　 25ｎs

となります。以上より、当時達成された起爆時間の許容誤差は、概ね 25～100ｎsの範囲と推定されます。

ここで、この微小時間の測定について考察します。最初に、この時間を測定するための精度、目盛りの大きさについて見てみましょう。

仮に、1.2cmの物体の長さを測るのに、物差しにどれくらいの目盛幅が必要でしょうか？ここでは目分量による概算はできないとします。正確に測りたいなら、mm単位の目盛りが必要なのは誰でも分かると思います。仮に1cmの目盛幅しかないなら、切り下げて1cm、切り上げて2cmと測定されることになります。

これは時間の計測ですから、定規のような目盛りを用意することはできません。その代わりとなるのが時計ですが、普通の時計では時の刻みが秒単位ですから、とてもじゃないけどナノ秒を表現することはできません。現代では水晶発振器などを用いて、極小単位の時を刻むことが可能です。パソコンやスマホに搭載されているCPU(中央演算回路)も基本的にこの発振器と同期して動いています。これをクロック周波数と呼ぶことは、コンピュータがお好きな方はどなたもご存知かと思います。一般に周波数が高ければCPUの演算能力は高い(速い)とされています。

現在ではクロック周波数でギガヘルツ(GHz)単位の高速CPUが普通に購入できます。ありがたいものですね、今や Java や Pythonなどの汎用プログラミング言語でも、ナノ秒単位の測定プログラムが当たり前に組めるのですから。ちなみに1GHzの振動数と、1振動における時間(時間の目盛りとなる刻み幅)の関係は以下のようになります。

　1GHz：1 × 10⁹ 回毎秒
　刻み：1 / 10⁹ = 1 × 10^-9 = 1ｎs

ここでさらに、クロック周波数と時間の刻み幅の関係をまとめてみました。なおMHzはメガヘルツと読みます。

　 10MHz → 100ｎs
　100MHz → 10ｎs
　 1GHz → 1ｎs

そうすると、誤差精度10ｎsオーダーの時間のずれを測定するのに100MHzオーダーのクロック周波数、25ｎsなど1ｎs単位の誤差が本当に測定できたとしたなら、1GHzオーダーのクロック周波数を発生させる発振器が最低でも必要となります。


■爆縮レンズは製造できなかった

CPUの産業史を振り返ると、1970年代にインテルが発表した演算回路8080でさえそのクロック数は5-10MHzで基本的にマイクロ秒単位の計測しかできません。現在一般用途で使われている水晶発振器もせいぜい20MHz程度です。何を言いたいかというと、原爆製造当時、どうやって100MHz以上の高周波数の発振器を調達したのか、そこに大きな疑問があるということです。仮に軍事用の超スペシャルな技術で高周波発振器を得たとしても、「当時は、コンピュータが無かった」という状況ですから、アナログ回路だけでどうやってそれを数値化したのかが不明です。


Intel 8080

ちなみに電気工学に詳しい方にお聞きしたところ、「アナログ回路でナノ秒単位の計測回路を作るのは絶対に無理」と即答されました。

そんなことがわかってくると、はっきり言って、当時の状況としては、原爆開発よりも、このレベルの時間計測器を発明する方がよっぽど革命的な技術革新だったのではないかとさえ思えてくるのです。

それに加え、爆縮レンズを製造する加工精度はどうだったのかも気になります。起爆タイミングがｎsレベルの誤差しか許されないなら、構造物そのものの加工も超絶レベルの精度が要求されると考えられます。特に32面体の各面からの射出角の僅かなズレなどは致命的なものとなるでしょう。追々、それらの誤差許容範囲も計算してみようと思います。そして、このような超高精密爆弾をたった1回のトリニティ実験の成功で実戦投入可能と判断し、起爆方式も違うのに、広島・長崎と立て続けに成功させるその確率たるや、生産工学的には奇跡としか言いようがありません。思い浮かぶ疑問は幾つもありますが、ここでは時間計測の推論だけで充分に以下の結論を出せると思います。

当時の技術で爆縮レンズなんか作れやしない、つまり

　長崎で核爆発なんてなかった

というか、そもそも核爆弾なんて昔も今も存在しないよね？

　*　*　*


以上の推論から、一昨年の記事「改ざんの日本史－長崎原爆投下の真実(1)」にて掲載した。地上起爆に偏った見解は訂正いたします。その後の調査と考察により爆発の中心は、平和公園よりもう少し南西寄りの辺りであったと推測されます。核爆発の可能性が薄れた以上、そもそも一点を基点に爆発したかどうかも分からないので、現在は正確なグランドゼロ(爆心)を求めることに大きな意味はないと感じています。

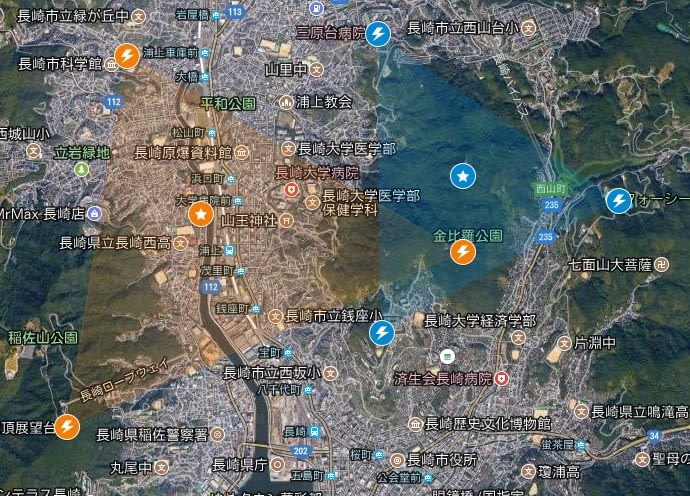
核爆発でなければ何が起きたのか？それについては、また次の記事以降の掲載といたしますが、広島の時と同じように、答のヒントをここに残しておきたいと思います。三角形が2つ描かれていますが、それがどういうことかもよくお考えください。そして、もう一つお題を。広島と長崎の両都市で当時共通していた社会インフラは何でしょうか？ヒントは今も共通しているです。もう、お解かりですね。よろしくお願いします。



キリストの御国にて記す
管理人　日月土