久しぶりに息子の話。
二年前に入学した大学に幻滅して、昨年に別の大学へ入り替えた息子。熱心に勉強する学生が多くて環境が良いと喜んでいるが、勉強好きな学生が多ければ、また別の悩みもあるそうなので紹介しよう。
息子が入った学部は本人特定の恐れがあるので書かないが、卒業すればBachelor of Arts (学士(教養))となる。
学部から貰った選択科目の一覧へ理科関係は無かったそうだが、理系のA学部とB学部向けの某講義を講師へお願いして受講。(息子の話では希望に沿って柔軟に対応されるそうだ。)
先日テストがあり、本人はせめて5割の得点が欲しいと頑張ったつもりだったが、息子の得点は20点台。(T_T)
下のグラフは息子の大学だと比較的入り易いと言われる理系のA学部の学生の得点分布。

息子は赤い棒の位置だが平均点を超えており、ここだけ見るとまあまあの得点に見える。
評価はA~Dの4段階だが、赤い位置ならCは貰えそう。
こちらの下のグラフは息子やA学部と一緒に受講している理系の難関B学部の学生の得点分布。
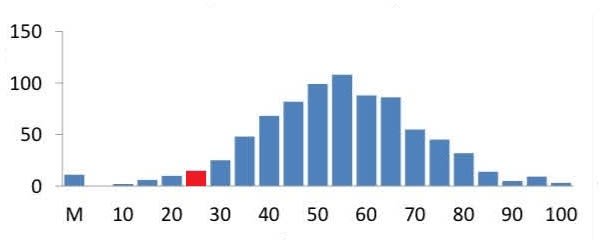
これならF(不可)確実。(ノД`)シクシク
そしてこちらがA学部やB学部の全受講者を合わせた得点分布。
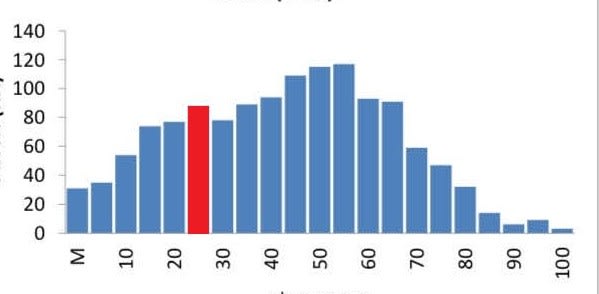
F(不可)にはならないが、最低評価のDは間違い無いだろう。
息子は中学生の頃からこの科目は得意で、試験前も「B学部に負けないぞ!」と勉強しており、まさかこうなるとは思ってなかったそうだが、「学部から示された選択科目以外をお願いして受講し、この成績は無いよな。 orz 」と赤面中。
友達は「理系じゃないのにA学部の平均を超えれば十分」と慰めてくれたそうだが、息子は自分の実力の無さに納得出来ない様子。
息子は今回の受講をW(停止)にして、次の学期か夏休みに再受講を狙いたいらしいが、私は「レベルが大きく違うのだから、同じ講義を受けても受け取り方が違ったり理解の深さも違うよな。再受講しても同じ成績じゃね?」と、実力不足を認めさせる方向で説得中。
同じ大学でもレベルに開きがあり、難関の学部と一緒の講義だと、合わせて相対評価されるので苦労するみたいだ。
息子へは「卒業できれば十分だから、頑張れー!!!」と言っている。w
さて久しぶりに先週出題した数学の解答。
前回の問題

式の値を求めなさい。
メンカームの解答
友達が通う塾の宿題だったそうで、教えを請われた娘が困って私へ連絡してきたが、このパターンの問題は一度やった事があっても解法を思い出せない。
私の返事が遅いので娘は自分で取り組み、分数の繰り返し部分(2ー1/…)が1なら辻褄が合うのに気付き、友達へ4だと答えたそうだが、択一式問題なら満点が貰えても、記述式だと部分点しか貰えない。
私が「分数の繰り返し」で検索すると『連分数』と言うのが判ったが、ウィキペディアの連分数のページを見ても私の頭ではさっぱり意味不明。YOUTUBEで動画を検索してようやく解り易い解説動画を見つけた。
【無限に続く2つの式】連分数と√1+√1+√1+…の計算
動画を参考に解いてみる。
下の式で赤く囲った部分をAとすると…
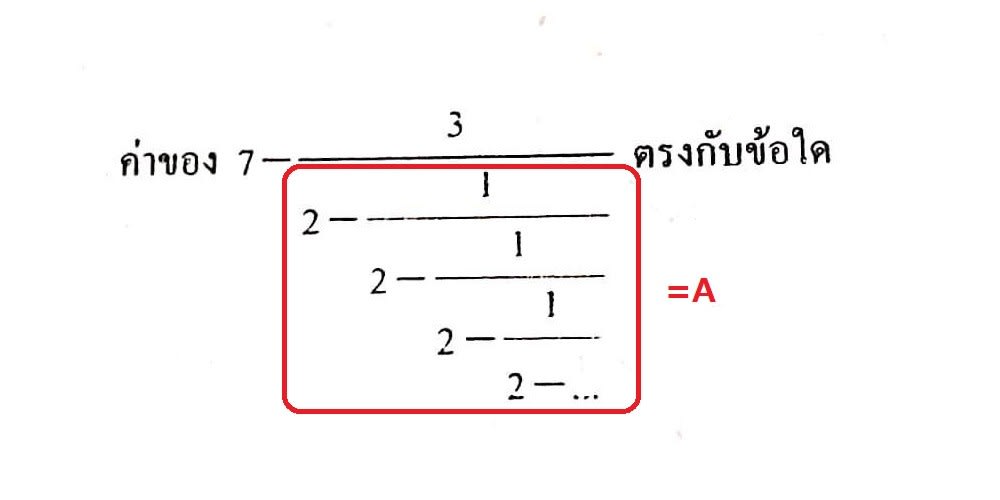
同じ分数の繰り返しなので、下の式で青く囲った部分もAと表せる。
すると上の式で赤く囲った部分は 2ー(1/A)=A となり、これを解くとA=1となる。

分数の繰り返し部分(2つ上の式で赤く囲った部分)をAとすると、与式は 7-(3/A) であり、A =1なので4となる。

答え 4
ムガさんところのお兄ちゃん、正解です。\(^o^)/
#連分数 #中学数学
タイの中学生向け数学ギフテッド問題の記事へのリンク→#高1入試ギフ
貴方のクリックとコメントが、このブログのパワーの源です。
下のバナーへ応援クリックをお願いします。
 海外生活ブログ タイ情報 人気ランキングはこちら
海外生活ブログ タイ情報 人気ランキングはこちら
リアルタイムに更新される新着記事一覧(右下)からタイの今が見える。お薦め。

二年前に入学した大学に幻滅して、昨年に別の大学へ入り替えた息子。熱心に勉強する学生が多くて環境が良いと喜んでいるが、勉強好きな学生が多ければ、また別の悩みもあるそうなので紹介しよう。
息子が入った学部は本人特定の恐れがあるので書かないが、卒業すればBachelor of Arts (学士(教養))となる。
学部から貰った選択科目の一覧へ理科関係は無かったそうだが、理系のA学部とB学部向けの某講義を講師へお願いして受講。(息子の話では希望に沿って柔軟に対応されるそうだ。)
先日テストがあり、本人はせめて5割の得点が欲しいと頑張ったつもりだったが、息子の得点は20点台。(T_T)
下のグラフは息子の大学だと比較的入り易いと言われる理系のA学部の学生の得点分布。

息子は赤い棒の位置だが平均点を超えており、ここだけ見るとまあまあの得点に見える。
評価はA~Dの4段階だが、赤い位置ならCは貰えそう。
こちらの下のグラフは息子やA学部と一緒に受講している理系の難関B学部の学生の得点分布。

これならF(不可)確実。(ノД`)シクシク
そしてこちらがA学部やB学部の全受講者を合わせた得点分布。

F(不可)にはならないが、最低評価のDは間違い無いだろう。
息子は中学生の頃からこの科目は得意で、試験前も「B学部に負けないぞ!」と勉強しており、まさかこうなるとは思ってなかったそうだが、「学部から示された選択科目以外をお願いして受講し、この成績は無いよな。 orz 」と赤面中。
友達は「理系じゃないのにA学部の平均を超えれば十分」と慰めてくれたそうだが、息子は自分の実力の無さに納得出来ない様子。
息子は今回の受講をW(停止)にして、次の学期か夏休みに再受講を狙いたいらしいが、私は「レベルが大きく違うのだから、同じ講義を受けても受け取り方が違ったり理解の深さも違うよな。再受講しても同じ成績じゃね?」と、実力不足を認めさせる方向で説得中。
同じ大学でもレベルに開きがあり、難関の学部と一緒の講義だと、合わせて相対評価されるので苦労するみたいだ。
息子へは「卒業できれば十分だから、頑張れー!!!」と言っている。w
さて久しぶりに先週出題した数学の解答。
前回の問題

式の値を求めなさい。
メンカームの解答
友達が通う塾の宿題だったそうで、教えを請われた娘が困って私へ連絡してきたが、このパターンの問題は一度やった事があっても解法を思い出せない。
私の返事が遅いので娘は自分で取り組み、分数の繰り返し部分(2ー1/…)が1なら辻褄が合うのに気付き、友達へ4だと答えたそうだが、択一式問題なら満点が貰えても、記述式だと部分点しか貰えない。
私が「分数の繰り返し」で検索すると『連分数』と言うのが判ったが、ウィキペディアの連分数のページを見ても私の頭ではさっぱり意味不明。YOUTUBEで動画を検索してようやく解り易い解説動画を見つけた。
【無限に続く2つの式】連分数と√1+√1+√1+…の計算
動画を参考に解いてみる。
下の式で赤く囲った部分をAとすると…

同じ分数の繰り返しなので、下の式で青く囲った部分もAと表せる。
すると上の式で赤く囲った部分は 2ー(1/A)=A となり、これを解くとA=1となる。

分数の繰り返し部分(2つ上の式で赤く囲った部分)をAとすると、与式は 7-(3/A) であり、A =1なので4となる。

答え 4
ムガさんところのお兄ちゃん、正解です。\(^o^)/
#連分数 #中学数学
タイの中学生向け数学ギフテッド問題の記事へのリンク→#高1入試ギフ
貴方のクリックとコメントが、このブログのパワーの源です。
下のバナーへ応援クリックをお願いします。
 海外生活ブログ タイ情報 人気ランキングはこちら
海外生活ブログ タイ情報 人気ランキングはこちらリアルタイムに更新される新着記事一覧(右下)からタイの今が見える。お薦め。

















