まったく、突然に数独です。７月１９日に「第４章 上級ステップ（とりあえずの終わりに）」を最後に、その後数独についてはまったく触れていません。その時は「どんな超難問数独でも解決出来る方法を解説します」とのタイトルのもと、３７回に亘る連続の解説を載せましたが、途中「全ての難問が解ける方法」には至っていないことに気が付き、「今後に待ちたい」として、”筆を折り”ました。
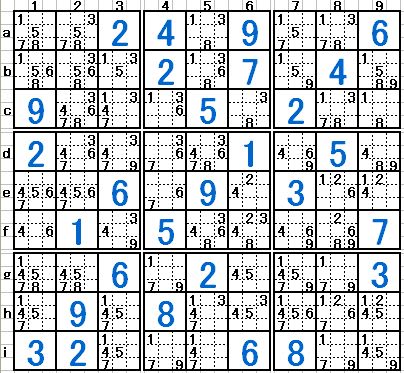
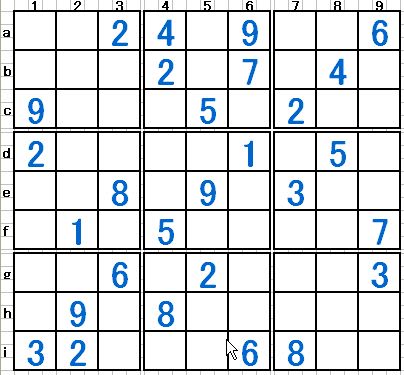
いまだ完全解決への道遥かに遠し、です。それどころかそんな姿勢をあざ笑うかの様な問題を紹介するメールが２本、同じ日に違う方から届きました。「解けたら天才！フィンランドの数学者が作った”世界一難しい数独”」とのタイトルのメールにはその紹介記事と、その数独の問題が書かれていました。右図がその問題です。解いてみてください、と言うより数独の現在の一断面の紹介の積もりで、最下段にその記事が書かれている URL を乗せました。数独のある断面が乗っていますから、宜しければお読みください。
その概略を書きますと
《海外の複数のニュースサイトが伝えるところによると、上記の問題は実はフィンランドの数学者 Arto Inkala 氏が作成した問題で、彼曰く”世界でもっとも難しい数独”とのこと。問題は彼が作成した問題作成プログラムによって作成したもので、問題作成にはなんと３ヶ月を要したそう。》で、問題解決には軽く数週間はかかるでしょうとまで書かれていました。マーちゃんも早速問題に取り組みましたが、確定数は僅か２個、あと手筋を用いて候補数を一つ消しただけで、まったく先が見えません。
日本発の「数独」というパズル、イギリスで大フィーバーし世界各国に広がりました。日本でも「ニコリ社」からは「激辛数独」などの問題集が、世界文化社からは「難問ナンプレ」と名付けられた問題集などが数多く発売されています。池田書店から発売された「極」の編著作はイスラエル人です。マーちゃんは日本作家の作品はその作風や使われる手筋を知るが故に多くの問題を解けますが、外国人作の問題は、苦戦が続いています。
http://headlines.yahoo.co.jp/hl?a=20100824-00000018-zdn_g-ent
（２）候補数を消去する
⑮その他の手筋
例えば「XYZ-wing」等まだまだ多くの手筋があります。ただマーちゃんはその辺の部分は未だ不勉強で、具体的題材の収集も出来ていません。「どんな超難問数独でも解決出来る方法を解説します」が看板倒れに終わりそうですが、ただ、今までの説明で現在市販されてい超難問は殆ど解決できると考えています。「二コリ社」の「激辛数独」も「世界文化社」の「難問ナンプレ」や「ナンプレ超上級編」も解決します。挑戦してみてください。
ここで紹介が出来ず、ミシチャンさんのホームページに登場するような手筋が問題に組み込まれていれば解けないこともあるかと思いますが、ご容赦下さい。それに新たに手筋が発見される事もあります。ナンプレ・数独の世界は日進月歩しています。いずれ又知識を整理してからこの続きを書き出したいと思いますが、今日でとりあえず終了します。
長らく読み続けられた方がいらっしゃいましたら心からお礼申し上げます。マーちゃんは、東京散歩とか、再度の百名山、江戸時代の数学（和算）などに興味があります。身辺雑記も含め、今後はそれらについてのブログを書きますので、宜しければそちらをお読み下さい。（７月２２日以降）
最後の幾つかはマーちゃんが気が付いた事柄です。図１をご覧下さい。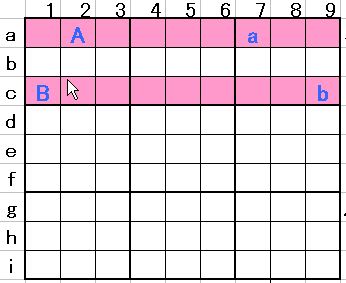
図１
「X-wing」が「候補数が二つのだけの行が２つあり、その候補数が同じ列の上にあるならば、その列にはその候補数はそれ以外には存在しない」と言うものでした。（行と列を入れ替える事可能）
この「X-wing」の手筋の後半部分を書き換えるとどうなるでしょう。
仮定は「候補数が二つだけの行が２つあり、その候補数が同じブロック内にあるならば・・・」です。どんな結論が待っているでしょうか？
候補数５についての配置が図１の様に、ａ行にはAとa、ｃ行にはBとｂとします。この時AとBが同じブロックに、aとbも同じブロックに属しているという仮定です。このときにも消去出来る候補数があります。図２を見て下さい。
図２
例えば図２で黄色印マスのどれかが５で確定したとすると、ａとｂは消去され、AとBが残りこれは困ります。（具体的事例を前提にしての話ではありませんので、この様な仮定がありえるのか否か検討していません。黄色印マスでの５の確定がAとBの存在に影響を与えない、とします）
謂わば「X-wing」の拡張は次の様にも言い換えられます。
図３
図３で「候補数が二つだけのブロックが２つあり、その候補数が同じ行の上にあるならば・・・」。さてこのときの結論はどうなるでしょう。図４を見てください。
図４
例えば黄色印マスのいずれかが５で確定すれば、ａ、ｂは消去され、ａ行にAとBが残ります。これは困ります。だから黄色印マスに５は存在し得ず、こから候補数５を消去出来ます。
図５からは「Sashimi Fish」や「Finned Fish」の拡張を考えますです。
ミシチャンさんのホームページを参考にさせていただきましたが、理屈はマーちゃん流です。図５を見て下さい。
図５
図５は「Sword Fish」が成立しています。その時黄色印マスに５は入りません。理屈を復習します。
もし黄色印マスに５が入ればａ’、ｂ’、ｃ’は消去され、Aa, Bb , Ccが残されます。この形覚えておくと有効だと思います。あってはならない配置なのです。（”困った配置”と呼ぶ事にします。仮にAa, Bbでの「X-wing」が成立と見立てればCcが消えてしまいｈ行に５は存在しえなくなってしまいます）これが「Sword Fish」で候補数を消去出きる理屈です。この理屈は次のような局面でも使えます。
図６
「Sashimi Fish」の「Sword Fish」版です。ｂ行、ｅ行、ｈ行に候補数は３個（２個でも可）で、候補数が上記の様に配置されているとします。このとき候補数５を消去出来るマスがあります。
図７
図７でａ’、ｂ’、ｃ’の３つを見る事の出来るマス、すなわち黄色印マスから候補数５を消去出来ます。（理由は、ここで５が成立すると、ａ’、ｂ’、ｃ’が消去され、”困った配置”となってしまいます。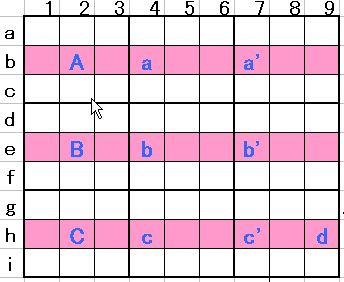
図８
図８は「Finned Fish」の「Sword Fish」版です。
図９
図９の黄色印マスから５が消去出来ます。
黄色印マスで５が確定すると、ａ’、ｂ’、ｃ’、ｄが消去され、Aa, Bb, Cc の”困った配置”になってしまうからです。
（２）候補数を消去する
⑭「Finned Fish」の成立を調べる。
図１は前回のブログでの提出問題です。
Fi
図１
図２は候補数の配置を明らかにしたものです。
マーちゃんはこの図を基にして、オセロ石を置いて１～９の順に「Finned Fish」と「Sashimi Fish」の成立を一気に調べます。
図２
図３
候補数８について、黄色印マス５個で「Finned Fish」が成立しています。そこでｃ６、ｃ８、ａ８の全てを見る事の出来るマスｃ９から候補数８が消去されます。その結果ｃ９＝１となり、図４に至ります。
図４
（２）候補数を消去する
⑭「Finned Fish」の成立を調べる
図１を見てください。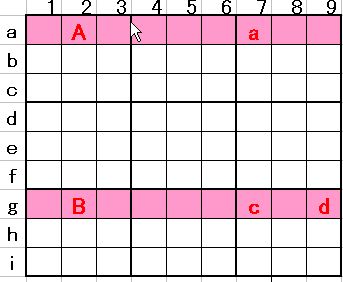
図１
図１も「Sashimi Fish」と同じように、「X-wing」が成立しそうで、僅かなところで「X-wing」は成立していません。「Sashimi Fish」が、候補数４個で成立した手筋に対して、上記の場合はｇ行の候補数が３個。この局面で消去出来そうな候補数は無い様に思えます。ところがあるのです。
先ず候補数の配置から説明します。「Sashimi Fish」のとき同様、候補数５について、以下の様になっているとします。
ａ行はAとaが対をなしています。
ｇ行に候補数は３個あり、それらの記号は、対をなすわけではないのでBに対してのbを用いないで、ｃ、ｄで表しています。ｄを取り去れば「X-wing」成立、言い方を変えれば「X-wing」にｄが追加されている配置です。この時,候補数５は消去出来るマスはあるでしょうか？暫く考えた後に図２をご覧下さい。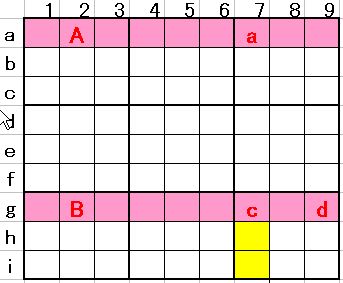
図２
上図の黄色印マスから候補数５を消去出来ます。理由は簡単です。この黄色印マスで５が成立すれば、ａ、ｃ、ｄは全て消去され、その結果AとBが成立する事になり、これは困ります。だから黄色印マスから候補数５を消去出来る分けです。
この一連の理屈を「Finned Fish」と呼ぶそうです。
finned を英和辞書で調べると、「ひれをもった」とか「ひれの・・」とあります。「X-wing」を魚に見立て、それにひれが付いたと言う意味でしょうか。或いは”ひれの付いた魚”と言う風に解釈すれば、このネイミングが理解可能です。
今後のブログで展開しようとする理屈を理解していただく観点を紹介すれば、ａ、ｃ、ｄの全てを見る事の出来る地点（＝マス）で候補数５は不成立です。AとBが残るような状況はあってはならないとの判断から、消去マスを見つけるわけです。例えば図３をご覧下さい。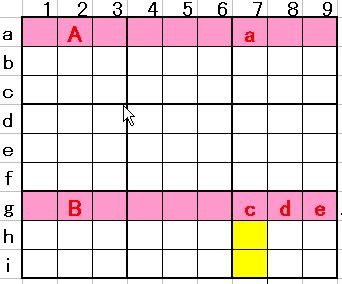
図３
図３は「Sashimi Fish」でも「Finned Fish」でもありません。敢えて言えば、ｄを取り去れば「Finned Fish」、ｃとｅを取り去れば「Sashimi Fish」で、「Finned Fish」＋「Sashimi fish」の様な状態です。「手筋」ではありませんが、このａ、ｃ、ｄ、ｅを見る事が出来るマスでは５は不成立のはずです。黄色印マスはこれらをすべて見渡せます。だから黄色印マスから５を消去出来ます。
この手筋発見でも２つのライン、ＡａラインとＡＢラインが直角をなす事の発見に神経を集中することで、この手筋発見が可能となると思います。 次のような観点からも発見への糸口が開けると思うのです。
それは対をなすラインＡａラインに平行で２個又は３個の点（＝マス）を持つラインの存在発見に精神を集中させる、と言う観点です。
例題 次の局面で「Finned Fish」を発見してください。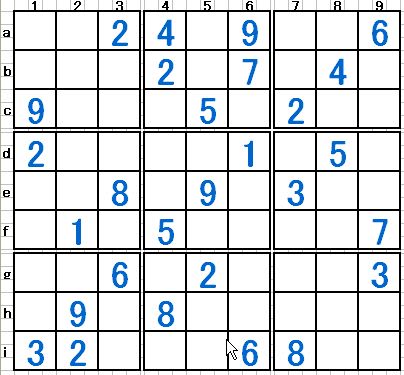
図４
解説は次回のブログで。
（２）候補数を消去する
⑬「Sashimi Fish」の成立を調べる
それにしてもこの手筋に妙な名前をつけたものです。多くの手筋に「Fish」が付けられる理由、面白いと思いますが、私には謎です。一体誰がいつ頃、これらの手筋を発見したのか興味が湧きます。外国の文献を読めば少しは様子が分かるかもしれませんが・・・。図１は前回のブログでの問題の再掲です。
図１
候補数の状況を明らかにして図２です。
図２
マーちゃんは１～９の順にオセロ石を配置して調べます。
そのときに、”対をなす”二つのマス、云わば２点を結ぶ線分が２本あり、直角をなす場合を捜すのに精神を集中させます。
候補数７の配置がその様になっていました。図３を見てください。
図３
”対をなす”マスを結ぶ線分は、ｅ３ーｅ４ ラインが一本、ｅ４－h４ のラインがもう一本、この２本が直角を形成しています。
黄色印マス４個が「Sashimi Fish」形成です。このときマスｈ４とマスｉ３の両方を見るマスｈ１（水色印マス）から７が消去出来ます。ｈ１＝７が成立すれば、ｉ３≠７、ｈ４≠７。だからｅ３＝７かつｅ４＝７ が成立して困ります。∴ｈ１＝５ です。
ペア数｛５７｝の奇数個の連鎖 ｈ１－ｉ３－ｅ３ で「浜田ロジック」が成立しｈ１＝５、ｉ３＝７、ｅ３＝５ と解く事も出来ます。
その後は問題なく図４の最終局面に到達です。
図４