サーブやトスのボールの軌道を電卓で求める

http://sports.blogmura.com/volley/

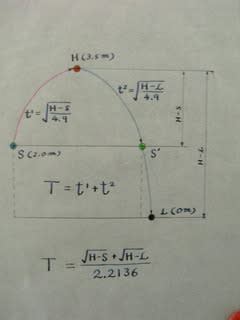
結論から言いますと、ボールが放り出される時の床からの高さＳ，放物線の頂点の高さＨ，ボールが到達する場所の高さＬ、その移動に必要な時間Ｔ（秒）の関係は一番下の式になるってことなんですね。

この式によって、時間差攻撃やゼロクイックパスからのフェイクトスのときのセミクイックのトスの高さを計算できるのです。特に自分たちよりも身長の高い選手と試合するとき、ブロックが飛ぶ前か、落ちた瞬間にスパイクを打つ必要が生じてきますでしょ？この戦術が有効なのです。サーブの軌道と到達時間を求めて、レシーバーの守備能力（移動距離と時間）に応じたフォーメーションを考えたり、自分にぴったりの後衛のサーブレシーブ位置（２０度原則）を探すのにも役立ちます。 

もちろん、いくら計算しても演ずるのが人間ですから、計算どおりいかない部分はありますが、選手に指導する上での理論を理解させるのには最適で、打ちやすいトスを思い切って真下に叩きつけるようなスパイクばかりを練習するアタッカーには、チーム戦術を考える場合このことをまず、理解させるようにしています。私は、かなり使って実績を残せたのでここに紹介しておきますね。

では式の説明です。

Ｓ、Ｈ、Ｌ、Ｔのいずれか一つの数値がわからなくても、残りの数値が判明していれば、この式に当てはめて求めることができます。

電卓を使って計算するときの方法を例示しておきますね。

 

１　頂点の高さＨから、ボールが出される高さＳを引きます。

　　仮に図のとおりＨが３．５ｍでＳが２．０ｍであるなら

　　３．５ｍ－２．０ｍ＝１．５ｍ

　　となります。

 

２　上記１で数値が出てきたら電卓の「√」ボタンを押し、平方根を
   求めます。

　　 例題でいきますと１．５の平方根が出て「１．２２4７・・・」
   という数値が出てきます。

 

３　次に頂点の高さＨからボールが到達する高さＬを引きます。

　　例題でいきますと

　　３．５ｍ－０ｍ＝３．５ｍ

　　ということになります。

 

４　上記３の式で数値が出てきたら電卓の「√」ボタンを押し、平方
  根を求めます。

　　例題でいきますと３．５の平方根が出て「１．８７０８・・」
  という数値が出てきます。

 

５　上記２と４の式で求められた数値を足します。
　　
　　例題でいくと、小数点５ケタ以下を四捨五入して

　　　１．２２４７＋１．８７０８＝３．０９５５

　　となります。

 

６　５で出てきた数値を２．２１３６で割ります。これが、Ｓから放　　
　　り出されたボールが放物線の頂点Ｈに達した後、Ｌまで落ちるの
　　に要する時間なのです。

　　例題でいきますと

　　３．０９５５÷２．２１３６＝１．３９８４秒

　　ということになります。

 

以上です。もちろん、Ｌがもっと上の場合でもできますよ。例えば床上０．５ｍという場合や、最大Ｈと同じ数値ってのもありますね。これらの計算も可能です。

この式を使いこなすと何秒後にある個所にボールを到達させるにはどのくらいの高さのボールを繰り出せばいいか？・・ってなことも分かってきます。

 

 

http://sports.blogmura.com/