学部3年生の無機材料科学Iの講義中に黒板の絵が下手で理解できなかった学生諸君に贈ります。
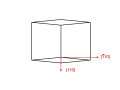
立方格子の3次元的構造図です。[100]と原点をはさみ逆方向に[-100]があります。

[100]と[010]のなす角が90°ですが、その間の45°の角度で原点から手前に伸びる方向が[110]です。つまり[100]と[010]をベクトルに見立てれば、その足し算といえます。そうであれば、[-100]と[010]の足し算は[-110]になりますね。

よって、[110]方向から立方格子を見れば、右に伸びるのは[-110]ということです。
もうひとつ。今日教えきれなかった内容です。
ひとつの種類の原子が並ぶなら、X線回折で禁制回折となってしまうのは、d2の間隔です。
● ● ● ● ● ↑
● ● ● ● |d2
● ● ● ● ● ↓
ところが真ん中の列が異なる原子(あるいはイオン)の列だったらどうでしょうか?X線の反射係数が原子によって異なるので、反射X線同士が相殺されません。この場合d2に関する回折線は弱いながらも得られます。
● ● ● ● ● ↑
○ ○ ○ ○ |d2
● ● ● ● ● ↓
CsCl構造が下の図に対応します。bccならd2は禁制回折なのに、CsClではd2は禁制にならない。ということは、CsClはbccではないことになります。sc(単純立方格子)なら、すべての回折が現れます。禁制回折はありません。下の図のCsCl構造はscです。
立方格子の3次元的構造図です。[100]と原点をはさみ逆方向に[-100]があります。

[100]と[010]のなす角が90°ですが、その間の45°の角度で原点から手前に伸びる方向が[110]です。つまり[100]と[010]をベクトルに見立てれば、その足し算といえます。そうであれば、[-100]と[010]の足し算は[-110]になりますね。

よって、[110]方向から立方格子を見れば、右に伸びるのは[-110]ということです。

もうひとつ。今日教えきれなかった内容です。
ひとつの種類の原子が並ぶなら、X線回折で禁制回折となってしまうのは、d2の間隔です。
● ● ● ● ● ↑
● ● ● ● |d2
● ● ● ● ● ↓
ところが真ん中の列が異なる原子(あるいはイオン)の列だったらどうでしょうか?X線の反射係数が原子によって異なるので、反射X線同士が相殺されません。この場合d2に関する回折線は弱いながらも得られます。
● ● ● ● ● ↑
○ ○ ○ ○ |d2
● ● ● ● ● ↓
CsCl構造が下の図に対応します。bccならd2は禁制回折なのに、CsClではd2は禁制にならない。ということは、CsClはbccではないことになります。sc(単純立方格子)なら、すべての回折が現れます。禁制回折はありません。下の図のCsCl構造はscです。



















