(2)候補数を消す手筋
⑥「X-wing」を捜す
さて、いよいよ「X-wing」です。数独の解法についての説明を読んだ事があれば、一度はこの「X-wing」の説明に接した事があると思いますが、改めて「X-wing」に述べます。下図1をご覧下さい。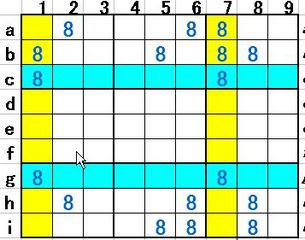
図1
図1は候補数8の配置を記録したものです。その特徴はc行とg行(水色のライン)には候補数8が2個だけ登場しています。しかもc行の8もg行の8も、共に1列と7列に存在しています。
この時、1列上と8列上(黄色のマス)には8は存在し得ない、言い方を変えれば、8を消去出来るのでした。その結果図2の局面に変化します。
図2
その理由を図3で説明します。
図3
今ある候補数(例えば8)の配置が図3の如くであったとします。詳しく書くと、候補数8はc行のマスAとBに存在し、かつg行のマスCとDに存在していて、青いライン以外では8を省略していいます。
この時 仮にA=8 ならば B≠8であり、その結果
かつC≠8 だから D=8
逆にA≠8 ならば B=8であり、その結果
D≠8 だから C=8です。
つづめて言えば『AとDが8』または『BとCが8』が成立しています。どちらが成立してもc行・g行・1列・7列にはA・B・C・Dマス以外に8は存在しえません。c行とg行には候補数は2個と言う前提でしたから、ここ以外に8は存在しないのは当然として、1列と8列に8は存在しないと言う新たな事実が現れ、その結果として黄色マスに存在する8は消されます。
この『AとD』並びに『CとD』を線分で結ぶと文字『X』の様になる事から「X-wing」と呼んだのだと思います。
ただ注意する点はA・B・C・Dの4マスが共に同一のブロックに属するときは「X-wing」の手筋は使えないと言うことです。
「X-wing」の理屈はそれほど難しいものではありませんが、問題を解く実戦の場で「X-wing」を見出すのはそれほど容易いではありません。
例題1で考えて下さい。問題はこの局面で「X-wing」を見出し、消去すべき数があれば消去しなさい、です。
例題1 ある数独の問題を解いていって、手筋を使い次の局面 に達しました。さて「X-wing」は何処にあるでしょうか?
解答 下の図の黄色いマスの候補数3が「X-wing」です。i2とi6(ピンクの数3)が消去されます。
3を消去して下の図に至ります。









