今日の１問目は、難問が多いと言われるシリントーン試験の小学生向け過去問題から、私が最後まで悩んだ設問を紹介。
１６ ２０ Ａ の最小公倍数は１２００。
Ａに成ることが出来る全ての数の和を答えなさい。
最小公倍数（さいしょうこうばいすう、英: least common multiple）とは、０ではない複数の整数の公倍数のうち最小の自然数をさす。たびたび、L.C.M.等の省略形で記述される。（ウィキペディア 最小公倍数より）タイ語ではコロノーだ。すだれ算で最小公倍数は求めても、機械的にやるだけなので、このような問題で悩んでしまう。
今回の問題は正解が入手できず、勉強嫌いで算数は特に苦手な私が解いているので、間違えている可能性がある。気付かれた方はぜひ指摘して欲しい。
先ずは、１６と２０の最小公倍数を調べる。
１６と２０の最小公倍数は、２4×５＝８０と判る。
１６と２０とＡの最小公倍数は１２００なので、１２００÷８０＝１５＝３×５であり、
すだれ算は、上の様に ２4×５2×３ となる。
下から１５×５＝７５ ７５×２＝１５０ １５０×２＝３００ ３００×２＝６００ ６００×２＝１２００と計算すれば、Ａ＝１２００と求められる。
「おい、出来たぞ！」と娘へ見せると、「Ａに成ることが出来る全ての数の和って書いてあるじゃない！」と叱られてしまった。
「え？どういう仕組？」と、しばらくすだれ算とにらめっこする私。勉強嫌いなだけに基礎からなってないので分らない。（恥ｗ）
１６と２０とＡの最小公倍数なので、一番下が３×５＝１５なのは間違い無いが、Ａ＝１５にしようとしても・・
１５は５で割れる数なので不可能。
１５×５＝７５ ５2×３＝７５の部分は確定。
７５は２で割れないので・・
Ａ＝７５は可能。
すだれ算の最初だけ２で割ると、
Ａ＝７５×２＝１５０。
すだれ算の最初と２段目を２で割ると、
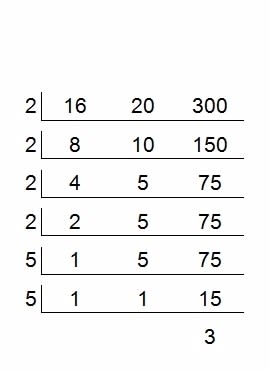
Ａ＝７５×２×２＝３００
すだれ算の最初と２段目と３段目を２で割ると、
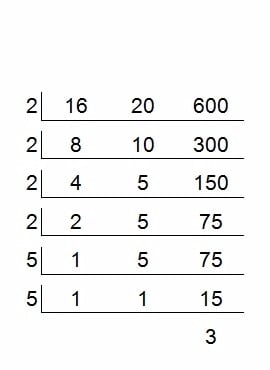
Ａ＝７５×２×２×２＝６００
すだれ算の最初から４段を２で割ると、
Ａ＝７５×２×２×２×２＝１２００
Ａに成ることが出来る全ての数は７５，１５０，３００，６００，１２００であり、その和は２３２５。
２問目は
から階乗の問題。階乗は「（その３）タイの小学生向けの模試等へ出題される、解答パターンを知らないと解けない計算問題はこれ。」で一度紹介したが、覚えておられるだろうか？
数学において非負整数 n の階乗（かいじょう、英: factorial）n ! は、1 から n までのすべての整数の積である。例えば、6!=6×5×4×3×2×1=720である。空積の規約のもと 0! = 1 と定義する。 Wikipedia 階乗より引用。
それでは問題。
（５０！－４９！－４８！）÷（５０！＋４９！＋４８！）の値を求めなさい。
５０！＝５０×４９×４８×４７×・・・×２×１
４９！＝４９×４８×４７×・・・×２×１
４８！＝４８×４７×・・・×２×１
５０×４９×４８×４７×・・・×２×１－４９×４８×４７×・・・×２×１－４８×４７×・・・×２×１なんて計算できないのに、設問を書いたホワイトボードをじっと眺めている娘。私は未だ覚えていたが、娘は完全に忘れている。(ﾉД`)ｼｸｼｸ
ヒントを書くと・・
５０！＝５０×４９×４８！ ４９！＝４９×４８！ 娘はこれを忘れてる。
それでは解答
５０！－４９！－４８！
＝５０×４９×４８！－４９×４８！－４８！
＝４８！（５０×４９－４９－１）
＝４８！（５０×４９－５０）
＝４８！（５０（４９－１））
＝４８！（５０×４８）
＝４８！×２４００
５０！＋４９！＋４８！
＝５０×４９×４８！＋４９×４８！＋４８！
＝４８！（５０×４９＋４９＋１）
＝４８！（５０×４９＋５０）
＝４８！（５０（４９＋１））
＝４８！（５０×５０）
＝４８！×２５００
（５０！－４９！－４８！）÷（５０！＋４９！＋４８！）
＝（４８！×２４００）÷（４８！×２５００）
＝（４８！×２４００）／（４８！×２５００）
分母と分子を４８！×１００で割って
＝２４／２５
ＵＰ校の理数特別クラスを受験する娘の入試対策に、中３レベルの文章題の問題集
を解かせていたが、「高校の数学教員室へ入っても入試問題を作っている雰囲気ではないので、中学の入試問題も外部の筈」とＵＰ校へ通う息子が言うので、昨年同様に外部で入試問題が作成されて難問は出ないと見て、中学受験レベルの算数ギフテッド問題集 へ変更。
少し複雑な数列の和や大きな数字の約数の数を求めたりは、最近やってなかったので怪しい。クリスマス前に終わらせるつもり。
タイの小学生向け算数ギフテッド問題の記事へのリンク→#中１入試ギフ
貴方のクリックとコメントが、このブログのパワーの源です。
下の２つのバナーへ応援クリックをお願いします。
海外生活ブログ タイ情報 人気ランキングはこちら
リアルタイムに更新される新着記事一覧（右下）からタイの今が見える。お薦め。
タイの人気ブログが大集合！！
登録数 アクセス数 最大級のブログランキング
ブログの世界が広がります。
１６ ２０ Ａ の最小公倍数は１２００。
Ａに成ることが出来る全ての数の和を答えなさい。
最小公倍数（さいしょうこうばいすう、英: least common multiple）とは、０ではない複数の整数の公倍数のうち最小の自然数をさす。たびたび、L.C.M.等の省略形で記述される。（ウィキペディア 最小公倍数より）タイ語ではコロノーだ。すだれ算で最小公倍数は求めても、機械的にやるだけなので、このような問題で悩んでしまう。
今回の問題は正解が入手できず、勉強嫌いで算数は特に苦手な私が解いているので、間違えている可能性がある。気付かれた方はぜひ指摘して欲しい。
先ずは、１６と２０の最小公倍数を調べる。
１６と２０の最小公倍数は、２4×５＝８０と判る。
１６と２０とＡの最小公倍数は１２００なので、１２００÷８０＝１５＝３×５であり、
すだれ算は、上の様に ２4×５2×３ となる。
下から１５×５＝７５ ７５×２＝１５０ １５０×２＝３００ ３００×２＝６００ ６００×２＝１２００と計算すれば、Ａ＝１２００と求められる。
「おい、出来たぞ！」と娘へ見せると、「Ａに成ることが出来る全ての数の和って書いてあるじゃない！」と叱られてしまった。
「え？どういう仕組？」と、しばらくすだれ算とにらめっこする私。勉強嫌いなだけに基礎からなってないので分らない。（恥ｗ）
１６と２０とＡの最小公倍数なので、一番下が３×５＝１５なのは間違い無いが、Ａ＝１５にしようとしても・・
１５は５で割れる数なので不可能。
１５×５＝７５ ５2×３＝７５の部分は確定。
７５は２で割れないので・・
Ａ＝７５は可能。
すだれ算の最初だけ２で割ると、
Ａ＝７５×２＝１５０。
すだれ算の最初と２段目を２で割ると、
Ａ＝７５×２×２＝３００
すだれ算の最初と２段目と３段目を２で割ると、
Ａ＝７５×２×２×２＝６００
すだれ算の最初から４段を２で割ると、
Ａ＝７５×２×２×２×２＝１２００
Ａに成ることが出来る全ての数は７５，１５０，３００，６００，１２００であり、その和は２３２５。
２問目は
から階乗の問題。階乗は「（その３）タイの小学生向けの模試等へ出題される、解答パターンを知らないと解けない計算問題はこれ。」で一度紹介したが、覚えておられるだろうか？数学において非負整数 n の階乗（かいじょう、英: factorial）n ! は、1 から n までのすべての整数の積である。例えば、6!=6×5×4×3×2×1=720である。空積の規約のもと 0! = 1 と定義する。 Wikipedia 階乗より引用。
それでは問題。
（５０！－４９！－４８！）÷（５０！＋４９！＋４８！）の値を求めなさい。
５０！＝５０×４９×４８×４７×・・・×２×１
４９！＝４９×４８×４７×・・・×２×１
４８！＝４８×４７×・・・×２×１
５０×４９×４８×４７×・・・×２×１－４９×４８×４７×・・・×２×１－４８×４７×・・・×２×１なんて計算できないのに、設問を書いたホワイトボードをじっと眺めている娘。私は未だ覚えていたが、娘は完全に忘れている。(ﾉД`)ｼｸｼｸ
ヒントを書くと・・
５０！＝５０×４９×４８！ ４９！＝４９×４８！ 娘はこれを忘れてる。
それでは解答
５０！－４９！－４８！
＝５０×４９×４８！－４９×４８！－４８！
＝４８！（５０×４９－４９－１）
＝４８！（５０×４９－５０）
＝４８！（５０（４９－１））
＝４８！（５０×４８）
＝４８！×２４００
５０！＋４９！＋４８！
＝５０×４９×４８！＋４９×４８！＋４８！
＝４８！（５０×４９＋４９＋１）
＝４８！（５０×４９＋５０）
＝４８！（５０（４９＋１））
＝４８！（５０×５０）
＝４８！×２５００
（５０！－４９！－４８！）÷（５０！＋４９！＋４８！）
＝（４８！×２４００）÷（４８！×２５００）
＝（４８！×２４００）／（４８！×２５００）
分母と分子を４８！×１００で割って
＝２４／２５
ＵＰ校の理数特別クラスを受験する娘の入試対策に、中３レベルの文章題の問題集
を解かせていたが、「高校の数学教員室へ入っても入試問題を作っている雰囲気ではないので、中学の入試問題も外部の筈」とＵＰ校へ通う息子が言うので、昨年同様に外部で入試問題が作成されて難問は出ないと見て、中学受験レベルの算数ギフテッド問題集 へ変更。少し複雑な数列の和や大きな数字の約数の数を求めたりは、最近やってなかったので怪しい。クリスマス前に終わらせるつもり。
タイの小学生向け算数ギフテッド問題の記事へのリンク→#中１入試ギフ
貴方のクリックとコメントが、このブログのパワーの源です。
下の２つのバナーへ応援クリックをお願いします。
海外生活ブログ タイ情報 人気ランキングはこちらリアルタイムに更新される新着記事一覧（右下）からタイの今が見える。お薦め。
タイの人気ブログが大集合！！登録数 アクセス数 最大級のブログランキング
ブログの世界が広がります。
今の自分にはスーパーのレジ以外の計算には縁がない（笑い）
熾烈な戦いの火中って事ですね。
日本もその他の国も、大変なのが、何となく理解できました。
目標に受かりますように～～♪
下手なバカコメントで足を引っ張るのは受験後に延ばさせていただきます(^-^;
えーと、うちの娘はクリスマスプレゼントは初音ミクのコスプレセットがいいとか言ってる段階で、焦る気も失せました(-_-;)
おっと、その先輩の6年生ですが、Ｙ校に9人、私立Ｐ校には3人合格してますが、大学附属Ｓ校には一人だけと昨年よりも厳しい結果ですね。今は来年行われる理数科、英語科、普通科へ向けて追い込みの時期でしょう。
お嬢ちゃんはそれより数段上の闘いです。寒くなりましたので体調に気をつけて頑張ってください。p(･∩･)qｶﾞﾝﾊﾞﾚ!
普段の生活で公倍数や階乗を使いませんから、
歯が立たないのが普通ですね。
私も最初は子供達から算数を教えてくれと言われ、
全然解けませんから困ってました。
日本から買った参考書無しでは難しいです。
入試を目前にして熾烈な戦いが続いており、
塾を待っている間の父兄の井戸端会議はＵＰ校１組へ誰が入るか。
合格順位の予想まで出来上がってます。
そして１組を予想された子供や親同士のネットワークが既に作られ、
あれだけ秘密だった塾の情報がドンドン入り、
直前対策を一緒の塾でやろうとお誘いまで。
昨日はバンコクで模試があり、うちは行きませんが、
ウドンを代表する面々が行かれて得点は即日発表。
井戸端ランキングの正確さに驚きました。
応援ありがとうございます。
mugaさん
階乗はやり方だけ知っていればパターンですが、
コロノー・ホロモーは簡単そうに見えて奥が深いです。
昨日も問題集が解けなくて解答を見ても分らない。
その内に解答に矛盾を見つけてｗｗｗ。
本を書くような先生も間違えている。
受験生が二人の我家では、塾のプレゼント交換の話はあっても
そこで終わってます。（寂）
昨日はバンコクで模試がありました。
うちは行きませんが、ウドンを代表する面々がチャレンジ。
五年生の頃までは抜群の強さを発揮していた子が没落し、
無印だった子がぐんと伸びたりで、ここでも下克上。
ウドンタニで１位と５位のこの得点差が５０点満点で１７点ですよ。
娘は毎日頑張ってますが、ここを駆け上がるのは至難の業です。
ただしこの５人の勉強法はご父兄から直接伺いまして、
１７点の違いが出る理由はなんとなく理解できました。
また記事にします。
応援ありがとうございます。
１２００を素数分解します ２の４乗かける
３かける ５の２乗 これが最小公倍数という事は
１６は２の４乗、２０は２の２乗かける５．
公倍数は ２は４乗 、３は１乗 ５は２乗 でできています。 したがって Aは３かける ５の２乗が一番小さい数です。あとは Aになれるのは ２倍 ４倍 ８倍 １６倍 の数です。これは１６が２の４乗だからです。
Aになれる数字の和は
７５かける （１+２+４+８+１６）＝31
2325
良かったメンカームさんと同じ答えです。まあ
５5年ぶりで最小公倍数なんか忘れていました。
半分 勘と あとだし、じゃんけんですね。
最小公倍数とは 素数 の飽和の問題であるとの
勘がよみがえったものです。問題を考えた今は
だいぶ勘が戻っています。
最小公倍数というのは 各数字を素数分解して
、各数字の素数の乗数の一番大きいもの同士を掛けたものになると思います。たぶん。
息子さんの合格をお祈りします。
A , B, C の最小公倍数は Dである。
A 、B C, になりうる 数字で
一番大きな数字を答えなさい。
答え D
ところで素数分解という言葉は、適当に書きました。
正しくは素因数分解でした。
こんな言葉も忘れていました。
これが小学生の問題とは大変ですね。
最小公倍数とは
かく数字を 素因数分解して、
素数の積で書き、、 異なる素数の乗数の一番
大きい素数たちの積がさしよう公倍数という感じですね。勘。
階乗の問題も面白いですね。
要するに 同じ数字の組み合わせは一つの文字で
書けばよいですね。 ５０！は５０ｘ４９ｘ４８！ ５０ｘ４９ｘAとかという風に。
しかし高所から全体を見るというのは 小学生には
なかなむずかしいですよね。
小学生は 毎日社会で生きるというだけでも大変です。初めて経験することが多いので、つい目先のことに心を奪われます。当たり前です、経験が足らないのですから。
もう こおいうのは ゲームと思って 解くしかないですね。 とにかく最初はあんまり計算
はせずに 、同じものは、まとめてまとめて括弧でくくって計算して、最後までややこしい計算などは絶対にしないで、
分子分母の数字を食い合いさせてチャラというパターンですね。
５０！＝５０ｘ４９ｘ４８！を３回ほど経験すれば４回目からは忘れないでしょう。
がんばれ少女。
メンカームさんと同じやり方ですが、
目的地までの距離を ｌとする。
平均時速を a
とする。往復に要した時間は
２ｌ÷ a= ｌ÷４０ ⁺ｌ÷ ６０
右辺は５ｌ÷１２０
２ｌ÷ a＝５ｌ÷１２０
５la=240l
a=48
大昔 自分も 最初は、 そら、平均時速は５０ｋｍだとおもいました。
山あり 谷ありの人生を生きた人は（ものすごく良いときもあったが、ものすごく悪いときもあった） 、普通に生きた人よりも 平均時速は遅くなります。効率は悪くなります。
それだけ疲れるという事です。
しかし、それが真の男の人生というものです。
小学生ですから、本人はパターン通りにやって終わりにしたいでしょうが、
１問目は本質的な理解を求めた設問だと思いました。
２問目はパターンでして、やり方を知っていれば解けるかな？
最後までややこしい計算などは絶対にしなければ楽に解けるのですが、
娘は計算に自信があるからか、全部直ぐにやってしまおうとします。
πの問題も、πの計算は最後と何度も教えるのにやってしまう。
塾は半個別なんですが、先生が忙しいからか、式の建て方は教えても、
細かいところまではチェックが入ってないようです。
こうなると私が教えるしかありませんが、数学が苦手な人が教えても・・（恥ｗ）。
taiyaiさんから頂いているアドバイスが大変役立ってます。
私の今までの人生は、あまり良いとは言い難い環境でしたが、
幸いにもやりたい事は一通りやっている様な気がします。
今は子供の夢を叶える時。子供の夢が私の夢です。
娘が独り立ちするまで１２年は特に頑張ります。
それが済めば、また我儘いっぱい。好き放題にやりたいと思ってます。