量子現象の確率は何の属性か？

古典物理学は、現在の状態から過去未来の状態を決定するニュートンの運動方程式に基づいています。

気体や液体などを構成する個々の分子の状態もこの法則で表される。<BR>
しかし、１c.c.あたり10の１９乗個オーダーという膨大な数の分子集団の振る舞いを扱う場合、個々の分子の状態をすべて正確に記述することは不可能です。

そこで、熱統計力学では止むなく統計的手法を用いますが、それでも多くの法則が成り立つのです。

しかし、古典物理学では確率が本質的役割を果たすことはありません。
古典物理学で確率が使われる理由は、人間の知識不足によるものです。

一方、量子力学は量子現象にはもともと確率的性格があるとします。
アインシュタインは、ボルンへの手紙の中で「神はサイコロを振らない」という有名な言葉でこの主張に反対しました。

アインシュタインは、放射性元素の崩壊や原子における電子の遷移は偶然に起きると考えました。
これは、人間の知識不足による止むを得ないものでした。
この考えが隠れた変数の理論という概念につながるのです。

ところで、量子現象のような奇妙な現象に対して従来の確率概念を適用できるのでしょうか？
この疑問に対して次のような見方を提案します：
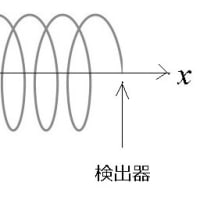
量子現象に関する確率は量子だけの属性ではなく、「量子」「現象を起こす装置（スリット、偏光板）」「検出器」からなるシステム全体の属性である。
量子現象の確率は、これらの協調によって初めて定義できるからです。

確率を計算する際にはデータの分類が必要です。
分類の仕方は、観測者が決めるものです。
ここに主観的な影響が生じます。

従って、量子現象に関する確率は絶対的、客観的な量ではありません。

量子現象に特有な確率を扱う「量子確率論」があります：
（１）二重スリット実験で片方のスリットのみを開けたときの結果を合わせたものと
（２）二つのスリットを同時に開けた結果とが一致しない

「干渉効果」を確率論として説明するために考案されたものです。

（大矢雅則ほか編　『数理情報科学事典』、pp.1059-1063、朝倉書店(1997)）

量子確率論における確率は、対象とする現象の属性である点では通常の確率論と同じです。

量子がジグザク運動していると仮定し、それを確率過程で表すことによってシュレーディンガー方程式と等価な方程式を導く研究もあります：
長澤正雄　『シュレーディンガーのジレンマと夢　－確率過程と波動力学－』、

森北出版(2003)）

詳細は、パソコンサイト　情報とは何か　情報と物質の関係から見える世界像　を是非ご覧ください！