09月07日 国立科学博物館の振子

09月07日 Fig1

そうそう、大昔を思い出しながら計算しているので間違っている可能性大です。違っていたらごめんなさいです。こんなことを考えた。

テレビで国立科学博物館の紹介をやっていました。そう言えば、あそこにはフーコーの振り子があったなぁ。ゆっくりと動くんだけれど何秒かかったかな。たしか高校で単純なものは習ったような。計算できるかなぁ。

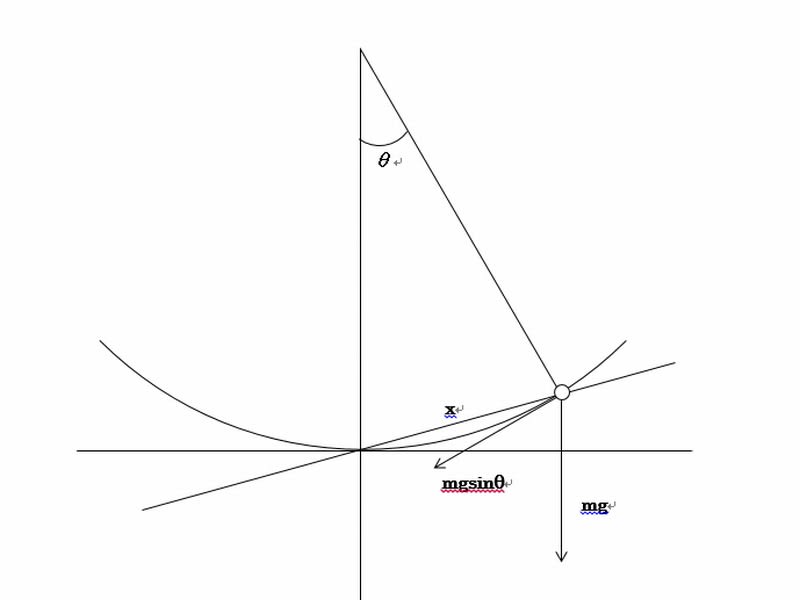
これsinθ≒θを使いたいので微小振動ってのを思い出しました。錘がスーッと下がっていくのでmgsinθが単振子の復元力F。sinθ = x/lなので F = -mgsinθ = -mgx/l。
おもりの円弧方向の加速度を a とすると、運動方程式はma = F = -mgx/l。 a = - gx/l
角振動数を ω (rad/s) とすると、単振動の加速度の式は a = - ω2x
この2つを比較すると - gx/l=- ω2x
変形して、ω = SQRT(g/l)
周期を T (s) とすると　T = 2π/ω　であるから、T = 2πSQRT(l/g)

あー面倒くさい。たしかこんな計算になったような気がします。

09月07日 エクセル

これをエクセルで計算させましょう。今回は単位が m (メートル)で計算しているのでそのまま使えるかな。

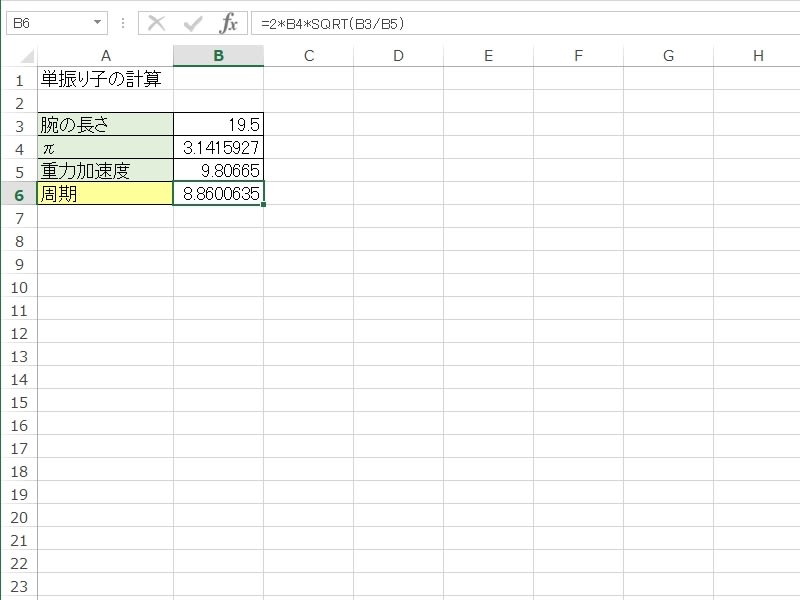
一例なのですが、セルb3には計算する長さ。セルb4はパイ(3.141592・・・)。セルb5には重力加速度。セルb6が計算結果。この例だと『=2*B4*SQRT(B3/B5)』こんな感じ。で、インターネットで国立科学博物館のフーコーの振り子の長さを調べると19.5m。では、b3に19.5を入力すると8.8600635と表示されます。約9秒で動いている計算になるようです。振り子で9秒ちかくかかるって凄いなぁ。

あー、やっと計算終わった。間違っていたらごめんなさいです。

こんなことやっているから
寝る時間なくなるんでしょうね。