中学生の時に読んだ学習雑誌にピタゴラスが三平方の定理を発見した時の逸話が載ってました。
エジプトでは辺の比が3・4・5で直角を作っていた。
そして別なところ(場所は忘れました)では5・12・13で直角を作っていた。
ピタゴラスはこの二つの三角形を視て三平方の定理を発見した。
逸話ですから本当のところは???ですが。
3・4・5 / 5・12・13 が直角三角形になることをこの時に知りました。
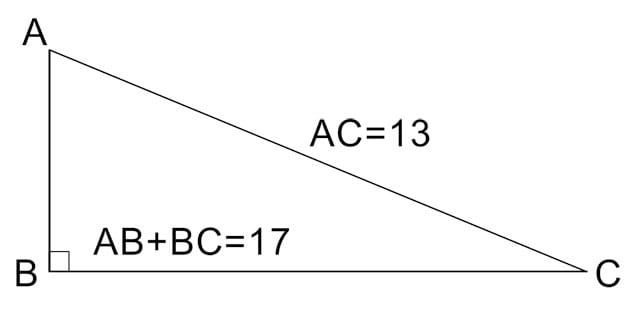
設問は斜辺が13であることから他の二辺は 5・12 であることは容易に想像がつきました。
5x12÷2=30 30㎠ 暗算で即答できました。
以下はネット(動画)での解説です。

補助線を用いて三角形ABCと合同な三角形※を図のように配置いたします。
三角形ABCと三角形CDEは合同~ AB=CD 故にBD=17
角◎+△=90° したがって 角ACEは90°
外側は一辺17の正方形 内側は一辺13の正方形
(17x17ー13x13)÷ 4 = 30
と、まあこんな解説でした。
さらに三辺をそれぞれx・y・zとして
z²=x²+y² と x+y=17 を連立に解いて
x=17-y
169=(17-y)²+ y²
169=289-34y+2y²
2y²-34y+120=0
y²-17y+60=(y-12)(y-5)
y= 5 ・12
中学校の入試ではちょっと疑問ですが。
ピタゴラス数
3:4:5 ・ 5:12:13 の他に
中学生の時には知らなかった 8:15:17 ・ 7:24:25
このほかにまだまだあります。



















