「バーゼル問題」について

　最近読み出した和算についての一冊に『江戸の数学教科書』(著:桜井進　出版:集英社)がある。第1章で江戸時代に和算がフィーバーした様子が語られ、第2章で円周率を求めようと奮闘した和算家たちの挑戦の様子が語られている。その中で「バーゼル問題」が紹介されていた。
　「バーゼル問題」など初めて目にする御仁も多いことと思う。数学アレルギーの方には見たくもない数式が登場するかも知れないが、ここで私が紹介したいこと、えっ！ということが4つほどあり、それをご覧頂きたいので最後までお付き合い願えればと思う。




　えっ！(1) 「バーゼル問題」とは右に掲げてある“自然数の平方の逆数の和”の値を求めよという問題で、式の後半に「・・・」とあるのは、無限に足すという意味だ。スイスの数学者ヤコブ・ベルヌーイはその値が確定することを証明したが、値を求めることは意外に難問で、解答を得られずに1705年に死去してしまった。ベルヌーイが暮らしていたスイスの都市バーゼルの名から「バーゼル問題」と呼ばれ、多くの数学者がその値を求めようとしてきた。

　この問題を解決したのがオイラーで1735年のことだった。右がその最終解答で、その式をご覧いただこう。左辺に登場するのは自然数だけなのにその無限個の和の結果の右辺にΠ(円周率パイ)という超越数という数が登場する意外性。オイラー自身がその結果に驚いたと伝えられている。これがえっ！(1)だ。

　えっ! (2)実はこの問題、オイラーの発見より13年前の1722年に和算家建部賢弘が解決していた。彼は、和算を知らない人でも聞いたことのある関孝和の高弟の一人。色々な業績があるが、円周率を小数点以下41桁まで算出していたことでも知られている。ヨーロッパ先んじて江戸中期の享保年間に日本で解決されていた。えっ！(2)だ。

　えっ！(3)時代は一挙に現代に飛ぶ。「バーゼル問題」の証明はいろいろあり、この語で検索すると証明が現れる。今回は高校数学の範囲内での証明を読んだ。更にはYou Tube上でも証明は現れる。白板を用い講師が熱心に証明している。この方法だと、理解しづらい箇所では画面を一時stopし、熟慮しながら証明を読むことも可能だ。You Tube上での証明は今風だ。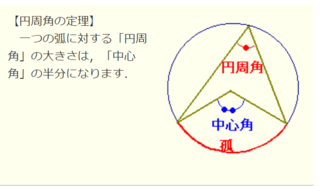

　えっ！(4)You Tubeでの証明をいろいろ見ていたら、「中学数学の範囲内での証明法」が現れた。三平方の定理(ピタゴラスの定理とも呼ばれる)と円周角の定理(円周角は中心角の半分という定理)のみで証明していた。無限に加えることは中学校では学ばないのでこれだけは中学数学のレベルを超えているが、それ以外は基本的には中学数学の範囲内での証明だった。2002年にある数学者が証明したそうだが、この証明には心底驚いた。興味のある方はYouTube上で“中学数学でバーゼル問題”で検索を。