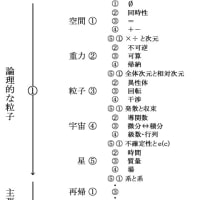
③粒子の⑤①を発散と収束にして、極限を扱ったみたいになったことで、④宇宙に微積が入るのは半ば必然であった。後になって気づいたことで、③粒子がフラクタルの要件であることから(フラクタルは仕組みの外にある成り行きとか状態とかパターンとかと思っていた)、宇宙を表しうる2大法則で③粒子と④宇宙が埋まるとなったことで、以降の見通しがだいぶんよくなってはいた。一般的に重要な宇宙の法則といえば相対性理論が思い浮かぶが、私はこれに疑問しか抱いていなかった。理解できないからというのもあるが、光速不変を前提としながら、その理由を示さないまま追究を諦めてしまった理論が、宇宙の根幹たりえるとは到底思えなかったからだ。とはいえ他にめぼしい理論もなく、相対性理論のすべてが否定されるわけではないのも確か。重力を空間の歪みとし、くぼむメッシュ状に表したのはアインシュタインの発明だと聞いたことがあるし、E=mc2なら重力のみで宇宙を表せるのではないかという示唆を含み、そう無碍にしきれるものではない。結局のところ⑤星に当てはめるしか残りの枠がないのと、そのままでは前後がつながらなくてどうしようもなかったので、逆に考えてみることにしたのがよかった。相対性理論が成り立つものとしておいて、だとすると宇宙には何があるのかと考えていく。我々の宇宙があって、相対性理論で導かれるような結果が起こる、と考えると理解できなくなるわけだが、逆に考えていくと、現宇宙論ではあるとみなされていて、どんなものかわかっているようでよくわからないものが、相対性理論の前提としていくつか出てきた。これが⑤星の中にうまくはまってくれた。まずは、④宇宙の②と③は微積の基礎からすぐに埋まった。②導関数:関数上の点が1次元下の導関数の性質を持つこと。関数を定義していないので、導関数が成り立つための条件がここに入るという考え方になる。③微分⇔積分:上位次元と下位次元の互換性。次に⑤星は相対性理論を参考にして、これも②と③がすぐに埋まった。②時間:相対論的な時間。時計を持ち込むわけにはいかないのでこれまで時間は想定しなかったが、通常の時間とは違うってことはわかる。③質量:重力でありエネルギーでもある。重力が量れないなら質量も量れないはずだが。いずれも相対性理論の結果として、常識とはかけ離れた振る舞いをする。計測が困難なのは共通で、以降の項目によっても定義されるものと見ておいたほうがいいという点を踏まえて、④場:一般相対性理論の重力場から。⑤系:特殊相対性理論の慣性系から。論の前提として出てくるのできちんと定義されているとは思うが、もちろんどんなものかよくわからない。こうして並べるとどれもどこか似通っている。(当面は、ちょうど④と⑤が埋まるという説得力のみを根拠とする。私にとってはこれだけで十分なのだが)現代物理学では、よくニュートン物理が通用しないという言い方がされる。新しいほうが上みたいに語られるのが通例で、ニュートン派の私としては、存在するものを成り立たせられない考えのほうが間違っていると思ったものだが。改めて考えてみると、どちらが間違いというよりかは、両パラダイムは表と裏の関係にあり、どちらかだけでは混沌としたままか固定化したままの世界になるのではないか。といったあたりで次の②主張する論理にうまくつながったものとみなし、話を⑤星の①に戻すと、これだけ相対性理論がはまると、その根本となるものがここに当てはまるような気がしてくる。つまり、光速不変の理由である。単純に考えると、時間を計るのにも、質量を量るのにも、基準となる単位が必要だったということになる。単位だから不変で計測されるのか、単位としてしか計算に用いないから不変なのか、他の基準を持ち得ないだけか、はひとまず置いておくとして、微積を調べていると、一つ基準になりそうなものがあって、ずっと気になっていて。が、その前に④宇宙の残り枠、④級数・行列:次元以外のものとの互換性。実数と自然数の関係もそうだが、繰り返しによって次元のように振舞うものに対しても、次元が互換性を保てること。⑤不確定性:微積の応用は多岐に渡ると言われているが、人類はまだその真髄を見ていないのではないか。世の中には便利な用語があるものだ。あらゆる性質、状態、計算が次元に内包されるとして、たとえば0になる性質と∞になる性質が相殺して、安定した性質が残るとしたら、相対性理論の基準にもなるのではないか?その候補としてe(ネイピア数)は、そういうものがあると思わせてくれるに足るものだとは言えまいか。基準のでき方としては、(相対性理論でネイピア数が何の意味もなさないかどうかにもよるが)A)eで安定して基準になったのか。B)安定したから基準(e)なのか。C)あるいは部分的安定の共通項として基準が現れるだけなのか。私としては、全宇宙で同じ基準と考えるのは危険と思うから、C寄りのBで、基準で計算するから不変、と考えたいところだが。もしかして、光が同じ速さで観測されるのは、eの微分係数を計算するかのような手順で光の速度を計っているからなのではないか?…やっと全部埋まった。