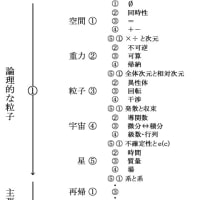
⑤①全体次元と相対次元:・全体次元:一般にイメージされる次元で、内容的にはヒルベルト空間に相当する。空間というと世界を覆っていると思いがちだが、世界に粒子が1つしかない場合、その粒子自体が世界であり、その粒子の可算という性質がとりうる状態が空間という見方ができる。 ・相対次元:粒子自体が次元を構成しているという見方。このうち0次元目が全体次元のような性質を持つので、相対次元と全体次元は表裏の関係にあるといえる。
・相対次元:粒子自体が次元を構成しているという見方。このうち0次元目が全体次元のような性質を持つので、相対次元と全体次元は表裏の関係にあるといえる。 粒子が可算という性質ゆえに他の粒子と影響し合うとしたら、どのように影響し合うかの性質が必要になるが、まずはそれぞれの性質が別々のものであることが前提となる。②異性体:粒子にも向きがいる。向きがあることで同じものが異性体として重ねられなくなると困るが、上位次元の中では解消されるし、そうしなくとも虚数のように反転しても解消される。③回転:可算の性質が結果として回転を示すならば、実際に回っている必要はない。こういった挙動は波動に似ているのかもしれない。とはいえ回転元と回転先はいりそうなので、次元には虚数も含まれているから、虚数方向に回転している、というのはどうだろうか?④干渉:磁場や熱のように粒子には力を伝える場や接点がいる。想定しているのは電子殻のようなもので、次元に起伏があるとは思えないので、回転しているなら干渉して虚数が絡んで…またもや虚数頼みだが、とにかく干渉縞のようなムラができれば他の粒子と干渉し合う境目になるのでは。⑤①発散と収束:際限なく干渉して発散すると、これを解消するために次元が上がり、上がった次元が重力として働き干渉の土台となる。干渉が収束すると、次元を下げる代わりに、下位次元粒子を生成して、収束が解消される。
粒子が可算という性質ゆえに他の粒子と影響し合うとしたら、どのように影響し合うかの性質が必要になるが、まずはそれぞれの性質が別々のものであることが前提となる。②異性体:粒子にも向きがいる。向きがあることで同じものが異性体として重ねられなくなると困るが、上位次元の中では解消されるし、そうしなくとも虚数のように反転しても解消される。③回転:可算の性質が結果として回転を示すならば、実際に回っている必要はない。こういった挙動は波動に似ているのかもしれない。とはいえ回転元と回転先はいりそうなので、次元には虚数も含まれているから、虚数方向に回転している、というのはどうだろうか?④干渉:磁場や熱のように粒子には力を伝える場や接点がいる。想定しているのは電子殻のようなもので、次元に起伏があるとは思えないので、回転しているなら干渉して虚数が絡んで…またもや虚数頼みだが、とにかく干渉縞のようなムラができれば他の粒子と干渉し合う境目になるのでは。⑤①発散と収束:際限なく干渉して発散すると、これを解消するために次元が上がり、上がった次元が重力として働き干渉の土台となる。干渉が収束すると、次元を下げる代わりに、下位次元粒子を生成して、収束が解消される。
次元がなぜ整数値をとるのか疑問に思っていた。 ⑤発散の次元が上がるというのは、段階的でありさえすればよく、便宜上整数を割り振れればよい。とはいえ計算は成り立たったほうがいいので、ある程度は規則的だとは思う。 下位次元粒子は、各次元粒子の位置関係と大きさと個数から、上位次元粒子から生成されるのは自明だと思っていたが、どうやって生成されるのかは想像もできなかった。 この考察で、重力よりも先に0次元目ができたという発想から、方々から用語を引っ張ってきて、うまく結びつけて、答えを導けたのではないか。