数学を学んだ多くの理論物理学者が物理学での研究や教育の場に就職する機会に恵まれず、経済学や神経科学などの領域で数学の能力を応用して活動していると聞いたことがある。
金融工学や神経情報科学はそうした人々が活躍して成立した巨大な学際科学だと言って良いだろう。
株の複雑な変動をコンピュータを使って予測する方法の開発に携わった人々の本が幾つも出版され、興味を持って読まれてきた。
沢山の神経繊維が織りなすネットワークの確率的活動として高次の精神活動をモデル化し、心理学を新しい力学で置き換えようとする試みも盛んに行われてきた。
しかし、残念ながら今度の金融不安は防げなかったし、反科学的精神療法は相変わらず衰えない。
20世紀を通じて量子力学を記述する数学の開発が行われ、それによって行われた計算は実験結果と嘗てない精度で一致し、僅かにズレが見いだされたときは更に新しい発見へ導いてきた。
それがどのような数学なのか。どのようにして計算するのか。
数学者の中には簡単なことですと言う人もいるが、実際には簡単に学べるものでないらしい。
推論の結果だけが、数学的説明を抜きにして、整理されて伝えられてくるようで、いつも違和感があった。
そこで強調される古典力学との違いは、第一に不確定性原理であり、量子の世界には「ゆらぎ」があることである。
日常的な時間・空間のスケールで成り立つ法則は、量子的時空のスケールでは必ずしも成り立たない、と。
しかし、日常的世界にも量子力学でのみ説明される現象が見られるし、科学と技術の進歩とともにそうした例を見ることが多くなっている。
極端に巨大なスケールと微小なスケールが一緒になっている現象としてブラック・ホールやビッグ・バンがある。
われわれの生活に直接関係ないようだが、宇宙の果てや時間の起源についての関心と理解は信心や迷信は言うまでもなく、生き方全般に深く関わっている。
一般相対性理論によればブラック・ホールを作っている物質は中心部の1点に圧縮されている。
その質量は途方もなく大きく、それでいてサイズは信じられないほど小さい。
大きな質量のために一般相対性理論を使い、小さいサイズのために量子力学を用いるが、2つの理論を合わせると方程式は破綻するのだとか。
ビッグ・バンも一般相対性理論と量子力学とが衝突する現象である。時間と空間が限りなく0に近かった創世の世界では、既に膨張して果てまで光も届かなくなっている宇宙が砂粒ほどの大きさに凝縮しており、まだ超高温度・超高密度だったとか。
その一般相対性理論と量子力学を統合するのが「超ひも理論」だ、と。
超ひも理論については何度もいろいろな機会に読んだが、その度に記憶が飛ぶのか、初めて読んだような気がする。
ブライアン・グリーン著 青木訳 2009
「宇宙を織りなすもの」12章:宇宙は“ひも”でできているか 草思社。
ひも理論は最初、強い核力を説明するものとして提案された。
強い核力は、2つの粒子を小さくて細いゴムのような“ひも”で繋ぐようにして生じていて、その量子力学的プロセスはオイラーのベータ関数で記述できる、と。
ひも理論の方程式は、高エネルギー衝突で、質量が0でスピンが2の沢山の粒子を生むと予測していたが、実験ではそのような粒子は発見されなかった。
やがて強い核力は量子色理論で説明されるようになった。
やがて、ひも理論が予測する粒子は重力子であって、方程式は核力ではなく、重力の量子力学的記述だ、と。
重力は他の力に較べて大変小さい。
“ひも”が伝達する力は、“ひも”が長いほど大きい。
従って重力を伝える“ひも”は大変短く、その存在は実験的に直接検証することは不可能だとする批判が強調される時期があった。
しかし、基本粒子を大きさが0の点状だと見なすと、方程式の解が無限大になり、実験事実に合わない場合が多い。
粒子は大きさが有限の“ひも”だとする理論によって全ての物質と力を統一的に記述する可能性が明らかになってきた、と。
時間と空間を分割してプランク長さとプランク時間になれば,宇宙を構成する最小要素に到達し、それ以上に分割することは意味を持たない。
プランクのスケールでは、時間間隔や空間距離を連続的な量だとする日常的な概念が通用しない。
液体としての水の温度の概念が、個々の水の分子については意味を持たないのと同じだ、と。
ひも理論によれば粒子の質量は振動する“ひも”のエネルギーである。
質量以外の電荷やスピンなどの性質も振動の特徴として捉えられる。
電子やクオークのスピンは整数でなく、1/2などの半整数であるり、半整数の振動パターンが現れるようにひも理論の方程式を導くと、振動パターンがペアになって現れ、そのスピンは0と1/2、1/2と1のように1/2だけ異なることが見いだされた。
整数スピンと半整数スピンとの関係は超対称性と呼ばれ、ひも理論は超対称性ひも理論、略して超ひも理論と呼ばれるようになった、と。
ブライアン・グリーンの解説で、ようやく超対称や超ひも理論の“超”を納得することが出来た。
もうひとつ呑み込めないでいたのは“超ひも”の空間次元が9次元だと云うことであった。2次元以上になれば面とか立体と呼ぶべきであって、追加した次元がどんなに小さくて、隠れるように“ひも”に纏わり付いていたとしても“ひも”と呼ぶのは適当ではないのではないか、と。
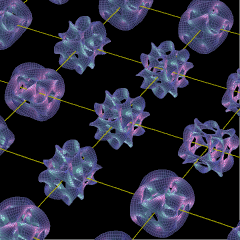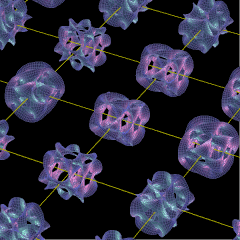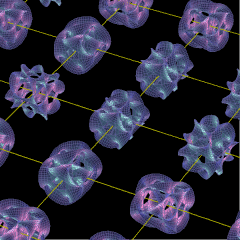
われわれの時間と空間についての日常的理解の中でイメージする“ひも”に追加され、隠れるようにして纏わり付いている6次元の極微の空間は、カリビとヤウという数学者によって提唱された多様体である、と。
Mathematicaというコンピュータ・ソフトの広告に載っているのがその例ではないかと思うが、金平糖のように凸凹し、かつ幾つか穴が開いていたりする図形である。
インターネットで検索すると動画で示したサイトがヒットする。
http://members.wri.com/jeffb/visualization/stringtheory.shtml
カントによれば、時間と空間の概念は先験的である、と。
しかし、幼児の発達過程を見れば、時間の概念がどのように形成されてくるか、コマ送りの画面を見るようにして捉えることが出来る。
自分の少年時代の空間知覚の記憶と現在の知覚像を比較すれば、空間がどのように歪むものが良く理解できる。
概念の個人的変動を捨象して共通理解を得られたとしても、スケールによって実体が全く異なってくることを忘れてはいけない。
それにしても、グリーンが指摘するように、ビッグ・バンの初期には9次元が等しく極微だった筈である。
宇宙が膨張し、冷却するにつれて、どうして4次元の時空だけが、現在のわれわれの経験的時空の概念になったのだろうか。
また新しい疑問である。
金融工学や神経情報科学はそうした人々が活躍して成立した巨大な学際科学だと言って良いだろう。
株の複雑な変動をコンピュータを使って予測する方法の開発に携わった人々の本が幾つも出版され、興味を持って読まれてきた。
沢山の神経繊維が織りなすネットワークの確率的活動として高次の精神活動をモデル化し、心理学を新しい力学で置き換えようとする試みも盛んに行われてきた。
しかし、残念ながら今度の金融不安は防げなかったし、反科学的精神療法は相変わらず衰えない。
20世紀を通じて量子力学を記述する数学の開発が行われ、それによって行われた計算は実験結果と嘗てない精度で一致し、僅かにズレが見いだされたときは更に新しい発見へ導いてきた。
それがどのような数学なのか。どのようにして計算するのか。
数学者の中には簡単なことですと言う人もいるが、実際には簡単に学べるものでないらしい。
推論の結果だけが、数学的説明を抜きにして、整理されて伝えられてくるようで、いつも違和感があった。
そこで強調される古典力学との違いは、第一に不確定性原理であり、量子の世界には「ゆらぎ」があることである。
日常的な時間・空間のスケールで成り立つ法則は、量子的時空のスケールでは必ずしも成り立たない、と。
しかし、日常的世界にも量子力学でのみ説明される現象が見られるし、科学と技術の進歩とともにそうした例を見ることが多くなっている。
極端に巨大なスケールと微小なスケールが一緒になっている現象としてブラック・ホールやビッグ・バンがある。
われわれの生活に直接関係ないようだが、宇宙の果てや時間の起源についての関心と理解は信心や迷信は言うまでもなく、生き方全般に深く関わっている。
一般相対性理論によればブラック・ホールを作っている物質は中心部の1点に圧縮されている。
その質量は途方もなく大きく、それでいてサイズは信じられないほど小さい。
大きな質量のために一般相対性理論を使い、小さいサイズのために量子力学を用いるが、2つの理論を合わせると方程式は破綻するのだとか。
ビッグ・バンも一般相対性理論と量子力学とが衝突する現象である。時間と空間が限りなく0に近かった創世の世界では、既に膨張して果てまで光も届かなくなっている宇宙が砂粒ほどの大きさに凝縮しており、まだ超高温度・超高密度だったとか。
その一般相対性理論と量子力学を統合するのが「超ひも理論」だ、と。
超ひも理論については何度もいろいろな機会に読んだが、その度に記憶が飛ぶのか、初めて読んだような気がする。
ブライアン・グリーン著 青木訳 2009
「宇宙を織りなすもの」12章:宇宙は“ひも”でできているか 草思社。
ひも理論は最初、強い核力を説明するものとして提案された。
強い核力は、2つの粒子を小さくて細いゴムのような“ひも”で繋ぐようにして生じていて、その量子力学的プロセスはオイラーのベータ関数で記述できる、と。
ひも理論の方程式は、高エネルギー衝突で、質量が0でスピンが2の沢山の粒子を生むと予測していたが、実験ではそのような粒子は発見されなかった。
やがて強い核力は量子色理論で説明されるようになった。
やがて、ひも理論が予測する粒子は重力子であって、方程式は核力ではなく、重力の量子力学的記述だ、と。
重力は他の力に較べて大変小さい。
“ひも”が伝達する力は、“ひも”が長いほど大きい。
従って重力を伝える“ひも”は大変短く、その存在は実験的に直接検証することは不可能だとする批判が強調される時期があった。
しかし、基本粒子を大きさが0の点状だと見なすと、方程式の解が無限大になり、実験事実に合わない場合が多い。
粒子は大きさが有限の“ひも”だとする理論によって全ての物質と力を統一的に記述する可能性が明らかになってきた、と。
時間と空間を分割してプランク長さとプランク時間になれば,宇宙を構成する最小要素に到達し、それ以上に分割することは意味を持たない。
プランクのスケールでは、時間間隔や空間距離を連続的な量だとする日常的な概念が通用しない。
液体としての水の温度の概念が、個々の水の分子については意味を持たないのと同じだ、と。
ひも理論によれば粒子の質量は振動する“ひも”のエネルギーである。
質量以外の電荷やスピンなどの性質も振動の特徴として捉えられる。
電子やクオークのスピンは整数でなく、1/2などの半整数であるり、半整数の振動パターンが現れるようにひも理論の方程式を導くと、振動パターンがペアになって現れ、そのスピンは0と1/2、1/2と1のように1/2だけ異なることが見いだされた。
整数スピンと半整数スピンとの関係は超対称性と呼ばれ、ひも理論は超対称性ひも理論、略して超ひも理論と呼ばれるようになった、と。
ブライアン・グリーンの解説で、ようやく超対称や超ひも理論の“超”を納得することが出来た。
もうひとつ呑み込めないでいたのは“超ひも”の空間次元が9次元だと云うことであった。2次元以上になれば面とか立体と呼ぶべきであって、追加した次元がどんなに小さくて、隠れるように“ひも”に纏わり付いていたとしても“ひも”と呼ぶのは適当ではないのではないか、と。
われわれの時間と空間についての日常的理解の中でイメージする“ひも”に追加され、隠れるようにして纏わり付いている6次元の極微の空間は、カリビとヤウという数学者によって提唱された多様体である、と。
Mathematicaというコンピュータ・ソフトの広告に載っているのがその例ではないかと思うが、金平糖のように凸凹し、かつ幾つか穴が開いていたりする図形である。
インターネットで検索すると動画で示したサイトがヒットする。
http://members.wri.com/jeffb/visualization/stringtheory.shtml
カントによれば、時間と空間の概念は先験的である、と。
しかし、幼児の発達過程を見れば、時間の概念がどのように形成されてくるか、コマ送りの画面を見るようにして捉えることが出来る。
自分の少年時代の空間知覚の記憶と現在の知覚像を比較すれば、空間がどのように歪むものが良く理解できる。
概念の個人的変動を捨象して共通理解を得られたとしても、スケールによって実体が全く異なってくることを忘れてはいけない。
それにしても、グリーンが指摘するように、ビッグ・バンの初期には9次元が等しく極微だった筈である。
宇宙が膨張し、冷却するにつれて、どうして4次元の時空だけが、現在のわれわれの経験的時空の概念になったのだろうか。
また新しい疑問である。




















※コメント投稿者のブログIDはブログ作成者のみに通知されます