算額(その861)
改訂版を参照のこと
山村善夫:現存 岩手の算額,昭和52年1月30日,熊谷印刷,盛岡市. http://www.wasan.jp/yamamura/yamamura.html
大円の一部である円弧内に正三角形2個と小円が入っている。正三角形の一辺の長さと小円の直径がわかっているときに大円の直径を求める術は如何に。
問では,「正三角形の一辺の長さと小円の直径がわかっているときに」とあるが,一般的にこの2つを任意に指定すると,図形を構成することは不可能である。正三角形の一辺の長さ,小円の直径,大円の直径の 3 変数のうち,1 つだけを指定して残りの 2 つのパラメータを決定するというのが妥当であろう。
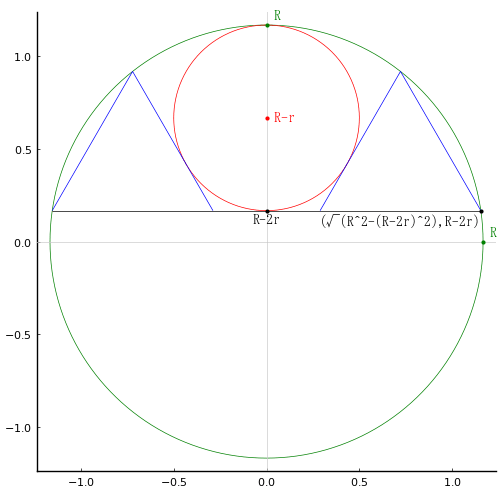
よって,以下のように定めて連立方程式を解く。
大円の半径と中心座標を R, (0, 0)
小円の半径と中心座標を r, (0, R -r)
正三角形の一辺の長さを a とする。
eq1 は小円の中心と正三角形の一辺までの距離が小円の半径に等しいこと,
eq2 は正三角形の頂点が大円の円周上にあることを意味している。
include("julia-source.txt");
using SymPy
@syms R::positive, r::positive, a::positive, x::positive
x = sqrt(R^2 - (R - 2r)^2)
eq1 = dist(x - a, R - 2r, x - a/2, R - 2r + a√Sym(3)/2, 0, R - r) - r^2
eq2 = (x - a/2)^2 + (R - 2r + a√Sym(3)/2)^2 - R^2
res = solve([eq1, eq2], (R, a));
2 組の解が得られるが,2 番目のものが適解である。
大円の半径は,小円の半径の 7/3,正三角形の一辺の長さは小円の半径の √3 倍である。
「術」は不適切である。
res[2]
(7*r/3, sqrt(3)*r)
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
r = 1//2
(R, a) = (7*r/3, sqrt(3)*r)
x = sqrt(R^2 - (R - 2r)^2)
plot()
circle(0, 0, R, :green)
circle(0, R - r, r)
plot!([x - a, x - a/2, x], R - 2r .+ [0, √3a/2, 0], color=:blue, lw=0.5)
plot!(-[x - a, x - a/2, x], R - 2r .+ [0, √3a/2, 0], color=:blue, lw=0.5)
segment(-x, R - 2r, x, R - 2r, :black)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(R, 0, " R", :green, :left, :bottom, delta=delta/2)
point(0, R, " R", :green, :left, :bottom, delta=delta/2)
point(0, R - 2r, "R-2r", :black, :center, delta=-delta/2)
point(0, R - r, " R-r", :red, :left, :vcenter)
point(sqrt(R^2 - (R - 2r)^2), R - 2r, "(√(R^2-(R-2r)^2),R-2r)", :black, :right, delta=-delta/2)
end
end;




























