ぐるぐる曼荼羅

ぐるぐる曼荼羅

締め切りが 2018/02/25 10:00 ＡＭ なので，その 1 分後に投稿されるように予約

【概要】
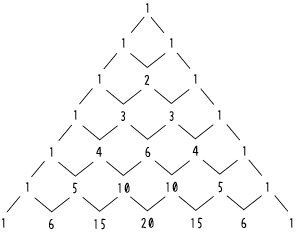
下図のように、正の整数が全て並んでいます。

数をひとつ指定しますので、その数のマスの上下左右に隣接しているマスの数を、昇順にコンマ区切りで出力してください。

【入力】
入力は標準入力から来ます。
35
のように、普通に10進数です。

【出力】
入力で指定された数のマスの上下左右に隣接しているマスの数を、昇順にコンマ区切りで出力してください。

先ほどの入力の場合、
8,34,36,100,101
を出力すれば正解です。

【例】
入力が 35 のとき，出力は 8,34,36,100,101
入力が 43 のとき，出力は 11,42,44,119,120

【補足】
・ 不正な入力に対処する必要はありません。
・ 入力は、1以上 十兆(10000000000000)以下です。

==================================================

規則性を見つけ出すこと。
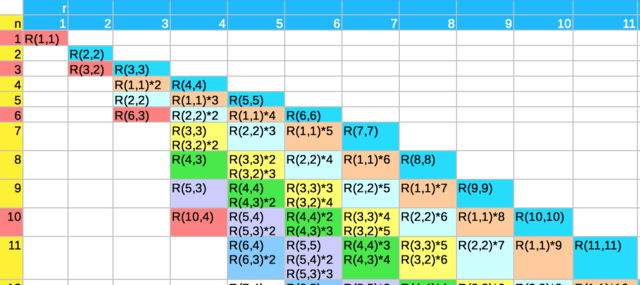
例えば，n = 35 の場合，n が含まれるレベルは小数部が 0 か 5，それより内側のレベルは小数部が 00, 25, 50, 75，外側のレベルは小数部なし（整数） とすれば，普通に配置できる（参照するときには，整数部のみを見ればよい）。

右下の隅に出てくる数（今の場合だと 7, 31, 91） は オンライン整数列大辞典の A068156 から導ける。
n が含まれるレベルにある数を x とすれば，内側のレベルに並んでいる数 z は z = x/2+定数1，外側のレベルに並んでいる数 y は y = x*2+定数2 の関係になっている。
n の前後は小数部が 0 の  n-1 と  n+1，外側に接するのは整数そのもの，内側に接するのは ｚ の整数部。
ワークシートを使っても簡単に答えを出せる。
解答先の R がバグっているのか，n = 10000000000000 のときだけ，cat(sort(unique(ans)), sep=",") ではだめで，cat(paste(sort(unique(ans)), collapse=",")) だと通る。見た目は同じなのに。
別の処理系（実行くん）でやると，"4999999999769, 9999..." のように，カンマの後に（他のカンマの後にはないのに，ここだけ）不可解な空白が入っている。わけわからん...

f = function(n) {
  ans = NULL
  if (n < 14) {
    a = matrix(c(49:40, 14, rep(13:10, each=2), 39, 15, rep(13:10, each=2), 38, 16,
      2, 2, rep(1, 4), 9, 9, 37, 17, 2, 2, rep(1, 4), 9, 9, 36, 18,
      3, 3, rep(1, 4), 8, 8, 35, 19, 3, 3, rep(1, 4), 8, 8, 34, 20,
      rep(4:7, each=2), 33, 21, rep(4:7, each=2), 32, 22:31), byrow=TRUE, ncol=10)
    index = which(a == n, arr.ind = TRUE)
    for (k in 1:nrow(index)) {
      i = index[k, 1]
      j = index[k, 2]
      ans = c(ans, a[i - 1, j], a[i + 1, j], a[i, j - 1], a[i, j + 1])
    }
    ans = ans[ans != n]
  } else {
    options(scipen = 100)
    mx = 0:44
    A068156 = 3 * 2 ^ mx + 0 ^ mx - 3
    e4 = cumsum(A068156 * 4) - 3
    e3 = e4 - A068156
    e2 = e3 - A068156
    e1 = e2 - A068156
    b1 = b2 = b3 = b4 = e1
    for (i in 3:length(e1)) {
      b1[i - 1] = e4[i - 2] + 1
      b2[i - 1] = e1[i - 1] + 1
      b3[i - 1] = e2[i - 1] + 1
      b4[i - 1] = e3[i - 1] + 1
    }
    lev = which(b1 <= n & n <= e4)
    m = e1[lev]-b1[lev]+1
    k = (n-b1[lev]) %/% m + 1
    if (n == b1[lev]) {
      ans = c(b1[lev]+1, e4[lev])
    } else if (n == e4[lev]) {
      ans = c(b1[lev], e4[lev]-1)
    } else {
      ans = c(n-1, n+1)
    }
    outer = 2*n+3*k+12*lev-15
    ans = c(ans, outer, outer+1)
    if (n %in% c(e1[lev], e2[lev], e3[lev])) {
      ans = c(ans, outer+3:4)
    } else if (n == e4[lev]) {
      ans = c(ans, n+1:2)
    }
    if (! n %in% c(e1[lev], e2[lev], e3[lev])) {
      if (n == b1[lev] || n == b1[lev]+1) {
        ans = c(ans, b1[lev]-1)
      } else {
        odd = k %% 2 == 1
        n2 = ifelse(odd == 1, n%/%2, (n-1)%/%2)
        inner = n2 + 14 - 1.5*k - 6*lev- 0.5*odd
        ans = c(ans, inner)
      }
    }
  }
  cat(sort(unique(ans)), sep=",")
}

#f(scan(file("stdin", "r")))

f(1) # 2,3,5,6,8,9,11,12
f(2) # 1  3 13 16 17
f(3) # 1  2  4 18 19
f(4) # 3  5 20 21 23 24
f(5) # 1  4  6 25 26
f(6) # 1  5  7 27 28
f(7) # 6  8 29 30 32 33
f(8) # 1  7  9 34 35
f(10) # 9 11 38 39 41 42
f(11) # 1 10 12 43 44
f(12) # 1 11 13 45 46
f(13) # 2 12 14 15 47 48
###
f(48) # 13  47  49 129 130
f(17) # 2 16 18 58 59
f(21) # 4 20 22 66 67
f(22) # 21 23 68 69 71 72
f(23) # 4 22 24 73 74
f(26) # 5 25 27 79 80
f(30) # 7 29 31 87 88
f(31) # 30 32 89 90 92 93
f(32) # 7 31 33 94 95
f(35) # 8  34  36 100 101
f(39) # 10  38  40 108 109
f(40) # 39  41 110 111 113 114
f(41) # 10  40  42 115 116
f(45) # 12  44  46 123 124
f(10000000000000) # 4999999999769,9999999999999,10000000000001,20000000000474,20000000000475

Python3 で書いてみたけど，くそったれ，だな。

処理系により indent が上手く扱えないとか，変なことが起きる。制御構文をインデントでという言語仕様は，百害あって一利なし。 { } でくくればいいじゃん。

Python で書くメリットは，全くない。

import numpy as np
 
def f(n):
  ans = []
  if n < 14:
    a = np.array([
      [49, 48, 47, 46, 45, 44, 43, 42, 41, 40],
      [14, 13, 13, 12, 12, 11, 11, 10, 10, 39],
      [15, 13, 13, 12, 12, 11, 11, 10, 10, 38],
      [16,  2,  2,  1,  1,  1,  1,  9,  9, 37],
      [17,  2,  2,  1,  1,  1,  1,  9,  9, 36],
      [18,  3,  3,  1,  1,  1,  1,  8,  8, 35],
      [19,  3,  3,  1,  1,  1,  1,  8,  8, 34],
      [20,  4,  4,  5,  5,  6,  6,  7,  7, 33],
      [21,  4,  4,  5,  5,  6,  6,  7,  7, 32],
      [22, 23, 24, 25, 26, 27, 28, 29, 30, 31]])
    for i in range(10):
      for j in range(10):
        if a[i, j] == n:
          if i > 0 and a[i-1, j] != n:
            ans.append(a[i-1, j])
          if i < 9and a[i+1, j] != n:
            ans.append(a[i+1, j])
          if j > 0and a[i, j-1] != n:
            ans.append(a[i, j-1])
          if j < 9and a[i, j+1] != n:
            ans.append(a[i, j+1])
  else:
    mx = 45
    A068156 = np.zeros(mx)
    for i in range(45):
      A068156[i] = 3 * 2 ** i + 0 ** i - 3
    e4 = np.cumsum(A068156 * 4) - 3
    e3 = e4 - A068156
    e2 = e3 - A068156
    e1 = e2 - A068156
    b1 = np.zeros(mx)
    b2 = np.zeros(mx)
    b3 = np.zeros(mx)
    b4 = np.zeros(mx)
    for i in range(2, mx):
      b1[i - 1] = e4[i - 2] + 1
      b2[i - 1] = e1[i - 1] + 1
      b3[i - 1] = e2[i - 1] + 1
      b4[i - 1] = e3[i - 1] + 1
    for i in range(2, mx):
      if b1[i] <= n and n <= e4[i]:
        lev = i
        break
    m = e1[lev]-b1[lev]+1
    k = int((n-b1[lev]) / m + 1)
    if n == b1[lev]:
      ans.extend([b1[lev]+1, e4[lev]])
    elif n == e4[lev]:
      ans.extend([b1[lev], e4[lev]-1])
    else:
      ans.extend([n-1, n+1])
    outer = 2*n+3*k+12*lev-3
    ans.extend([outer, outer+1])
    if n == e1[lev] or n == e2[lev] or n == e3[lev]:
      ans.extend([outer+3, outer+4])
    elif n == e4[lev]:
      ans.extend([n+1, n+2])
    if n != e1[lev] and n != e2[lev] and n != e3[lev]:
      if n == b1[lev] or n == b1[lev]+1:
        ans.append(b1[lev]-1)
      else:
        odd = k % 2
        if odd == True:
          n2 = int(n/2)
        else:
          n2 = int((n-1)/2)
        inner = n2 + 8 - 1.5*k - 6*lev- 0.5*odd
        ans.append(inner)
  ans = np.sort(np.unique(ans))
  s = str(int(ans[0]))
  for i in range(1, len(ans)):
    s = s+","+str(int(ans[i]))
  print(s)

f(int(input()))

壊れたパスカルの三角形

壊れたパスカルの三角形

締め切りが 2018/02/21 10:00 AM なので，その 1 分後に投稿されるように予約

設問

【パスカルの三角形】


パスカルの三角形は、上記のように隣り合った数の和を下段に書くことで作ることができます。

【問題】
パスカルの三角形を作るとき、隣り合った数の和を下段に追加していきますが、一か所だけ差を計算してしまっています。
次の図では、4段目・左から3つ目の値が、2 - 1 = 1になっているので、そこから下の部分の数が通常のパスカルの三角形と異なっています。



このような、壊れてしまったパスカルの三角形の一番下の段が入力として与えられたとき、“何段目の”、“左から何番目”の値を求める際に差を計算してしまったのかを特定するプログラムを書いてください。
※「差」は、『大きい方の値から小さい方の値を引く』と考えてください。

【入力・出力】
入力データは1行目にパスカルの三角形の段数k、2行目にk個の整数値が半角スペース区切りで与えられます。
kは最大60です。
k個の整数値は、壊れたパスカルの三角形のk段目を表しています。

これらの値を読み込み、間違えた計算方法で計算してしまった部分（差を計算した部分）を特定し、その段数と左から数えて何番目に当たるかを半角スペース区切りで出力してください。

（例）
※上記の問題文の図を使った例になります。

<入力>

    1.    7
    2.    1 6 13 14 9 4 1

<出力>

    1.    4 3
==================================================

プログラムは簡単なのであるが，k = 60 のときに，32 ビット整数はおろか，64 ビット実数で表現できる整数でも精度が不足して，正しい解が求まらない。
k = 60 のとき，出現する最も大きな数値は 59132290782430712 であるが，これに 1 を足しても 59132290782430713 にはならない

> class(59132290782430712)
[1] "numeric"
> 59132290782430712+1
[1] 59132290782430712

R では gmp パッケージを使えば問題ない。

library(gmp)

f = function(s) {

  s = unlist(strsplit(s, " "))
  y = as.bigz(s)
  n = length(y)
  x = as.bigz(1)
  for (i in 2:n) {
    x = c(x, as.bigz(0))+c(as.bigz(0), x)
  }
  cat(sum(x == y)+1, which(x != y)[1], "\n")
}

しかし，整数で扱える範囲で計算する（10の10乗を法として計算する）ことで，問題は回避できる。

f = function(s) {
  s = gsub("\n", " ", s)
  s = unlist(strsplit(s, " "))
  y = NULL
  for (t in s) {
    m = nchar(t)
    y = c(y, as.numeric(substr(t, max(1, m-9), m))) # 1e10 を法とする数値として解釈
  }
  n = length(y)
  x = 1 # パスカルの三角形を作る
  for (i in 2:n) {
    x = (c(x, 0)+c(0, x)) %% 1e10 # 1e10 を法として計算
  }
  cat(sprintf("%d %d\n", sum(x == y)+1, which(x != y)[1])) # どのように違うかに基づいて答えを出す
}

# f(readLines(file("stdin", "r"))[-1])

x1 = "1 6 13 14 9 4 1"

x2 = "1 11 49 123 204 252 252 204 123 49 11 1"

x3 = "1 23 253 1771 8855 33649 100947 245157 490314 817190 1144066
1352078 1352078 1144066 817190 490314 245157 98667 29089 6575 1771
253 23 1"

x4 = "1 39 741 9119 81591 565197 3153503 14562537 56777028 189763772
550304436 1398372924 3139455436 6271204644 11213769996 18044494260
26247932190 34644933810 41615977590 45587202210 45587202210
41615977590 34644933810 26247932190 18044494260 11213769996
6271204644 3139455436 1398372924 550304436 189763772 56777028
14562537 3153503 565197 81591 9119 741 39 1"

x5 = "1 47 1142 18152 210516 1902124 13971440 85875832 450939170
2054407014 8217773916 29135877368 92263710084 262596771388
675248867776 1575580701224 3348108992719 6499270398125
11554258485614 18851684897584 28277527346376 39049918716424
49699896548176 58343356817424 63205303218876 63205303218876
58343356817424 49699896548176 39049918716424 28277527346376
18851684897584 11554258485616 6499270398159 3348108992991
1575580702584 675248872536 262596783764 92263734836 29135916264
8217822536 2054455634 450978066 85900584 13983816 1906884 211876
18424 1176 49 1"

x6 = "1 59 1711 32509 455126 5006386 45057474 341149446 2217471399
12565671261 62828356305 279871768995 1119487075980 4047376351620
13298522298180 39895566894540 109712808959985 277508869722315
647520696018735 1397281501935165 2794563003870330 5189902721473470
8964377427999630 14420954992868970 21631432489303455
30284005485024837 39602161018878633 48402641245296107
55317304280338408 59132290782430712 59132290782430712
55317304280338408 48402641245296107 39602161018878633
30284005485024837 21631432489303455 14420954992868970
8964377427999630 5189902707355366 2794562806216874
1397280217187701 647515557028879 277494737500211 109684544515777
39853170228228 13250068965252 4004979685308 1091222631772
265739546891 57689366449 11280923797 2019817943 327031342
45057474 5006386 455126 32509 1711 59 1"

f(x1) # 4 3
f(x2) # 5 3
f(x3) # 22 18
f(x4) # 7 4
f(x5) # 33 2
f(x6) # 46 39

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

Python では，Int64 なので問題ない。

>>> import scipy as sp
>>> a = sp.array([59132290782430712])
>>> a.dtype
dtype('int64')
>>> a
array([59132290782430712])
>>> a+1
array([59132290782430713]) 識別されている

def f(s):
  s = s.split()
  n = len(s)
  y = []
  for i in range(n):
    y.append(int(s[i]))
  #print(y)
  x = [1]
  for i in range(2, n+1):
    x1 = x+[0]
    x2 = [0]+x
    for i in range(len(x1)):
      x1[i] += x2[i]
    x = x1
  position = 0
  line = n+1
  for i in range(len(x)):
    if x[i] != y[i]:
      if position == 0:
        position = i+1
      line -= 1
  print(line, position)

# int(input()) # 読み飛ばし
# f(input())   # 文字列を引数として渡す

x1 = "1 6 13 14 9 4 1"
x6 = "1 59 1711 32509 455126 5006386 45057474 341149446 2217471399 12565671261 62828356305 279871768995 "\
"1119487075980 4047376351620 13298522298180 39895566894540 109712808959985 277508869722315 647520696018735 "\
"1397281501935165 2794563003870330 5189902721473470 8964377427999630 14420954992868970 21631432489303455 "\
"30284005485024837 39602161018878633 48402641245296107 55317304280338408 59132290782430712 59132290782430712 "\
"55317304280338408 48402641245296107 39602161018878633 30284005485024837 21631432489303455 14420954992868970 "\
"8964377427999630 5189902707355366 2794562806216874 1397280217187701 647515557028879 277494737500211 "\
"109684544515777 39853170228228 13250068965252 4004979685308 1091222631772 265739546891 57689366449 "\
"11280923797 2019817943 327031342 45057474 5006386 455126 32509 1711 59 1"
f(x1) # 4, 3
f(x6) # 46, 39

集合写真できれいに写る配置は何通り？

集合写真できれいに写る配置は何通り？

締め切りが 2018/02/20 10:00 AM なので，その 1 分後に投稿されるように予約

設問
みんなで集合写真を撮るときの並び方の配置を考えます。
人数が少なければ一列に並ぶこともありますが、横に長くなると図のように複数列に並ぶことがあります。

複数列に並ぶときは、互い違いに並ばないと全員の顔が見えないので、
前の人の間から顔が見えるように並びます。
また、隣の人とは間を空けずに並ぶものとし、後ろに行けば行くほど人数が少なくなるものとします。
標準入力から人数 n が与えられたとき、n人が並ぶときの並び方が何通りあるかを求め、
標準出力に出力してください。
（個人は区別せず、その配置だけを考えます。）
なお、n は 1≦n≦200を満たす整数とします。
例えば、n=6 のとき、以下の8通りがあります。

【入出力サンプル】
標準入力
6

標準出力
8
==================================================================

これは，整数列大辞典の A001524 であるが，そこに書いてあるアルゴリズムの説明が不完全（？）で，私には解を導くことができなかった。

n が小さい場合について，順次列挙していくと，規則性が浮かび上がった。
R(n,r) は，n 人を並べるとき，最下段が r 人になる並び方の総数
R(n1, n1)=1，R(1,1)=r(6,3)=R(10,4)=1 などの自明な解と，規則的な関係が見られる。

規則をプログラムしたものの，R ではいつものとおり計算時間オーバーなので（私のシステムでは制限時間内），Python 3 でやってみても，やはり時間オーバー。
全く同じものを「Python3 ではなくて，Python  だよ！」と，だましたら，パスした。なんだこりゃ。

R プログラム

f = function(N) {
  n = 200
  a = matrix(0, n, n)
  for (i in 1:n) {
    a[i, i] = 1
  }
  tri.max = 19
  tri = integer(tri.max)
  for (i in 1:tri.max) {
    x = i*(i+1)/2
    tri[i] = x
    a[x, i] = 1
  }
  a[4, 3] = 2
  a[5, 3] = 1
  a[5 ,4] = 3
  begin = 3
  for (i in 6:N) {
    begin = begin + (i %in% tri)
    end = i-1
    for (j in begin:end) {
      top = i-j
      temp = 0
      for (k in top:1) {
        mul = i-top-k
        if (mul > 0) {
          temp = temp+a[top, k] * mul
        }
      }
      #cat(i, j, "\n")
      a[i, j] = temp
    }
  }
  options(scipen=100)
  cat(sum(a[N,]))
}

# f(scan(file("stdin", "r")))

f(4) # 3
f(6) # 8
f(10) # 38
f(100) # 970174745
system.time(f(200)) # 56220326505673、0.126 s

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

Python プログラム

import scipy as sp

def f(N):
  n = 200
  a = sp.reshape(sp.zeros(n*n), (n, n))
  for i in range(n):
    a[i, i] = 1
  tri_max = 19
  tri = sp.zeros(tri_max)
  for i in range(1, tri_max+1):
    tri[i-1] = i*(i+1)/2 - 1
  for i in range(tri_max):
    a[tri[i], i] = 1
  a[3, 2] = 2
  a[4, 2] = 1
  a[4 ,3] = 3
  begin = 2
  for i in range(5, N):
    if i in tri:
      begin += 1
    end = i-1
    for j in range(begin, end+1):
      top = i-j-1
      x = 0
      for k in range(top, -1, -1):
        mul = i-top-k-1
        if mul > 0:
          x += a[top, k] * mul
      a[i, j] = x
  ans = 0
  for i in range(N):
    ans += a[N-1, i]
  print(int(ans))

f(int(input()))

#f(6) # 8
#f(4) # 3
#f(10) # 38
#f(100) # 970174745
#f(200) # 56220326505673 Python 3 より Python 2 が速い？ 0.91s

一流を見分けられるのは誰？

一流を見分けられるのは誰？

締め切りが 2018/02/18 10:00 AM なので，その 1 分後に投稿されるように予約

今日のTVでは芸能人に何が一流品かを当てさせてその人を格付けする番組が人気ですが、こういった順位付けするという処理は、検索エンジンやレコメンドシステムといった日常的に使われるサービスの中でも極めて重要な役割を担っています。

さて、こうした順位付け問題はどのように評価するのが良いでしょうか？
順位付けを行う側を”評価者”、順位付けされる側を”アイテム”と呼ぶとき、TV番組であれば一番のアイテムがどれかを当てればOKかもしれませんが、サービスで使われるプログラムはすべて、あるいは上位10件という風に複数のアイテムを順位付けしないといけません。

ここで、例えばアイテムが３つあったときに、１位と２位を間違えるプログラムよりも、２位と３位を間違えるプログラムの方がまだ望ましいのは自明でしょう。

こうした評価者を評価するための精度評価指標として様々なものが提案されているのですが、今回の設問ではDCG(Discounted Cumulative Gain)と呼ばれる指標を使ってみたいと思います。

本設問で求められるプログラムの前提条件は、以下の通りとなります。

標準入力から、各アイテムの評価値（数値が大きいほど、評価が高いことを示す）が、次のように評価者の人数分複数行送られる
（評価者1）　アイテム1の評価値 アイテム2の評価値 アイテム3の評価値 ...
（評価者2）　アイテム1の評価値 アイテム2の評価値 アイテム3の評価値 ...
このとき、アイテムの順位ではなく評価値（順位とは逆で数値が大きいほど、評価が高い）が与えられることにご注意ください。
・ 入力されるテキストの行番号を評価者の番号とみなす
・ 評価者の人数は、3人以上5人以下とする
・ アイテムの数は、3個以上5個以下とする
・ 評価値は1以上10以下の整数とし、その組み合わせは固定される
・ 評価値はアイテムごとに異なり、重複や欠落はないものとする
・ アイテムの順序は、真の評価値が高い順に並んでいることを前提とする
・ よって、最も望ましい評価値は5>3>1という風に単調減少する場合となる
・ DCG(Wikipediaへのリンク)をすべてのアイテムに適用して評価者の順位を求めること。
・ ここでrel iと称される関連度を示す変数にはアイテムiの評価値を、変数pにはアイテム数をそのまま用いること。
・ またDCGの求め方は複数提案されているが、最初に解説される下記の数式を用いること

・ DCGの値が同じ評価者同士は、同じ順位とし、下の順位に合わせる。
例えば、評価者が3人で、上位2人が同じDCGの場合、2位が2名、3位が1名となる
・ 求めた順位を評価者の番号順に、改行区切りで標準出力に送ること

以下、入力と出力例です。

入力
3 1 2
1 3 2
3 2 1
出力
2
3
1

入力
6 10 3 1
10 3 1 6
10 3 6 1
10 3 6 1
出力
4
3
2
2

上記の１番目の例の場合、各評価者のDCGは、小数点第5位以下切捨てで、次のようになります。

3 + 1/log2(2+1) + 2/log2(2+2) = 4.6309
1 + 3/log2(2+1) + 2/log2(2+2) = 3.8927
3 + 2/log2(2+1) + 1/log2(2+2) = 4.7618

この数字が高いほど上位となるので、評価者の番号順に 2位 3位 1位となるわけですね。

いかがでしょうか？
一流だけを見分けるのか、一流以下のすべてを見分けるのかによって問題の複雑さがまるで変わってくることに気づかされますね。
本設問を通じて、検索エンジンやレコメンドシステムとサービスの裏側にも興味を持っていただければ幸いです。

【問題】
標準入力から、各アイテムの評価値（数値が大きいほど、評価が高いことを示す）が、評価者の人数分複数行送られます。
このとき評価されるアイテムの順序は、真の評価値が高い順に並んでいることを前提とした上で、順位付け問題の精度評価指標であるDCGを用いて各評価者の順位を求め、その結果を標準出力に返してください。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

設問が大げさな割りには，簡単に書けるプログラム

f = function(s) {
  x = sapply(s, function(t) as.integer(unlist(strsplit(t, " "))))
  n = nrow(x)
  y = 1/log2(1:n+1)
  z = apply(x, 2, function(a) sum(a*y))
  cat(sprintf("%d\n", rank(-z, ties.method="max")), sep="")
}

f(readLines(file("stdin", "r")))

「LCM・パレード」問題

「LCM・パレード」問題

締め切りが 2018/02/18 10:00 AM なので，その 1 分後に投稿されるように予約

自然数 a, b に対し、a と b の最小公倍数を LCM(a, b) と定義します。
例えば、LCM(6, 8)＝24 です。
 
さらに、自然数 n, k に対し、n 以下の全ての自然数 m に対する LCM(k, m)÷k の値の和を F(n, k)と定義します。
 
例えば F(9, 12)＝22 です。以下の表の最下列の数の和です。

同様に、F(10, 3)＝43, F(20, 9)＝162 となることが確かめられます。
 
標準入力から、自然数 n と k （1 ≦ n ≦ 10^8, 1 ≦ k ≦ 10^5）が半角空白区切りで与えられます。
標準出力に F(n, k) の値を出力するプログラムを書いてください。
 
 ===== ===== ===== ===== ===== =====

末尾に示す素直な R プログラムでは，n が大きくなると計算時間が掛かりすぎる。

なぜわざわざ LCM(k, n)/k なんて使うのだ？というところに実はヒントがあるのだろう。
k = 50 のときの LCM(50, m)/50, m=1, 2, ..., 50 を書き出してみれば，以下のようになる。

つまり，和を求める数値 LCM(k, m)/k は，m が k の素因数で割り切れるときにはその値で割る（同じ素因数が複数個ある場合も同様に）。
これらの和をとったものが F(n, k) である。


この方針で R プログラムを書いても，さすがに n = 100000000 では時間制限にひっかかる。
C で書き直して OK となるが，R プログラムは簡潔。

divisor = function(n)    {
  for (i in 2:sqrt(n)) {
    if (n %% i == 0) {
      return(i)
    }
  }
  return(n)
}

f = function(n, k) {
  x = as.numeric(1:n)
  while (k > 1) {
    div = divisor(k)
    if (n >= div) {
      i = 1:(n %/% div)*div
      x[i] = ifelse(x[i] %% div == 0, x[i] / div, x[i])
    }
    k = k/div
  }
  options(scipen=100)
  cat(sum(x))
}

f(9, 12) # 22
f(40, 50) # 502
f(312, 41) # 47708
f(7122, 360) # 10778909
system.time(f(1234567, 17200)) # 414701577895, 0.318 s
system.time(f(98777, 98999)) # 4878497253, 0.001 s
system.time(f(100000000, 98765)) # 4199787396686968, 2.080 s


C プログラム

#include <stdio.h>
#include <stdlib.h>
#include <math.h>

int divisor(int n)    {
  for (int i = 2; sqrt(n) >= i; i++) {
    if (n%i == 0) {
      return i;
    }
  }
  return n;
}

double f(int n, int k) {
  int i;
  int x[n+1];
  for (i = 1; n >= i; i++) {
    x[i] = i;
  }
  while (k > 1) {
    int div = divisor(k);
    for (i =1; n / div >= i; i++) {
      int i2 = i*div;
      if (x[i2] % div == 0) {
        x[i2] /= div;
      }
    }
    k /= div;
  }
  double sum = 0;
  for (int i = 1; n >= i; i++) {
    sum += x[i];
  }
  return sum;
}

int main() {
  int n, k;
  scanf("%d %d", &n, &k);
  printf("%.0f\n", f(n, k));
  return 0;
}

簡単に書けるが，遅い R プログラム

LCM = function(m, n) {
  n0 = n
  while ((temp = n %% m) != 0) {
    n = m
    m = temp
  }
  n0/m
}

f = function(n, k) {
  sum = 0
  for (m in 1:n) {
    sum = sum+LCM(k, m)
  }
  options(scipen=100)
  cat(sum)
}

#arg = scan(file("stdin", "r"))
#f(arg[1], arg[2])

f(9, 12) # 22
#f(40, 50) # 502
#f(312, 41) # 47708
#f(7122, 360) # 10778909
#system.time(f(1234567, 17200)) # 414701577895, 2.831 s
#f(98777, 98999) # 4878497253
#system.time(f(100000000, 98765)) # 4199787396686968, 298.946 s

切手を切って！

切手を切って！

締め切りが 2018/02/14 10:00 ＡＭ なので，その 1 分後に投稿されるように予約

設問

次のような切手シートがあります。

この切手シートから、3枚の切手がつながったまま切り取る方法は、以下のように10通りあります。

【問題】
切手シートの、たて・よこ・切り取りたい枚数が与えられたとき、切り取り方の総数を求めてください。
たて・よこの枚数は、いずれも1～10枚、切り取りたい枚数は1～5枚を想定してください。

【入力】
次の書式で数値が与えられます。

●1行目に、データセットの件数nが書かれています。
●2行目以降のn行に、たての枚数・よこの枚数・切り取りたい切手の枚数が、半角スペースで区切られています。

----（例）----
2
2 3 2
2 3 3
----（例）----

【出力】
データセット毎に、改行区切りで切手の切り取り方が何通りあるかを出力してください。

----（例）----
7
10
----（例）----

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

たとえば，正方形のピース数が k で，外形の行数が 2，列数が 3 のものは，以下の 6 通りのパーツである。
そのパーツを ｍ × ｎ の枠内に配置する方法は (m-2+1)×(n-3+1)×k 通りある。

k ごとの外形行数・列数，パーツの種類は以下のようになっている。

        row         col         parts
k    外形行数    外形列数    パーツの種類
2       2           1             1
        1           2             1
3       3           1             1
        2           2             4
        1           3             1
4       4           1             1
        3           2             8
        2           2             1
        2           3             8
        1           4             1
5       5           1             1
        4           2             12
        3           2             6
        3           3             25
        2           3             6
        2           4             12
        1           5             1

Ｒ によれば，プログラムは非常に簡単に書ける。

f = function(m, n, k) {
  param = list(0,
    list(row=2:1, parts=c(1,1)),
    list(row=3:1, parts=c(1,4,1)),
    list(row=c(4, 3, 2, 2, 1), parts=c(1, 8, 1, 8, 1)),
    list(row=c(5, 4, 3, 3, 2, 2, 1), parts=c(1, 12, 6, 25, 6, 12, 1)))
  p = param[[k]]
  col = rev(p$row)
  ans = sum((m-p$row+1)*(n-col+1)*p$parts)
  cat(ans)
}

f(2, 3, 2) # 7
f(2, 3, 3) # 10
f(5, 5, 2) # 40
f(3, 4, 3) # 34
f(3, 4, 4) # 65
f(6, 7, 5) # 1282
f(100,100,5) # 606196

Python3 では

def f(m, n, k):
    param = list([
        [[2,1], [1,1]],
        [[3,2,1], [1,4,1]],
        [[4, 3, 2, 2, 1], [1, 8, 1, 8, 1]],
        [[5, 4, 3, 3, 2, 2, 1], [1, 12, 6, 25, 6, 12, 1]]])
    p = param[k-2]
    ans = 0
    length = len(p[0])
    for i in range(length):
        ans += (m-p[0][i]+1)*(n-p[0][length-1-i]+1)*p[1][i]
    print(ans)

なお，ピース数 k ごとに，外形が m×n のパーツが何種類あるかは，以下のプログラムで求めることができる。

check = function(x) {
  if (any(colSums(x) == 0, rowSums(x) == 0)) {
    return(FALSE)
  }
  m = nrow(x)
  n = ncol(x)
  z = matrix(0, m+2, n+2)
  z[1+1:m, 1+1:n] = x
  for (i in 1+1:m) {
    for (j in 1+1:n) {
      if (z[i, j] == 1) {
        z[i, j] = 2
        break
      }
    }
    if (z[i, j] == 2) {
      break
    }
  }
  repeat {
    replace = FALSE
    for (i in 1+1:m) {
      for (j in 1+1:n) {
        if (z[i, j] == 2) {
          if (z[i-1, j] == 1) {
            z[i-1, j] = 2
            replace = TRUE
          }
          if (z[i+1, j] == 1) {
            z[i+1, j] = 2
            replace = TRUE
          }
          if (z[i, j-1] == 1) {
            z[i, j-1] = 2
            replace = TRUE
          }
          if (z[i, j+1] == 1) {
            z[i, j+1] = 2
            replace = TRUE
          }
        }
      }
    }
    if (!replace) {
      break
    }
  }
  !any(z == 1)
}

g = function(m, n, k=6, vervose=FALSE) {
  library(e1071)
  b = bincombinations(m*n)
  s = rowSums(b)
  b = b[s == k, , drop=FALSE]
  count = 0
  for (i in 1:nrow(b)) {
    x = matrix(b[i, ], m, n)
    if (check(x)) {
      count = count+1
      if (vervose) {
        cat(count, "\n")
        print(x)
      }
    }
  }
  cat(count, "pattern(s)\n")
}

対応のあるデータを再現する方法

PCI手術は有効か？という奥村先生の記事であるが

テストデータの生成手順が若干甘いのではないか？

データ生成で，y1 と x1，y2 と x2 は対応のあるデータなので，単にそれぞれの平均値と標準偏差だけでは特定できない。
x1 と y1，x2 と y2 の相関係数を定めないといけない。
奥村先生のやり方では，d を通じて両者の相関係数が決定される。
ただし，set.seed の値を変える（2箇所同じにすること）と，d が変わり，相関係数も変わる。
d ではなく，相関係数そのものを指定することで，データが特定できる。
なお，t.test の p 値が 0.2 という制約があるので，r1 か r2 のどちらかを決めれば，もう一方は自動的に決まる。

そこで，以下のようなプログラムを書いた。

library(MASS) # mvrnorm

g = function(r1 = 0.75) { # r1 は PCL での cor(x1, y1)
  f = function(r2) {
    #  set.seed(180210) # 不要
    d1 = mvrnorm(n = 104, mu=c(0, 0), Sigma=matrix(c(1,r1,r1,1),2), empirical=TRUE)
    x1 = d1[, 1]
    y1 = d1[, 2]
    x1 = (x1 - mean(x1)) / sd(x1) * 178.7 + 528.0
    y1 = (y1 - mean(y1)) / sd(y1) * 178.7 + 556.4
    d2 = mvrnorm(n = 90, mu=c(0, 0), Sigma=matrix(c(1,r2,r2,1),2), empirical=TRUE)
    x2 = d2[, 1]
    y2 = d2[, 2]
    x2 = (x2 - mean(x2)) / sd(x2) * 195.0 + 490.0
    y2 = (y2 - mean(y2)) / sd(y2) * 190.9 + 501.8
    t.test(y1 - x1, y2 - x2)$p.value - 0.2
  }

  # グローバル変数として r1 が与えられたとき
  # t.test(y1 - x1, y2 - x2)$p.value = 0.2 となる r2 = cor(x2, y2) を求める
  r2 = uniroot(f, c(0.1, 0.99))$root

  #set.seed(180210) # 不要
  # 平均値（標準偏差）が 528.0(178.7) と 556.4(178.7) の 2 変数で，
  # 両者の相関係数が r1 となるデータ x1, y1 を生成
  d1 = mvrnorm(n = 104, mu=c(0, 0), Sigma=matrix(c(1,r1,r1,1),2), empirical=TRUE)
  x1 = d1[, 1]
  y1 = d1[, 2]
  x1 = x1 * 178.7 + 528.0
  y1 = y1 * 178.7 + 556.4
  # 平均値，標準偏差，相関係数
  cat(sprintf("x1 = %.1f(%.1f)  y1 = %.1f(%.1f)  r(x1, y1) = %.5f\n",
    mean(x1), sd(x1), mean(y1), sd(y1), cor(x1, y1)))
  # 平均値（標準偏差）が 490.0(195.0) と 501.8(190.9) の 2 変数で，
  # 両者の相関係数が r2 となるデータ x2, y2 を生成
  d2 = mvrnorm(n = 90, mu=c(0, 0), Sigma=matrix(c(1,r2,r2,1),2), empirical=TRUE)
  x2 = d2[, 1]
  y2 = d2[, 2]
  x2 = x2 * 195.0 + 490.0
  y2 = y2 * 190.9 + 501.8
  # 平均値，標準偏差，相関係数
  cat(sprintf("x2 = %.1f(%.1f)  y2 = %.1f(%.1f)  r(x2, y2) = %.5f\n",
    mean(x2), sd(x2), mean(y2), sd(y2), cor(x2, y2)))
  # 念のため，t 検定の p 値が　0.2 になることを確認
  cat(sprintf("t.test() p value = %.5f\n", t.test(y1 - x1, y2 - x2)$p.value))
  # 重回帰分析を行い，PCL とプラセボの係数の p 値を見る
  x = c(x1, x2)
  y = c(y1, y2)
  z = rep(1:0, c(104, 90))
  r = lm(y ~ x + z)
  cat(sprintf("    lm() p value = %.5f\n", summary(r)$coefficients[3, 4]))
}

g(0.75)
g(0.80)
g(0.90)
g(0.95)
g(0.97)
g(0.99)

実行結果は以下の通りであるが，まとめると，
・ x1, y1 の相関が大きい場合には，lm の p 値は小さくなる
・ 場合によっては，0.078 程度にまで小さくなる

> g(0.75)
x1 = 528.0(178.7)  y1 = 556.4(178.7)  r(x1, y1) = 0.75000
x2 = 490.0(195.0)  y2 = 501.8(190.9)  r(x2, y2) = 0.98524
t.test() p value = 0.19999
    lm() p value = 0.10001

> g(0.80)
x1 = 528.0(178.7)  y1 = 556.4(178.7)  r(x1, y1) = 0.80000
x2 = 490.0(195.0)  y2 = 501.8(190.9)  r(x2, y2) = 0.94750
t.test() p value = 0.20000
    lm() p value = 0.09625
> g(0.90)

x1 = 528.0(178.7)  y1 = 556.4(178.7)  r(x1, y1) = 0.90000
x2 = 490.0(195.0)  y2 = 501.8(190.9)  r(x2, y2) = 0.87319
t.test() p value = 0.20000
    lm() p value = 0.08751

> g(0.95)
x1 = 528.0(178.7)  y1 = 556.4(178.7)  r(x1, y1) = 0.95000
x2 = 490.0(195.0)  y2 = 501.8(190.9)  r(x2, y2) = 0.83660
t.test() p value = 0.20000
    lm() p value = 0.08245

> g(0.97)
x1 = 528.0(178.7)  y1 = 556.4(178.7)  r(x1, y1) = 0.97000
x2 = 490.0(195.0)  y2 = 501.8(190.9)  r(x2, y2) = 0.82208
t.test() p value = 0.20000
    lm() p value = 0.08029

> g(0.99)
x1 = 528.0(178.7)  y1 = 556.4(178.7)  r(x1, y1) = 0.99000
x2 = 490.0(195.0)  y2 = 501.8(190.9)  r(x2, y2) = 0.80761
t.test() p value = 0.20000
    lm() p value = 0.07804

2進化10進数の1の数

2進化10進数の1の数

締め切りが 2018/02/10 10:00 AM なので，その 1 分後に投稿されるように予約

コンピュータにおける数値の表現方式の一つに2進化10進数(BCD)があります。
これは、10進数の各桁をそのまま2進数に置き換えたものです。

例えば、42の場合、十の位の「4」を2進数で表して「0100」、一の位の「2」を2進数で表して「0010」なので、「0100 0010」となります。
（ここでは符号は考えないものとします。）

Nが与えられる時、N桁の整数を「2進数で表した時」と「2進化10進数で表した時」に、ビット列に含まれる「1」の数が等しいものがいくつあるかを求めてください。

例)
42は2進数では「101010」で3個、2進化10進数では「0100 0010」で2個なので対象外、
52は2進数では「110100」で3個、2進化10進数では「0101 0010」で3個なので対象です。

【入出力サンプル】

Input
2

Output
20

====================================

R には 整数を二進数に変換する intToBits があるので，以下のように簡単に書けるが，それでも 7 桁の整数を対象にすると 1 分以上かかる。Java で書くにしても，intToBits を実装すると実行時間 1 秒は切れない。

f = function(n) {
  bits = sapply(0:9, function(x) sum(intToBits(x) == 1))
  count = 0
  for (i in (10^(n-1)):(10^n-1)) {
    a = sum(bits[as.integer(unlist(strsplit(as.character(i), "")))+1])
    b = sum(intToBits(i) == 1)
    count = count + (a==b)
  }
  cat(count)
}

ある整数の二進表記に 1 が幾つ含まれるかは，オンライン整数列大辞典の A000120 である。これを使うと，前述のプログラムよりは速い。
Java で書き換えて，やっと 1 秒の壁をクリアできた。

# A002487 a(n+1) = (2*k+1)*a(n) - a(n-1) where k = floor(a(n-1)/a(n))
A002487 = function(n) {
  a = integer(n)
  a[1] = a[2] = 1
  for (i in 3:n) {
    k = floor(a[i-2]/a[i-1])
    a[i] = (2*k+1)*a[i-1]-a[i-2]
  }
  a
}
a = A002487(20)

# A007814
A007814 = function(n) {
  a = A002487(n+1)
  floor(head(a, -1)/a[-1])
}

# A000120
A000120 = function(n) {
  a = A007814(n)
  b = integer(n)
  b[1] = 1
  for (i in 2:n) {
    b[i] = b[i-1]+1-a[i-1]
  }
  b
}

f = function(n) {
  table = sapply(0:9, function(i) sum(intToBits(i) == 1))
  begin = 10^(n-1)
  end   = 10^n-1
  x = A000120(end)
  count = 0
  for (i in begin:end) {
    if (x[i] == sum(table[as.integer(unlist(strsplit(as.character(i), "")))+1])) {
      count = count+1
    }
  }
  cat(count)
}

f(2) # 20
f(3) # 200
system.time(f(4)) # 2054, 0.052 sec.
system.time(f(5)) # 13906, 0.600 sec.
system.time(f(6)) # 122756, 6.336 sec.
system.time(f(7)) # 1167892, 67.848 sec.

Java プログラム

import java.util.Scanner;

public class Main {

  public static void main(String[] args) {
    int n;
    if (false) {
      Scanner cin = new Scanner(System.in);
      String line;
      line = cin.nextLine();
      n = Integer.parseInt(line);      
      System.out.println(f(n));
    } else {
      System.out.println(f(2));
      System.out.println(f(3));
      System.out.println(f(4));
      System.out.println(f(5));
      System.out.println(f(6));
      long start = System.currentTimeMillis();
      System.out.println(f(7));
      long end = System.currentTimeMillis();
      System.out.println((end - start) + "ms");
    }
  }

  static void dump(int [] a) {
    for (int i = 0; i < a.length; i++) {
      System.out.print(a[i]+" ");
    }
    System.out.println();
  }

  static int [] a002487( int n) {
    int [] a = new int[n];
    a[0] = 0;
    a[1] = 1;
    for (int i = 2; i < n; i++) {
      int k = a[i-2]/a[i-1];
      a[i] = (2*k+1)*a[i-1]-a[i-2];
    }
    return a;
  }

  static int [] a007814( int n) {
    int [] a = a002487(n+1);
    int [] b = new int[n];
    for (int i = 0; i < n; i++) {
      b[i] = a[i]/a[i+1];
    }
    return b;
  }

  static int [] a000120(int n) {
    int [] a = a007814(n);
    int [] b = new int[n];
    b[0] = 0;
    for (int i = 1; i < n; i++) {
      b[i] = b[i-1]+1-a[i-1];
    }
    return b;
  }

  static int bitCount2(int i) {
    int count = 0;
    int [] bits = {0, 1, 1, 2, 1, 2, 2, 3, 1, 2};
    while (i > 0) {
      count += bits[i % 10];
      i = i / 10;
    }
    return count;
  }

  static int f(int n) {
    int begin = (int)Math.pow(10, n-1);
    int end   = (int)Math.pow(10, n);
    int [] a = a000120(end);
    int count = 0;
    for (int i = begin; i < end; i++) {
      if (bitCount2(i) == a[i]) {
        count++;
      }
    }
    return count;
  }
}

ヒット・アンド・ブロー

ヒット・アンド・ブロー

締め切りが 2018/02/07 10:00 AM なので，その 1 分後に投稿されるように予約

ヒット・アンド・ブローというゲームがあります。
出題者は、0000～9999の、4桁の数字の中から、秘密の答えを選びます。
解答者は、出題者が選んだ秘密の答えを予想し、答えます。
秘密の答えに対し、予想の答えがどのくらい正しいかを、出題者は解答者に次のヒントを与えます。

[1]数字と、数字の場所（桁）が共に合っている場合はヒット
[2]数字は合っているが、数字の場所が合っていない場合はブロー

たとえば、秘密の答えが1300で、解答者が1234と答えた場合、

1300
1234

最初の桁は完全に一致していますので1ヒット（ヒットの場合はブローのカウントを行いません）、次の桁は一致していませんが、その次の桁に3がありますので、'3'という数が含まれているということで1ブロー、つまりこの場合は、1ヒット・1ブローとなります。

また、同じ数が複数ある場合、たとえば秘密の答えが0111、予想の答えが1000と答えた場合、「1」は1ブロー、「0」も1ブローと考え、全体で2ブローとします。

秘密の答えと予想の答えがピッタリ同じになった場合は、4ヒットと答えることになります。

【問題】
秘密の答えと予想の答えが与えられたとき、適切にヒット・ブローのヒントを出すプログラムを書いてください。

【入力】
●1行目に、データの件数Nが書かれています。整数値(1≦N≦100)
●2行目以降のN行に、秘密の答えと予想の答えが、半角スペース区切りで書かれています

----（例）----
3
1300 1234
0004 1234
1234 1230
----（例）----

【出力】
秘密の答え・予想の答えのセット毎に、改行区切りでヒントを出力してください。
ヒットの場合は'H'、ブローの場合は'B'としてください。
ヒット・ブローがない場合でも、'0H'や'0B'のように出力してください。
また、出力順はヒットを先にしてください。つまり、'mHnB'のような形でということです。

----（例）----
1H1B
1H0B
3H0B
----（例）----

==============================

f = function(s) {
  junk = sapply(s[-1], function(t) {
    t = unlist(strsplit(t, ""))
    a = as.integer(t[1:4])
    b = as.integer(t[6:9])
    c = a == b
    hit = sum(c)
    a = a[!c]+1
    b = b[!c]+1
    x = matrix(0, 2, 10)
    for (i in seq_along(a)) {
      x[1, a[i]] = x[1, a[i]]+1
      x[2, b[i]] = x[2, b[i]]+1
    }
    blow = sum(apply(x, 2, min))
    cat(sprintf("%iH%iB\n", hit, blow))
  })
}
f(readLines(file("stdin", "r")))


入力例1        出力例1
3
1300 1234    1H1B
0004 1234    1H0B
1234 1230    3H0B

入力例1        出力例2
20          
2527 0794    0H1B
0001 3220    0H1B
2664 7963    1H0B
5910 4794    0H1B
4183 2695    0H0B
5773 3297    0H2B
2417 2174    1H3B
1529 6475    0H1B
7797 5917    1H1B
2407 1023    0H2B
6860 2460    2H0B
8289 6285    2H0B
5670 8997    0H1B
7800 8700    2H2B
6543 3456    0H4B
3510 1099    0H2B
1529 0529    3H0B
4201 4201    4H0B
9144 8994    1H1B
5528 6918    1H0B

==============================

Python3 によるプログラム

import numpy as np

def f(s):
    for i in range(len(s)):
        a, b = s[i].split()
        a2 = np.zeros(4)
        b2 = np.zeros(4)
        for j in range(4):
            a2[j] = a[j]
            b2[j] = b[j]
        c = a2 == b2
        hit = sum(c)
        a3 = np.zeros(10)
        b3 = np.zeros(10)
        for j in range(4):
            if not c[j]:
                a3[int(a2[j])] += 1
                b3[int(b2[j])] += 1
        blow = 0
        for j in range(10):
            blow += min(a3[j], b3[j])
        print("%dH%dB" % (hit, int(blow)))

n = int(input())
a = []
for i in range(n):
    a.append(input())
f(a)

同じ数を表示し続ける7セグメントディスプレイ

同じ数を表示し続ける7セグメントディスプレイ

締め切りが 2018/02/06 10:00 AM なので，その 1 分後に投稿されるように予約

7セグメントディスプレイは7箇所の点灯の有無で数字を表示します。

この7セグメントディスプレイを横に並べて数を表示したとき、点灯している場所を数え、各桁での個数の「積」を次に表示します。

例えば、「718」からスタートすると、「7」は3箇所、「1」は2箇所、「8」は7箇所が点灯しているので、
3×2×7=42を計算し、次に「42」を表示します。
また、「42」において、「4」は4箇所、「2」は5箇所が点灯しているので、4×5=20より次に「20」を表示します。
次に「20」において、「2」は5箇所、「0」は6箇所が点灯しているので、5×6=30より次に「30」を表示します。
さらに「30」において、「3」は5箇所、「0」は6箇所が点灯しているので、5×6=30より次に「30」を表示します。

つまり、「718」から始まると「718」→「42」→「20」→「30」→「30」→…というように「30」が続くようになります。
このとき、登場する数は「718」「42」「20」「30」の4種類だけです。

標準入力から整数 n が与えられたとき、上記の処理を行って過去に表示した数が再度表示されるまで探索したとき、
登場する数がいくつあるか求め、その数を標準出力に出力してください。
なお、n は符号なし32ビット整数型の範囲(0〜4,294,967,295)とします。

【入出力サンプル】
標準入力
718

標準出力
4

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

R だと，簡単に書ける

f = function(n) {
  segments = c(6, 2, 5, 5, 4, 5, 6, 3, 7, 6)
  stack = n
  repeat {
    n = prod(segments[as.integer(unlist(strsplit(as.character(n), "")))+1])
    if (n %in% stack) {
      break
    }
    stack = c(stack, n)
  }
  cat(length(stack))
}

# f(scan(file("stdin", "r")))

f(718) # 4
f(0) # 2
f(31) # 3
f(12345) # 8
f(4198723075) # 11

くたばれ Python

Python を使う輩の気が知れない

R を使うべし

根拠はたくさんある

展開図上の反対側

展開図上の反対側

締め切りが 2018/02/02 10:00 AM なので，その 1 分後に投稿されるように予約

マス目を6つ指定します。
6つのマス目を立方体の展開図として組み上げた場合に、最初の面の反対側がどの面になるのかを計算してください。

【入出力】
入力は
glkmnq
のようになっています。

区切り文字なしで、面を示すアルファベット（図を参照）が6つ並んでいます。

出力するのは、最初の面の反対側の面のアルファベットです。
glkmnq
に対応する出力は、下図の通り、g の反対側は q なので
q
になります。

ただし、
jotfkpやklmngi
のように、
入力が立方体の展開図をなしていない場合は
-
を出力してください。

【例】
入力　glkmnq　　出力　q

入力　klmngi　　出力　-

入力　jotfkp　　出力　-

入力　bcdhmr　　出力　d


【補足】
    •    不正な入力に対処する必要はありません。
    •    ひとつながりになっていない場合は、展開図にはなっていないと判断してください。

========================================================

f = function(s) {
    abnormal = function(mat) {
        if (any(colSums(mat != " ") == 5, rowSums(mat != " ") == 5)) { # 縦（横）に5個並んでいる
            return(TRUE)
        }
        for (i in 1:4) { # 2行2列がある
            for (j in 1:4) {
                if (mat[i,j] != " " && mat[i+1,j] != " " && mat[i,j+1] != " " && mat[i+1,j+1] != " ") {
                    return(TRUE)
                }
            }
        }
        return(FALSE)
    }
    check = function(xy, m, n) { # (i, j) に隣接する面を辿って裏側になるものがあるかチェック
        a = array(xy, dim=c(2, m, n))
        for (k in 1:n) {
            ok = TRUE
            for (l in 1:m) {
                x = i+a[1, l, k]
                y = j+a[2, l, k]
                if (x < 1 || x > 5 || y < 1 || y > 5) {
                    ok = FALSE
                    break
                } else if (mat[x, y] == " ") {
                    ok = FALSE
                    break
                }
            }
            if (ok) {
                return(list(ok = TRUE, result = mat[x, y]))
            }
        }
        return(list(ok=FALSE, result=""))
    }
    letters = letters[1:25]
    t = unlist(strsplit(s, ""))
    mat = matrix(ifelse(letters %in% t, letters, " "), 5, byrow=TRUE)
    if (abnormal(mat)) { # 不正な展開図
        cat("-")
    } else {
        pos = grep(t[1], letters)-1
        i = pos %/% 5+1
        j = pos %% 5+1
        # B*E の場合（縦横の4方向） E が裏側
        # B の後の (i,j) の増分
        xy2 = c(0,-1,0,-2, -1,0,-2,0, 0,1,0,2, 1,0,2,0)
        a = check(xy2, 2, 4)
        if (a$ok) {
            cat(a$result)
            invisible()
        }
        # B
        # **
        #  E の場合 （8方向）
        xy3 = c(0,-1,1,-1,1,-2,
                0,-1,-1,-1,-1,-2,
                -1,0,-1,-1,-2,-1,
                -1,0,-1,1,-2,1,
                0,1,-1,1,-1,2,
                0,1,1,1,1,2,
                1,0,1,1,2,1,
                1,0,1,-1,2,-1)
        a = check(xy3, 3, 8)
        if (a$ok) {
            cat(a$result)
            invisible()
        }
        # B
        # ***
        #   E の場合 （8方向）
        xy4 = c(0,-1,1,-1,2,-1,2,-2,
                0,-1,-1,-1,-2,-1,-2,-2,
                -1,0,-1,-1,-1,-2,-2,-2,
                -1,0,-1,1,-1,2,-2,2,
                0,1,-1,1,-2,1,-2,2,
                0,1,1,1,2,1,2,2,
                1,0,1,1,1,2,2,2,
                1,0,1,-1,1,-2,2,-2)
        a = check(xy4, 4, 8)
        if (a$ok) {
            cat(a$result)
            invisible()
        }
        # B
        # ****
        #    E の場合 （8方向）
        xy5 = c(0,-1,1,-1,2,-1,3,-1,3,-2,
                0,-1,-1,-1,-2,-1,-3,-1,-3,-2,
                -1,0,-1,-1,-1,-2,-1,-3,-2,-3,
                -1,0,-1,1,-1,2,-1,3,-2,3,
                0,1,-1,1,-2,1,-3,1,-3,2,
                0,1,1,1,2,1,3,1,3,2,
                1,0,1,1,1,2,1,3,2,3,
                1,0,1,-1,1,-2,1,-3,2,-3)
        a = check(xy5, 5, 8)
        if (a$ok) {
            cat(a$result)
            invisible()
        }
    }
}
# f(readLines(file("stdin", "r")))

f("ngmbah") # g
f("rdmgch") # h
f("imdsen") # s
f("nuqprs") # u
f("gmknlr") # r
f("jbhaci") # h
f("ijcmbh") # b
f("gmlnrf") # r
f("nagihb") # b
f("pwrtsq") # -
f("fgbach") # -
f("mihgsn") # -

画像から連結成分の数を求めよう

画像から連結成分の数を求めよう

締め切りが 2018/02/02 10:00 AM なので，その 1 分後に投稿されるように予約

あなたは食品メーカーに勤めており、画像認識で商品を検査することで業務を省力化するよう求められました。

画像認識はDeep Learningが得意とする分野ですが、まず「隗より始めよ」ということで、画像から物体の数を求めるプログラムの開発に着手することにしました。

本設問で求められるプログラムの前提条件は、以下の通りとなります。

・ 標準入力から、ドット(.)とゼロ(0)の２文字で構成された文字列が同文字数複数行送られる。
・ 入力は１文字を1ピクセル、1行分の文字列を横一列とした２値画像とみなす。
・ この時横軸、縦軸とも長さは4以上20以下とする。
・ ゼロ(0)が上下左右斜めの8方向に連結した領域（連結成分）の数を求め、その数を標準出力に返すこと。
・ なお領域外のピクセルは、ドット(.)とみなすこと。

【問題】
標準入力から、ドット(.)とゼロ(0)の２文字で構成された文字列が同文字数複数行送られます。
この入力を２値画像とみなし、ゼロが上下左右斜めの8方向に連結した領域（連結成分）の数を求め、その数を標準出力に返してください。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

20×20 だと，地道にやっても R でも楽勝

f = function(s) {
    count = 0
    n = length(s)
    a = matrix(0, n+2, n+2)
    r = 1:n+1
    a[r, r] = sapply(s, function(t) unlist(strsplit(t, "")))
    repeat {
        # 新しい「島」の一端（"0" のセル）を探す
        found = FALSE
        for (i in r) {
            for (j in r) {
                if (a[i, j] == "0") {
                    found = TRUE
                    count = count+1
                    a[i, j] = "*" # あったら "*" にする
                    break
                }
            }
            if (found) {
                break
            }
        }
        if (!found) {
            break # "0" が 1 つもなかった（全て処理済み）ならば，終わり
        }
        # 1 つでもあれば，「島」を拡張する
        si = c(-1, 0, 1, -1, 1, -1, 0, 1)
        sj = c(-1,-1,-1,  0, 0,  1, 1, 1)
        repeat {
            replace = FALSE
            for (i in r) {
                for (j in r) {
                    if (a[i, j] == "*") { # "*" のセルの八方に "0" があれば
                        for (k in 1:8) {
                            if (a[i+si[k], j+sj[k]] == "0") {
                                a[i+si[k], j+sj[k]] = "*" # "*" に置き換える
                                replace = TRUE # 置き換えがあったことを記録
                            }
                        }
                    }
                }
            }
            if (!replace) { # 置き換えがなかったら「島」の拡張は終了
                for (i in r) {
                    for (j in r) {
                        if (a[i, j] == "*") {
                            a[i, j] = "." # 処理済みの「島」は「島」でないようにする
                        }
                    }
                }
                break
            }
        }
    }
    cat(count)
}

#f(readLines(file("stdin", "r")))

f(readLines("dat1")) # 2
f(readLines("dat2")) # 5
f(readLines("dat3")) # 7

dat1

00....
......
..000.
.00.0.
..000.
......

dat2

0....00.
0000000.
........
...0000.
..0....0
...0000.
........
.0.0..0.

dat3

....................
..000000............
.0..0..0....000000..
.0.....0....0....0..
.0000000....0.0..0..
............0.0.....
....00000...0.00000.
...00.......0.......
...0................
...0................
...0.....000........
....00..0...00......
.......00.....0.....
....................
...........000000...
.........00......00.
........0....000..0.
........0........00.
.........0000000000.
....................