オブジェクトに名前を付けて，オブジェクトを返す。
マニュアルにもあるけど，関数の終わりで使うとよい。
func = function() {
x = 9
names(x) = "result"
x
}
の代わりに，
func = function() {
x = 9
setNames(x, "result")
}
中身が，
> setNames
function (object = nm, nm)
{
names(object) = nm
object
}
なので，気が抜けるけど。
http://abc-analytics.com/decision-on-a-abtest-from-smart-bear-blog
「ABテストと統計数字(A smart bearのblogから)」なんだけど...ひどい...
冒頭から，いきなり
> カイ二乗値が4より上の組み合わせ（A,Bの回数)を緑色にしてる。
> ちなみに、カイ二乗が自由度１で値が３の時、p値は0.92。4で0.97くらい？
おいおい，それは，p 値ではなく，上側確率だし，p 値は「ある値以上の値を取る確率」なんだから，pchisq(1, 1, lower.tail=FALSE) = 0.08326452
でしょうが。
> 自由度１のカイ二乗値が6.15の場合は、98-99%の有意水準になります。
むちゃくちゃですね。
なんか，データをとって，カイ二乗検定をやって，カイ二乗値=6.15で，自由度が1 なら，
pchisq(6.15, 1, lower.tail=FALSE)
[1] 0.01314121
です。有意水準 5% のもとで，両側検定をした結果は，以下のように述べられます。
カイ二乗検定の結果，カイ二乗値は 6.15（自由度 1）となり，有意確率（p 値）は 0.013 で，有意水準 5% のもとで有意である。
> 僕を含めた大部分の人は統計が苦手。だって直感じゃだめだから。そこで、英語で書かれたblogで良い記事を見つけたので、紹介します。
って，いいわけをすればいいわけじゃないのだ
この記事を，「参考になる」として，あげている人もいるのだから，被害はあなただけじゃない
http://blog.share-wis.com/?p=359
「誰でも簡単にA/Bテストが作れるOptimizelyを実際に使ってみた」なんだけど...
オンラインツールを使って A/B テストを実際にやってみた結果の図が掲示されている。
(1) B: 138/219 = 63.4%(±6.4%) と A: 108/186 = 58.1%(±7.1%)で 8.5% 増という結果になった
独立二標本の比率の差の検定は，以下のようになり，有意差があるとはいえない結果である。後述(4)は怪しいものだということが分かる。
「8.5% 増」というのは，(63.0 - 58.1)/58.1*100≒8.5 ということであろうが，数字のマジックというか，パーセントのパーセントを取るというのも結果をよく見せる詐欺的手法ではないか？パーセントの差は 4.9% なんだから。改善率でいうか改善度でいうかの違いで，かなり印象が違う。
(2) テスト人数を増やせば統計的有意性が出るようになるのではないかと期待して，テストを走らせ続けていたが，費用がかかるので，ここで止めた
図を見れば，終了直前当たりで A が増え始めたように見えるが，テスト期間の中頃以降はほぼ同じレベルで推移していることが分かる。つまり，A, B の母比率はほぼ終了時の値とみてよいということであろう。母比率が 138/219 と 108/186 のままで，A, B の分母の割合も 219:186 のままで，このテストが継続されると，いずれは「A，B に有意な差がある」という結果になるのは確かである。では，どれくらいになったら有意になるのか。数式を解いてもよいが，ちょいちょいとシミュレーションする方が速いのでやってみると，3.7 倍くらいのサンプルサイズになって，A: 516/818，B:403/695 でやっと「有意水準 5% のもとで，A，B に差がある」という結果になる。ずいぶんなサンプルサイズだこと！当然といえば当然で，4.9% 位の「差」を検出するにはそれくらいのサンプルサイズが必要ということである。比率の差の大きさを抜きにして(4)でいうような「100である程度有意性が確保される」は，全くのはったりである。そんなことを信じてはいけませんよということ。
テストを行う前から A，B の差を知ることはできないがテストを行ってしばらくたつと（図で表されてる真ん中以降で，比率がほぼ安定するあたりのこと），母比率の目安がつくので，その時点でパワー・アナリシスを行うことをお勧めする。検出力を 0.8 として，他はデフォルトで，以下のようになる。
> power.prop.test(p1=138/219, p2=108/186, power=0.8)
Two-sample comparison of proportions power calculation
n = 1529.815 <<<< ここここ！
p1 = 0.630137
p2 = 0.5806452
sig.level = 0.05
power = 0.8
alternative = two.sided
NOTE: n is number in *each* group <<<< ここここ！
驚くべきことに，片方ずつで 1530，両方ではその 2 倍だから 3060 のサンプルサイズが必要になるということである。コンバージョンは900前後ですよ。「え？，A: 516/818，B:403/695 でよかったんじゃないの？」ですって？現実は，そんな比例配分で事が済むわけではないので，パワー・アナリシスの方が正しいと見積もる方がよいと思いますね。
(3) あまり費用をかけずにテストを実行したい場合、統計的にある程度有意な結果が得られたらテストを止め、別のテスト開始する、というのが賢い使い方のようだ
そうともいえるし，そうでないともいえる。
純粋に統計学に従うと，とんでもなく時間と費用がかかるということが分かったら（分かるようにはしなくてはならない），さっさとケツまくって，逃げるに越したことはない。
(4) サービス提供会社は，「100コンバージョン/作成したページで統計的にある程度の有意性が確保される」と説明されている
これは，全くのウソ。クライエントを騙して金をむしり取ろうとする，悪徳商人だね。
まずは，A，B それぞれがどれくらいの割合なのかを何通りか試算して，パワー・アナリシスをやってみて，そのテストを実際にやるかどうか決めるとよい。
> power.prop.test(p1=0.5, p2=0.45, power=0.8)
n = 1564.672
> power.prop.test(p1=0.10, p2=0.05, power=0.8)
n = 434.432
> power.prop.test(p1=0.05, p2=0.04, power=0.8)
n = 6744.933
NOTE: n is number in *each* group
http://web-analytics-or-die.org/2011/08/how_to_interpret_abtest/
「A/Bテストの結果をどのように解釈するか？」だけど...
1. 「A/Bテストはどのくらいの期間、実施すれば良いのですか？」
> 期間は関係ありません、両パターン間に有意差が認められるまでです
> CVが各100件集まるくらいが目安です
パワーアナリシスをするべきですね。「有意差が認められるまで」ではなく「『事前に設定した差』を検出するのに必要なサンプルサイズになるまで」ですね。
2. Aパターン、BパターンのCVRが取りうる範囲がかなり被っていることがわかります。範囲が被っているということは、どちらのCVRの方が高くなるのかわからないということです
示された図が box and whisker なのが疑問だが，それはさておき，オーバーラップしていても，差があるという結果になるというのは，この下 2 つ目の記事を参照のこと。
3. ちなみに、区間推定を用いる場合、カイ二乗検定よりも検定力は落ちるはずです。つまり有意差が出にくくなります
ちょっと何を言っているのかわからない。
検定と推定は等価です。例えば，二群の比率の差の検定が有意である場合，二群の比率の差の信頼区間は0を含まない。逆も真。
4. Web アプリの結果がおかしい？
http://web-analytics-or-die.org/abtest/
ページに示されてる例は，30/1000, 35/1000 の例の区間推定値が何によって計算されたか不明
binom.test でも prop.test でもないようだ。
判明：p±1.96√（p(1-p)/n) なんですね。でも，その近似式はあまりよくない。prop.test で使っているのは，n/(n+Z^2)*(p+Z^2/(2n)±Zsqrt(p(1-p)/n+Z^2/(4n^2))) なので，よろしく。
http://web-analytics-or-die.org/abtest/ で
50/100, 35/100 の比較例を表示してみたが，
パターン 下限 確率 上限
オリジナル 40.2% 50% 59.8%
テストパターン 25.65% 35% 44.35%
（下限，上限の計算法はよしとしよう）
また，有意差はあるのに「有意差はありません。」となってしまうが？？？
数値を変えてやってみたところ，どうやら，「信頼区間が重ならない場合に，有意差がある」と判定しているようだ。
しかし，それが間違いなのは 2. で示したとおり。
> chisq.test(matrix(c(50, 50, 35, 65), 2))
Pearson's Chi-squared test with Yates' continuity correction
data: matrix(c(50, 50, 35, 65), 2)
X-squared = 4.0102, df = 1, p-value = 0.04522
> prop.test(c(50, 35), c(100, 100))
2-sample test for equality of proportions with continuity
correction
data: c(50, 35) out of c(100, 100)
X-squared = 4.0102, df = 1, p-value = 0.04522
http://hivecolor.com/id/102
「ABテストを検定する」だが...
1. 標本数が少ない時は、有意差があるのかを知るために検定が必要です
「標本数」という用語の使い方を間違えている。あなたが使っているコンテキストでは，「標本の大きさ」あるいは「サンプルサイズ」と言うべき。ABテストの状況では，「標本数は常に 2」なのだから。
R の，prop.test(c(x1, x2), c(n1, n2)) の結果の表示で，"2-sample test for equality of proportions" と出るでしょう。
なお，後の方に，「サンプルスウ」という用語が出てきますが，曖昧な用語ですね。実験なんかで「試料」のことをサンプルと呼ぶことがあるので，「試料の数」ということなら，サンプルスウはサンプルサイズ（標本の大きさ）を表すことにはなりますが。
2. χ^2分布表を見ると、自由度1の5%点は3.84です。1.0 < 3.84となり、偶然この結果になる確率が5%以上あるので
偶然この結果「およびそれより極端な結果」になる確率が
とか
偶然この結果以上に極端な結果になる確率が
という意味です。
「χ二乗値が3.84以上になる確率」が 5% なのですから。
> pchisq(3.84, df=1, lower.tail=FALSE)
[1] 0.05004352
「χ二乗値が1*以*上*になる確率」は
> pchisq(1, df=1, lower.tail=FALSE)
[1] 0.3173105
細かな違いだけど，間違えてはいけない。
3. エクセルでは、二項検定を一発で行う方法はないようです…(^^)
いいえ，できますよ。
=BINOM.DIST(10,25,0.5,2)*2
これは，母比率が 0.5 以外の場合は正しくないが，あなたの場合は母比率が 0.5 なので，これで正しい答 0.424356222 が出る。
4. どれくらいの期間ABテストを行う必要があるの？
> 現実的には一週間やって有意差がでないんならやめてもいい気がします
必要な「サンプルサイズ」に言及がありましたが，ちゃんとやるなら，「パワー・アナリシス」をする必要があるでしょう。そのためには，「どれくらいの差があったら，差があったと結論するか」を決める必要がありますね。そして，「そのためにはどれくらいのサンプルサイズが必要か」を［事前に」見積もればよいのです。
5. 曜日ごとに、Aが良い場合とBが良い場合があります。こういう時はどうすればいいの？
> ちゃんとやるなら、AとBの曜日合算平均値を計算して、標本平均の差の検定とかをやる
本当にちゃんとやるなら，A/B と 曜日の両方ををダミー変数として，重回帰分析をすればよいでしょう。
6. ABテストではなく、ABCテストになるとどうなるの？
> パターンが2パターンより多くなると多変量解析とかを使うことになります
そういうのは，「多変量解析」ではありませんよ。多変量解析というのは，重回帰分析や，主成分分析や，因子分析みたいなもの。
ABC なら，比率の差の検定なら「独立 3 群の比率の差の検定」
A，B，C のクリック数が等しいかということならば，多項検定（AB なら二項検定なんでしょう？）
> まずは2パターンずつ試していく
これは，検定の多重性があるので，それぞれの二項検定の p 値を 3C2=3倍する必要がありますね。
7. 複数のABテストを同時にやるとどうなるの？
> これまた多変量解析の出番になるのですが、上の質問の答えと同じです。
6 に同じ。多重比較をやる。
8. χ^2検定って二項検定とどう違うの？
> 微妙に違うんですが、今回のような単純なABテストを行うのであれば同じと思って大丈夫です。
χ二乗検定は，二項検定の「漸近近似検定」。二項検定は正確な p 値が得られる検定。
サンプルサイズが大きくなれば，近似の程度は改善されるので，正確な p 値に近づいていく（ただし，母比率が 0.5 でないような場合は違う）。
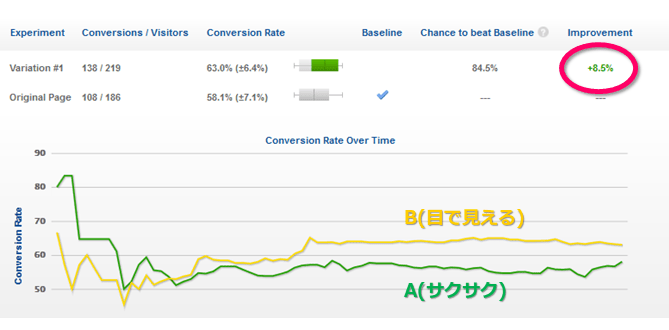
筆者が恥ずかしかったのか，今では非公開扱いになってしまって，ほかの人が閲覧できなくなっている。
で，
「ダイナマイト・プロットとはこのページにある最初のグラフのようなもの。」
というのが意味不明（参照不能）になっているので，「ダイナマイトプロットって何？」に答えておこう。
まあ，以下のようなもの。昔の漫画（若い人には分かるまい）のダイナマイトの点火装置（上のバー）を押すとダイナマイトが爆発するというような図である。こういうと，今の若い人にも「だせ〜〜〜〜」とわかるだろう。
というのが捕捉で，以下が当時の記事。
=============================================================================
http://abrahamcow.hatenablog.com/entry/2014/06/25/044107
「A/Bテスト、多変量テストの図示（Excel 版）」(非公開)なんだけど...
細かいけど，気になる所がたくさんあるので，メモしておく
1. 「多変量テスト」って
ページタイトルでも使われているわけですが，参照されている他の Web ページでも同じように使われているようですが，「2 群比較ではなくて多群比較（多重比較）」ということでは？
変量は 1 個でしょう？身長と体重と肺活量と 100 メートル走の成績というようなデータなら多変量データですけど。
ついでに，引用されている他の Web ページで「標本数が少ないABテストは...」，「標本数が多いABテストは...」と述べている所があるが，この文脈での「標本数」の使い方は間違いで，「標本の大きさ」，「サンプルサイズ」といわなければならない（この使い分けがちゃんとできていない人は，他でも間違いをおかしている可能性大）。
本来の「標本数」は文字通り標本の数であって，AB テストの場合は「独立 2 標本」だから標本数は 2，多群という場合は「標本数 > 2」のことを指す。
2. 「ダイナマイトプロット」は使わない
ダイナマイト・プロットとはこのページにある最初のグラフのようなもの。
じゃあ，他に何を使う？このページの 3 番目にあるようなグラフから折れ線を除いたもの。
ダイナマイトプロットの対象は，量的変数（の平均値と標準偏差または標準誤差）の場合が多い。しかし，そもそも，データは棒の中にあるのではない（棒グラフの根っこ当たりにはデータはないし，棒グラフの上辺の更に上にもデータはある。平均値±エラーバーは少なくともこの範囲におおくのデータが散らばっているよということを表している。
棒グラフは，本来は計数データの集計結果を示すもの。A 型が何人（何パーセント），B 型が何人（何パーセント）...というようなもの。棒の根っこの方も先端の方も同じ長さの部分を取ると人数（パーセント）は同じ。すなわち，この場合は棒グラフはデータの存在する範囲を表している。
計数データの集計結果でも，エラーバーを付けると意味が変わってくる。そのエラーバーは母数の信頼限界を表すので，棒は意味をなさない。
3. 「エラーバーが重なっていなければ母比率に有意差がある」はガセ
> n1 = n2 = 100
> x1 = 50
> x2 = 35
> prop.test(x1, n1)
1-sample proportions test without continuity correction
95 percent confidence interval:
0.4038315 0.5961685 <<< 母比率の信頼区間
> prop.test(x2, n2)
1-sample proportions test with continuity correction
95 percent confidence interval:
0.2591235 0.4525560 <<< 母比率の信頼区間
> prop.test(c(x1, x2), c(n1, n2))
2-sample test for equality of proportions with continuity
correction
95 percent confidence interval:
0.004563794 0.295436206 <<< 比率の差の信頼区間
「母比率に有意差があるかどうか」は各群の母比率の信頼区間ではなく（！），「母比率の差の信頼区間」であるため，図のように，前者が重なっていても，母比率に有意差ありという結果になることがある。
じゃあ，エラーバーなんか何の役に立つの？何の役にも立たない。かえって，誤解を植え付ける。百害あって一利なし。
図からエラーバーを取ったら...2つの点だけのグラフなんて...
4. 母比率の区間推定の計算法
どうも，R の計算結果とあわないなあと思っていたが，あまりよくない方の近似計算式 p±z*sqrt(p*(1-p)/n) を使っているようです（以下の conf1）。
この式は精度が悪い上に，0未満とか1より大きい値を計算してしまうので，ガードが必要になる。
prop.test などにはもう少しよい近似式を使っている（以下の conf2）。conf2 は，連続性の補正をしない場合の式なので，prop.test では correct=FALSE を指定する（correct=TRUE の場合と一致させることもできるが）。
conf = function(r, n, sig = 0.95) {
z = qnorm((1 - sig)/2, lower.tail = FALSE)
z2 = z^2
p = r/n
list(conf1 = p + c(-z, z) * sqrt(p * (1 - p)/n),
conf2 = n/(n + z2) * (p + z2/(2 * n) + c(-z, z) * sqrt(p * (1 - p)/n + z2/(4 * n^2))))
}
実行例
> conf(2, 51)
$conf1
[1] -0.01405716 0.09248853
$conf2
[1] 0.01082108 0.13216306
> prop.test(2, 51, correct = FALSE)$conf.int
[1] 0.01082108 0.13216306
attr(,"conf.level")
[1] 0.95
> conf(4, 58)
$conf1
[1] 0.003752698 0.134178337
$conf2
[1] 0.02714425 0.16433666
> prop.test(4, 58, correct = FALSE)$conf.int
[1] 0.02714425 0.16433666
attr(,"conf.level")
[1] 0.95
> conf(64, 3256)
$conf1
[1] 0.01488795 0.02442409
$conf2
[1] 0.01542330 0.02502083
> prop.test(64, 3256, correct = FALSE)$conf.int
[1] 0.01542330 0.02502083
attr(,"conf.level")
[1] 0.95
http://d.hatena.ne.jp/dichika/20140618/p1
「全角カッコの中にある全角数字を半角にして取り出したい」だが...
（ ）の中の数字は1文字という仕様なのかな？
数文字でもよいということにして，他のパッケージも使わずに，以下のようにすることもできる（警告メッセージが出るけど）。
as.numeric(chartr("０-９", "0-9", gsub("[（）]", "", gsub(".*(（[０-９]*?）).*", "\\1", smp))))
> smp = c("新しいファイル（１）","嫁", "ファイル（１２）は", "（その３）", "（１）と（２）")
> smp %>% zen2han() %>% str_extract("（\\d）") %>% str_replace_all("（|）","")
[1] "1" NA NA NA "1"
> as.numeric(chartr("０-９", "0-9", gsub("[（）]", "", gsub(".*(（[０-９]*?）).*", "\\1", smp))))
[1] 1 NA 12 NA 1
警告メッセージ:
強制変換により NA が生成されました
http://d.hatena.ne.jp/MikuHatsune/20140603/1401798802
「STAP細胞が見つかるまでひたすら適当な細胞を生成し続けるプログラム」なんだが...
> 重複を許してサンプリングしてて、26^4通りの細胞が論理的に考えられるなか、サンプリングの速度を適当に計算して作成にかかる時間の分布が取れるはずなので、やる気のある研究者というか当事者はやってみたらいいんじゃないかな(適当
> 時間がかかりすぎるので30回くらいやってみた。
これは，生起確率が 1/26^4 の，負の二項分布なので，真っ正直にシミュレーションしなくても rnbinom 関数で，負の二項分布に従う乱数が簡単に得られる。1000万個で3秒弱。
> system.time({
+ p = 1/26^4
+ k = 1
+ r = rnbinom(n=10000000, size=k, prob=p)
+ print(mean(r)) # 標本平均
+ print(k*(1-p)/p) # 母平均
+ print(var(r)) # 標本分散
+ print(k*(1-p)/p^2) # 母分散
+ })
[1] 456869.3
[1] 456975
[1] 208819732410
[1] 208826607600
ユーザ システム 経過
2.761 0.012 2.761
str_count 関数は，第1引数の文字列中に，第2引数の文字列が何回あるかを返す関数だということだが，第2引数の長さが1の場合には，strsplit を使って第1引数を1文字のベクトルにして比較演算をする方がはるかに速い。
library(stringr)
func1 = function(n0) {
count = 0
for (n in 1:n0) {
count = count+str_count(n, "7")
}
count
}
func2 = function(n0) {
count = 0
for (n in 1:n0) {
count = count+sum(unlist(strsplit(as.character(n), "")) == "7")
}
count
}
> n0 = 99999
> system.time(print(func1(n0)))
[1] 50000
ユーザ システム 経過
9.800 0.044 9.795
> system.time(print(func2(n0)))
[1] 50000
ユーザ システム 経過
0.684 0.003 0.683
> system.time(replicate(10000, str_count("67867899878786789999999999", "7")))
ユーザ システム 経過
0.910 0.004 0.939
> system.time(replicate(10000, sum(unlist(strsplit("67867899878786789999999999", "")) == "7")))
ユーザ システム 経過
0.079 0.002 0.095
