＞ 以前はGoogleアカウントの作成時に年齢入力は必要ありませんでしたが、いつからか必須になりまして、日本では現在、13歳未満のユーザーアカウントを作成することはできません。
＞ 子どもが13歳未満の場合はGmailを使えないので、“年齢制限”のない他のメールサービス（Yahoo！メールなど）を使う必要があります。
おお。馬鹿正直にもほどがあるぞ。年齢詐称しても，罰則規定はないだろう。悪用するわけじゃないのなら，へんな規約に従う必要はないだろう。
おお。馬鹿正直にもほどがあるぞ。年齢詐称しても，罰則規定はないだろう。悪用するわけじゃないのなら，へんな規約に従う必要はないだろう。
最近の，CM や映画（およびその予告編）などをみていて，喫煙シーン，飲酒シーンは，禁止すべきだと思う。
誤解されないように言えば，喫煙や飲酒を禁止すべきとは言っていないので。念のため。
> TOEFL を大学受験資格に 自民、首相に提言書
あほか。多くの，二流，三流大学は，定員割れになり，大学浪人が激増するだろうな。
法科大学院の経験を忘れるな。
現実を見よ！！と言いたいわ。藁
英語なんか，当たり前で，アメリカやイギリスには太刀打ちできないンだから，どうせなら，数学とか統計学のレベル保証でもすれば，インドには対抗できるんでは？
自民党の議員さん。あなた，ちゃんとアメリカやイギリスの議員さんと英語でやり合える自信があるの？（通訳を間においてもやり合えないというのはよく分かっているけど）。
統計学って知ってる？「理科」は？あなたたちのお得意？の「歴史」や「社会」，「政治」や［経済」なんかの文系科学は大丈夫？大学時代にちゃんと勉強した？
自分ができないことを他人に強制しちゃダメだよね。「反面教師にしてくれ」という意味なの？
45 ページの図。こんな図は派手だけど，困るなあ。
死亡者の数値を描いてある位置も恣意的だし。
二軸のグラフは二軸目の目盛りをどのように目盛るかでも印象が変わったりするし。
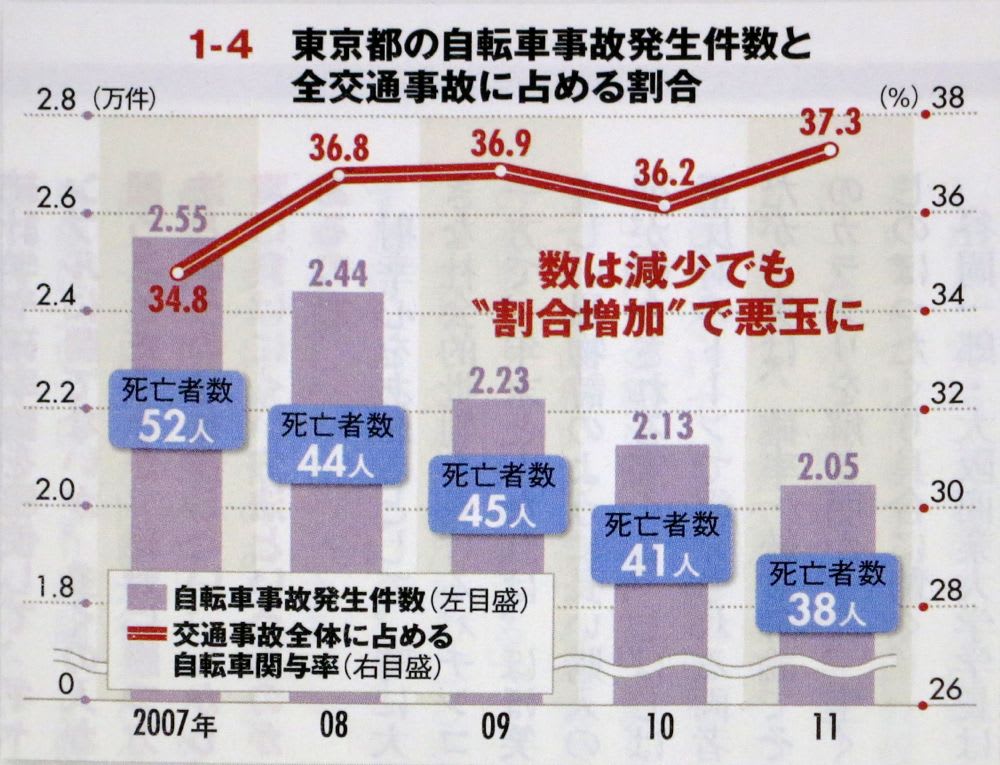
原点から始めてもらわないと。
統計！，統計！！というなら，ちゃんとやろうよね。
標準誤差
標準偏差（SD）とは，平均値に対する観測データのばらつきを表すが，標準誤差（SE）は，母集団の散らばりを表す。
---------
標準誤差についての説明は，全くのでたらめです。
標準誤差とは「母集団から標本を抽出し，標本（データ）の集計によって得られる統計量（標本平均とか，標本比率とかなんでも）のバラツキを表すもの。標本統計量の標準偏差を特に標準誤差という。例えば，標本平均の標準誤差は，「母分散/サンプルサイズ」の平方根である。」
対談者が「サンプリングの話でいうと，先ほど平均値と中央値の話をしましたが，『標準誤差』を一緒に把握しておく必要があります。平均点70点で標準誤差20点の人と，平均70点で標準誤差がほぼゼロという人ではまったく異なる人です。ただ，統計学を知らない人に説明する場合，標準誤差になるといきなり理解度が下がりますね。」と語っているのだが，そっくりそのままノシを付けてお返し申し上げたい。対談者がいっているのは，同じ能力を持つ人でも，発揮される能力にバラツキの大きい人と小さい人がいるというのだから，そのバラツキは，標準偏差のことである。
標準誤差が何の役に立つかと言えば，例えば，標本平均は母平均の推定値として使える（標本平均≒母平均）わけだけど，計算される標本平均は実際に母集団から抽出されるデータによって変わるし，データの大きさ（サンプルサイズ）によっても精度は変わる。
標本について言えば，母集団が正規分布に従うならば，標本平均±2×標本標準偏差の範囲には，標本のほぼ 95% が含まれることになる。
これと同じで，標本を抽出し標本平均を計算し，その標本平均を記録する。これを数万回繰り返し，その数万個の標本平均をデータと見なして標準偏差を計算するとその標準偏差が標準誤差にほぼ等しくなるだろう。そして，標本平均±2×標準誤差の範囲には95%くらいの標本平均が含まれるだろう。この区間を，母平均の信頼区間という。母平均の信頼区間は，このようなこと（標本抽出をして，標本に基づいて信頼区間を計算する）を繰り返すと，100回のうちほぼ95回は計算された信頼区間に母平均が含まれるということである。
標本平均で母平均を推定するのが点推定。
母平均を区間で推定するのが区間推定。
これと同じ考え方で，「標本統計量/標準誤差」の大きさで母数についての推測を行うのが，検定。
具体例
母平均値=0，母分散=1の正規分布に従う無限母集団から，標本の大きさ（サンプルサイズ）が 20 の標本を抽出する。標本平均を計算する。
これを，1000000 回行い，1000000 個の標本平均の平均値と標準偏差を求める。
> # このブログの都合で，代入記号に = を使う。よい子はまねしない。
> Means = colMeans(matrix(rnorm(20*1000000), 20))
> (m = mean(Means)) # 0 に近い値のはず
[1] -4.836502e-05
> (s = sd(Means)) # 1/sqrt(20) ≒ 0.2236068 に近い値のはず
[1] 0.2235299
> mean(Means = m+2*s) # 0.05 に近い値のはず
[1] 0.045334
クロス集計
与えられたデータのうち，複数の項目を掛け合わせてデータ分析を行うこと。クロスさせるデータに上限はないが，増えすぎるとサンプル数が減ってしまう。
-----
クロス集計というのは文字通り「集計」で，まだ「分析」までは行かないだろう。
「複数の項目を掛け合わせて」というのは，複数の変数を対象にして（クロスさせて）ということだろう。前に述べた「分割表」を一般的には「クロス集計表」と呼ぶ人が多い。
一番簡単なのは，二重クロス集計。二次元の度数分布表を作るということ。前に述べた，四分表は更に単純な場合（2行2列しかない）。行方向に一方の変数のカテゴリー（カテゴリー変数でない連続変数の場合はカテゴリー化して使用），列方向にもう一方の変数のカテゴリーをとり，それぞれのカテゴリーに該当するデータ数を数え，セルに記入する。期待値や行方向・列方向のパーセントを付けたりもする。
Excel のピボット関数（？）でも集計できるだろう。
二重クロス表の例
三重クロス表の例
「クロスさせるデータに上限はない」というのは，「クロスさせる変数の個数に上限はない」ということだろうか。3変数について3重クロスをすれば，3次元の度数分布表になるが，まあ，紙に印刷して提示するためには，二次元にして表示することになる。以下，n変数についてのn重クロスも同じことである。
あるいは，次とも関連するが，変数のカテゴリー数のことか？もともとカテゴリー数がほどほどのカテゴリー変数ならよいが，連続変数をカテゴリー化してクロス集計を使用として，階級幅を狭くする（結果として，カテゴリー数が大きくなる）とか，そもそもカテゴリー数が大きいと，集計結果が入る延べのセルの数が大きくなるので，必然的にセルあたりのデータ数が少なくなるというような，次の項のようなことが生じる。
「上限はないが，増えすぎるとサンプル数が減ってしまう」これは，集計表のセルに該当するデータの個数が少なくなってしまうということ。
「サンプル数」という言葉も微妙。
回帰式
ある変数と他の変数がどのように相関しているかの関係を把握する際に変数化し，数式化することを回帰分析という。その際の計算式が回帰式（y=ax+b）となる。この際の，a，b を回帰係数という。
-----
大きな間違いはないと言ってよいが，「変数化し」というのはどういうことか？既に前半で，「ある変数と他の変数が」と，変数を扱うことを前提にしているのに。
「数式化」というのも，どういう文脈で数式にするかをちゃんと書かないとね。その後で y=ax+b と出てくるのだけど，この説明だけで，x に重みを付けて（傾きを掛けて）切片を足すと予測される変数の予測値になるという，この式の意味は伝えられるのか？式自体は式の意味を伝えない。せめて出てくる変数（x, y など）が何を表すかを明示的に書かないと。
回帰分析とは「複数（最も単純には1個）の変数の重みつき合計値で別の1変数の値を予測すること。予測がうまくできるような重みを客観的に（データから）求めることである。」とでも。
念のため
シミュレーションなんかしないでも答は出るから
3つのドアの後ろに，ヤギ，ヤギ，自動車が隠されている。
プレーヤーは，どれか一つのドアを選ぶ。自動車のドアなら自動車がもらえる。
ここで，司会者は必ず，プレーヤーが選んだのではないドアを開けて，ヤギであると知らせる（答を知っているので，必ずヤギのいるドアを開ける）。
司会者はプレーヤーに，「ドアを選び直してもいいよ」と言う。
さて，プレーヤーは，最初のドアのままでよいというか，残りのドアに変えるか。
自動車をあてる確率が高いのはどちらの戦略か。
メタ・モンティホール問題 で，別のブログ中のプログラムが間違っていると指摘していた。
この問題は何回か読んでいたが，シミュレーションプログラムは書いたことがなかったので書いて見た。
意外と短く書けたので記録しておく。
MontyHallProblem <- function(ChangeAnswer=TRUE) {
door <- sample(c("景品", "ヤギ", "ヤギ")) # セット
Player <- sample(3, 1) # どれかを選ぶ
Monty <- setdiff(setdiff(1:3, Player), which(door=="景品"))[1] # 必ずヤギのドアを開ける
if (ChangeAnswer) { # 最初の答を変えるなら
Player <- setdiff(setdiff(1:3, Player), Monty)
}
return(door[Player] == "景品") # 当たったかどうか結果を返す
}
> mean(replicate(100000, MontyHallProblem()))
[1] 0.66588
> mean(replicate(100000, MontyHallProblem(FALSE)))
[1] 0.33387
確かに，司会者の助言に従って，ドアを変える方が倍も確率が高いのだなあと，実感。
P値（ピーち）
Probability（確率）の略。実際には何の差もないのに，誤差や偶然によって差が生じる確率のことをいう。P値が大きければ，偶然でも起こりうると考えられ，小さければ（慣例的には5%以下），偶然には起こりそうにないレベルの差と考えられる。
検定
100%正しい訳ではないが，95%以上正しいのでおおむね正しいと考えて問題ないという推測統計の考え方を応用し，真意の疑わしい主張や仮説に対して，論理的・統計的な否定を行うこと。その否定を数多く繰り返すことで，否定されない仮説が積み上がり，真理に近づくという考え。
-------
P値は，英語でも p-value と略され，それを直訳して「P値」として使われている。確かに P は probability の略ではあるが P値=probability でないことは明らか。単に 「probability」 ではないし，「確率」でもない。「●●の確率」ということで，「●●」が厳密に定義されている。だから probability という一般名称ではなく，特別な名前（専門用語）「p-value」になっているのだ。
「実際には何の差もないのに，誤差や偶然によって差が生じる確率のことをいう」は不正確すぎる。「実際には何の差もないのに」というのは，「差がないという帰無仮説のもとでは」ということだろう。「誤差や偶然によって差が生じる確率」というのは何を指しているのか？正確に述べれば，「差がないという帰無仮説のもとで，観察された事象以上に極端な事象が生じる確率」のことである。だからこそ，この値（確率）が小さければ，「そんな小さな確率でしか観察されない事象が実際に観察された。本当は，帰無仮説が間違えている（差がある）と考えた方がよい（帰無仮説を棄却する）と判断する」のである。素人に説明するときに帰無仮説だの，観察された事象以上に極端な事象が生じる確率だのいうのがいやなんだろうけど，曖昧にするときりがない。
「100%正しい訳ではないが，95%以上正しいのでおおむね正しいと考えて問題ない」言っていることがよくわからない。信頼区間の信頼率や，「1-第一種の過誤」を言っているのだろうが，それらは「95%以上正しい」とか「おおむね正しい」とか「正しいと考えて問題ない」などというものとは本質的に違う。
「真意の疑わしい主張」って，何だろう？「真偽の疑わしい主張」か？
検定は，「論理的・統計的な否定を行うこと」ではない。「帰無仮説を棄却する」ことは検定の 1 つの結論だが，「帰無仮説が棄却できない」というのも，もう一つの結論だ。「否定」することだけではない。
「否定を数多く繰り返すことで，否定されない仮説が積み上がり，真理に近づく」というのは，科学的なものの考え方であって，検定はその一つの方法・アプローチであろう。
検定とは，「平均値に差がない，相関関係がないなどの仮説（帰無仮説）が正しいとしたときに，実際に観察されたデータに基づいて計算される平均値の差，相関係数などの数値以上の結果（統計量）が得られる確率（P値）を求め，その確率が小さい（慣例的には5%が採用されることが多い）ときに，平均値に差がある，相関関係があるなど，帰無仮説を否定する仮説（対立仮説）を採択するという推論過程。P値が大きいときには，帰無仮説を保留する。」とでも。
本文中にも，対談者が，「『偶然にすぎない確率が何パーセント』という検定の考え方」とか「検定を行えば『偶然そうなった可能性が5%以下なので，暫定的に正しいと考えてよいだろう』といえます」と（微）妙なことを言っている。
記事の下部に対談中に出てきた用語解説というのがあるが，簡潔に書いたつもりかもしれないが曖昧だったり間違っていたりがはなはだしい。対談者のどちらかが書いたのか？記者・編集者が書いたのだろうか？対談者はチェックしなかったのか？
四分割表
二つ以上の変数の関係性を分析するための表。この表で分析する手法をクロス分析という。
普通は「四分表」という。英語では fourfold table 。つまり，2行2列（2 by 2 = 4）のクロス集計表。
2行2列もふくめ，それより大きいクロス集計表は，「n x m 分割表」，英語では contingency table と呼ぶ。
二つの変数（二つ以上の変数ではない）について集計したもの。3つ以上の変数を対象にすることもあるが，それらはもはや四分表などとは呼ばれない。単に集計表と総称されるだろう。
対象とされる変数はカテゴリー変数に限らず，連続変数を階級分け（カテゴリー化）したものも含む。集計結果は行方向または列方向の合計が 100% になるようにパーセントを付けることもある。そのパーセントを見ただけでも，二つの変数の関係がわかる。しかし，もっとも一般的には「カイ二乗検定（このような名前は不適切らしいが）」を行い，二つの変数間の関係が統計学的に意味のあるものかどうかを判定する。このようなのを「クロス分析」とは言わない。
なお，例としてあげられているのは「スノウの分析」で，これは，水源と死亡者数の2変数の関係を表してはいるが，本来の四分表ではない。
四分表の例としてあげるなら，本文中にもある例を出せばよいのに。
やせた やせなかった 合計
ダイエット薬飲んだ 70人 30人 100人
ダイエット薬飲まなかった 20人 80人 100人
合計 90人 110人 200人
> 特集記事が『最強の武器「統計学」』ということで巷で話題になっている週刊ダイヤモンドを買って読んでみたが，まあ，細かくいえば突っ込みどころが多いものであった。西内・飯田対談などは，一般向けにはあれくらいラフに言い切ってしまう方がいいのかもしれないが
実際はそんな生やさしい評価ではなく，とんでもないいい加減な記事になってしまっているのではないか？
用語解説だけでもいい加減。（「よい」加減じゃないよ）
続報，乞うご期待？
PVアクセスランキング にほんブログ村
